数据结构与算法分析 - 6 - 散列
1.散列表
描述:通过适当的散列函数在词条的关键码与向量单元的秩之间建立起映射关系的数据结构,也叫哈希表。
完美散列:在时间和空间性能上都达到最优的散列。
散列的查找和删除:根据散列函数可以在O(1)的时间里确定要查找/删除的关键码在散列函数中的地址。
空间利用率:散列表的查找和删除可以在时间复杂度O(1)下实现,但当散列规模很大时,其空间利用率将变得很低。
类比词典,尽管词典中的所有词条都有可能出现,但实际需要的词条数目远远小于总词条的数目,此时向量的装填因子就会很小。
(装填因子已在数据结构与算法分析 - 3 - 向量ADT中提到过)
此时就需要合理得设计散列函数,使得散列可以兼顾时间和空间上的效率。
2.散列函数
一组词条在散列表中的具体分部取决于散列方案,即词条与桶地址之间的映射关系。
hash() : key → hash(key)
hash()即为散列函数。key为关键码,hash(key)为关键码对应的散列地址。
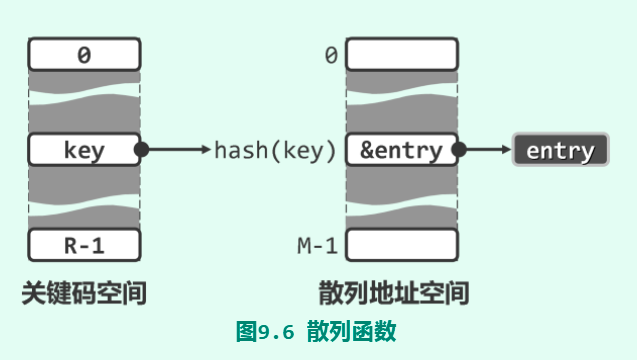
散列冲突(hash冲突):出于提高空间利用率的目的,散列函数不可能为单射,因此不同的关键码映射到同一个散列地址中(即散列冲突)是不可避免的。
散列函数的设计原则:
(1)不能过于复杂,保证散列地址的计算能够在O(1)的时间里完成。
(2)关键码映射得到的散列地址应该尽可能地覆盖整个散列地址空间,充分利用。hash()最好是满射。
(3)关键码映射到散列中各桶的概率应该尽可能接近1/M(M为散列中桶的数量),即关键码经映射得到的地址应该尽可能地均匀分布在散列中,避免极端低效。
除余法:hash(key) = key mod M
为减小散列冲突的概率,M一般取素数,可有效避免大量关键码聚集在同一个桶中。
MAD法(multiply-add-divide methed):素数除余法尽管可以有效降低散列冲突的概率,但散列地址仍具有一定的连续性,由此得到的散列表中,原本相邻的关键码的散列地址依然相邻,且较小的关键码的散列地址大多数集中在散列表前面。最关键的是,0除余结果永远是0,其散列地址将始终为0。为弥补素数除余法在连续性上的不足,可以将散列函数改写。
hash(key) = (a * key + b) mod M,M为素数,a>0,b>0,且a mod M ≠ 0
这样改写以后,相邻的关键码得到的散列地址之间将产生空桶,原先的不动点0也被消除了。
其实原本的素数除余法可以看作这种方法的特殊情况,即a=1,b=0时,此时a,b都没有起到实质性作用。
伪随机数法:好的散列函数要求随机性和无规律性,这与生成随机数的思路不谋而合。
hash(key) = rand(key) mod M
使用该散列函数的缺陷是,不同环境中的随机数发生器并不相同,可移植性并不好。
数字分析法:从关键码的特定进制展开中取出特定的若干位构成一个整数地址。
例如,hash(123456789) = 123456789 = 13579 取十进制展开的奇数位。
平方取中法:将关键码平方取中间三位数。
例如,hash(123) = 15129 = 512
折叠法:将关键码分割成为若干段,再累加起来。
例如,hash(123456789) = 123 + 456 + 789 = 1368
异或法:将关键码的二进制展开分割成等宽的若干串,进行异或运算得到散列地址。
hash(411) = hash(110011011) = 110 ˆ 011 ˆ 011 = 110 = 6
3.解决散列冲突
1)分离链接法
多槽位:多槽位的思路很简单,即一桶多槽。
在一个桶中设立多个槽位,发生冲突的关键码放在同一个桶中的不同槽位中。
多槽位的缺陷是,预先不知道有多少关键码会发生冲突,设置的槽位过少会引起溢出,而过多则造成空间利用上的浪费。
独立链法(链接法):多槽位法缺陷产生的根源是数组大小固定,那么用链表替换数组,可以很好解决这一问题。
如下图就是用独立链法生成的散列表。
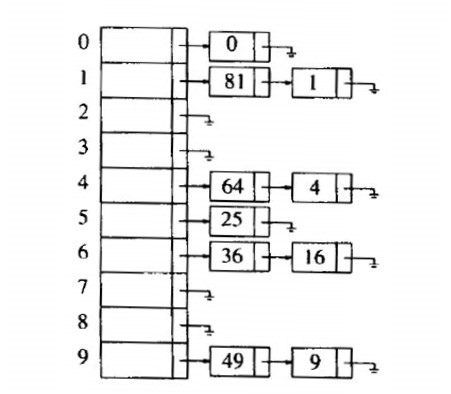
分离链接法的散列表声明:
1 struct ListNode; 2 typedef struct ListNode *Position; 3 struct HashTbl; 4 typedef struct HashTbl *HashTable; 5 6 HashTable InitializeTable(int TableSize); 7 void DestroyTable(HashTable H); 8 Position Find(ElementType Key,HashTable H); 9 void Insert(ElementType Key,HashTable H); 10 ElementType Retrieve(Position P); 11 12 struct ListNode 13 { 14 ElementType Element; 15 Position Next; 16 }; 17 18 typedef Position List; 19 20 struct HashTbl 21 { 22 int TableSize; 23 List *TheLists; 24 };
寻找素数:(可制作素数表)确定散列表大小(除余法)
1 int IsPrime(int num) 2 { 3 if(num == 1) return 0; 4 int i; 5 for(i = 2; i <= sqrt(num); i++) 6 if(num%i == 0) 7 return 0; 8 return 1; 9 } 10 11 int NextPrime(int TableSize) 12 { 13 int i; 14 for(i = TableSize; i < INT_MAX; i++) 15 if(IsPrime(i)) 16 return i; 17 return 0; 18 }
散列函数:仍然采用除余法
1 int Hash(const ElementType Key,int TableSize) 2 { 3 return Key%TableSize; 4 }
初始化:(C语言实现)
1 HashTable InitializeTable(int TableSize) 2 { 3 HashTable H; 4 int i; 5 if( TableSize < MinTableSize ) 6 { 7 Error("Table size too small"); 8 return NULL; 9 } 10 11 /*Allocate table*/ 12 H = malloc(sizeof(struct HashTbl)); 13 if(H == NULL) 14 FatalError("Out of space!!!"); 15 16 H->TableSize = NextPrime(TableSize); 17 18 /*Allocate array of lists*/ 19 H->TheLists = malloc(sizeof(List)*H->TableSize ); 20 if(H->TheLists == NULL) 21 FatalError("Out of space!!!"); 22 23 /* Allocate list headers */ 24 for(i = 0; i < H->TableSize; i++) 25 { 26 H->TheLists[i] = malloc(sizeof(struct ListNode)); 27 if(H->TheLists[i] == NULL) 28 FatalError("Out of space!!!"); 29 else 30 H->TheLists[i]->Next = NULL; 31 } 32 return H; 33 }
查找:查找发生冲突的关键码时,时间复杂度将大于O(1)
1 Position Find(ElementType Key,HashTable H) 2 { 3 Position P; 4 List L; 5 L = H->TheLists[Hash(Key,H->TableSize)]; 6 P = L->Next; 7 //只有查找到有冲突的关键码时才查找链表 8 while( P != NULL && P->Element != Key ) 9 P = P->Next; 10 return P; 11 }
插入:
1 void Insert(ElementType Key,HashTable H) 2 { 3 Position Pos,NewCell; 4 List L; 5 Pos = Find(Key,H); 6 if(Pos == NULL) 7 { 8 NewCell = malloc(sizeof(struct ListNode)); 9 if(NewCell == NULL) 10 FatalError("Out of space!!!"); 11 else 12 { 13 L = H->TheLists[Hash(Key,H->TableSize)]; 14 NewCell->Next = L->Next; 15 NewCell->Element = Key; 16 L->Next = NewCell; 17 } 18 } 19 }
删除:分离链接法实现的散列表删除操作很简单,和链表的删除操作一样。
独立链的缺点是,相对于数组中连续的存储空间,链表存储元素的物理空间是不连续的,使用指针为元素分配地址需要时间,这样进行查找时将产生额外的开销。
公共溢出区:思路很简单,实现也不难。在原散列之外另设一个独立的词典,凡是发生冲突的关键码都将被映射到该公共溢出区中。
查找时,如遇到发生冲突的关键码,则再到公共溢出区中查找一次即可。
2)开放定址法(闭散列策略)
开放定址:之前的三种方法都倾向于将发生冲突的关键码分离出来(多槽位,引入次级结构链表,设置溢出区),而每个关键码只能进入其应该进入的桶中。
而开方定址法则倾向于就地解决冲突问题,当关键码应该进入的桶中已经有了元素时,就尝试选择散列中另外的桶单元,在这个前提下,散列中所有的桶单元都是对所有关键码开放的,因此叫作开放定址。
尝试选择另外的桶单元的方法有多种。
线性探测法:沿线性方向尝试选择其他桶单元,遇到空桶则放入其中。
线性探测是很容易想到的,既然这个桶已经被占用,那么就近找一个空桶放置(体现为遍历散列表)无疑是很简便的。
然而,随着散列规模的变大,每次线性探测的时间将变得越来越长,因为冲突发生时通过线性探测填满的空桶将有可能引起更多的冲突(想象连环追尾),这些冲突得到的单元会很快聚集起来形成区块,使线性探测的效率急剧下降,这就是聚集现象。这将导致即使散列表中还有相当大的空间,每次线性探测也要经过多次尝试才能找到空桶。
例如,构造一个长度为5(取素数)的散列表,要插入的元素是{0,1,2,3,5},散列函数就采用普通的除余法。
当按照0,1,2,3,5的顺序进行插入时,前四个元素都很顺利地进入了桶中,只有最后一个元素需要进行尝试。这样的效率可以接受。
| 0 | 1 | 2 | 3 | 4 |
| 0 | 1 | 2 | 3 | 5 |
然而当按照5,0,1,2,3的顺序插入时,效率将截然不同。
首先插入5,很好地插入到了地址为0的桶中。
| 0 | 1 | 2 | 3 | 4 |
| 5 |
接下来插入0,应该放在地址为0的桶中,而线性探测发现,该桶已经被占用,所以向后移动一格,发现地址为1的桶为空,放进去。
| 0 | 1 | 2 | 3 | 4 |
| 5 | 0 |
不难发现,依照此顺序继续插入,5后面的所有元素都需要进行尝试,这些单元很快聚集在一起,导致后面的几乎所有元素都要进行多次尝试。
当散列表规模较大时,效率会变得很低。因此,试探的方法需要改进。
平方探测法:类似于设计散列函数优化除余法时的思路,MAD法也可以用在这里缓解聚集现象。MAD法得到的单元之间间隔为常数。采用平方探测法可以使间隔随着探测次数的增加以平方速率增长。
(hash(key) + j²) mod M j = 0,1,2...
j为进行试探的次数。
平方探测法适用于大规模的散列,此时规模已经达到可以忽略其可能会破坏数据局部性的副作用。
双散列:使用两个散列函数,当尝试失败时,在距离hash2(key)的地方再次尝试,i为尝试次数。
例如,hash1(key) = key mod 5,hash2(key) = key mod 7,当关键码通过hash1映射到的桶非空时,在距离hash1地址hash2(key)的地方再做尝试。
现有{9,8,18,6,5}要按顺序插入表长为5的散列表。
根据第一个散列函数可以确定前两个元素在散列中的地址。
| 0 | 1 | 2 | 3 | 4 |
| 8 | 9 |
到第三个元素18时,hash1(18) = 3,而地址为3的桶已经被占用,转到第二个散列函数,hash2(18) = 4,到桶3距离为4的桶是2,2是一个空桶,探测成功。
| 0 | 1 | 2 | 3 | 4 |
| 18 | 8 | 9 |
伪随机试探:试探间隔可以使用伪随机数发生器,同样可移植性上需要考虑。
查找链:开放定址法构造的散列表中,冲突的元素会形成一个序列,进行查找操作时,将从关键码原本应该在的桶开始,沿这一序列进行查找,这就是查找链。
懒惰删除:查找链使散列表无法进行真正的删除操作,因为一旦删除了一个桶,冲突元素形成的查找序列即查找链就会断开,导致后续查找操作无法进行。
解决办法是设置删除标记,在设计类时加入一个删除标记变量,当一个元素需要被删除,将其赋予特定的值(比如0),这样当查找链扫描到该桶时,将会直接跳过该桶而转到下一个桶单元。而当进行插入操作时,该桶的删除标记将该桶的状态等效为空,如果有符合条件的关键码,直接进行覆盖即可。
设置删除标记的空间开销不过一个变量,非常廉价,而当散列表的规模大到一定程度时,这点开销足可以忽略。
3)再散列
再散列和双散列是完全不同的东西。双散列是开放定址法的一种思路,而再散列是一种扩充散列容量的策略。
扩容:和向量扩容的基本思路相似,用装填因子来衡量散列表中的空间利用率,随着插入的元素越来越多,装填因子变大,到达一定值时,新建一个比原来大的散列表,将原散列中依次插入,形成新的散列表,这就完成了散列的扩容。
扩容的策略:
(1)表满一半进行扩容
(2)当插入失败时扩容
(3)装填因子达到某值时进行扩容
第三种策略最优。
代码实现:
1 HashTable Rehash(HashTable H) 2 { 3 int i, OldSize; 4 Cell *OldSize; 5 OldSize = H->TheCells; 6 OldSize = H->TableSize; 7 H = InitializeTable(2 * OldSize); 8 for (i = 0; i < OldSize; ++i) 9 if (OldCells[i].Info == Legitimate) 10 Insert(OldCells[i].Element, H); 11 free(OldCells); 12 return H; 13 }
4.散列的应用
挖坑待填。
参考资料【1】《数据结构(C++语言版)》 邓俊辉
【2】《数据结构与算法分析——C语言描述》 Mark Allen Weiss


 浙公网安备 33010602011771号
浙公网安备 33010602011771号