数据结构应用 - 二叉树

1.表达式树

描述：表达式树的叶节点为操作数，其他节点为运算符。

对表达式式树采用不同的遍历策略可以分别得到前中后缀三种表达式。

先序遍历：前缀表达式（不常用）

中序遍历：中缀表达式

后序遍历：后缀表达式

构造表达式树：把后缀表达式转化为表达式树（中缀转后缀已经在栈的应用中提到过），本质上还是借助了栈。

类似后缀表达式求值，从头开始逐字符读入表达式，遇到操作数则建立一个单节点树，将其指针压入栈中，当遇到运算符时，将栈顶的两个指针弹出并作为当前运算符的子节点构成一棵二叉树，将该树的指针压入栈中。

读到表达式末尾时，留在栈中的只剩下指向最终的表达式树的指针。

 

2.编码树

编码：将信息转化为二进制码传输的过程就是编码。

解码：将接受到的二进制码恢复为原信息就是解码。

编码表：字符集中的任意字符都能在编码表中找到唯一对应的二进制串。字符集到编码表是单射。

解码歧义：编码可以做到一一对应，解码却未必。比如，规定S->11，M->111，那么现有二进制串“111111”，这个二进制串应该解码为SSS还是MM呢？这就产生了歧义。

产生歧义的根源在于，编码表中的某些编码，是其他编码的前缀。在上例中，S对应的11就是M对应的111的前缀。

前缀无歧义编码（PFC）：既然知道了产生歧义的根源，就可以针对此根源来避免歧义。避免歧义的本质要求就是，保证字符集中的每一个字符所对应的二进制串不是编码表中其他任何二进制串的前缀。

二叉编码树：用二叉树来描述编码方案。我们知道从二叉树的根节点到任一其他节点的通路是唯一的，那么如果，我们使每一个节点之间的通路都表示二进制码0和1（左通路0，右通路1），这样从根节点出发到某节点的通路就变成了一个唯一的二进制串。

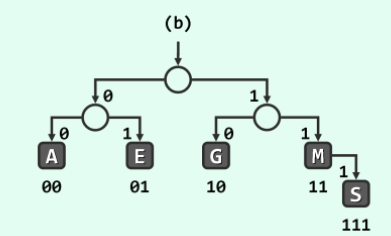
↑一棵普通的二叉编码树，来自《数据结构（C++语言版）》  邓俊辉

PFC编码树：由上图可以清晰地看出，S所对应的二进制码之所以会成为M（所对应的二进制码）的前缀，是因为S是M的子节点。

换而言之，只要字符集中的字符在编码树中存在父子节点的关系，就一定会产生歧义。反过来说，只要在编码树中，字符集中的任一字符都不是字符集中其他某字符的子节点，也就是所有字符都是编码树的叶节点，就一定不会产生歧义。如下图。

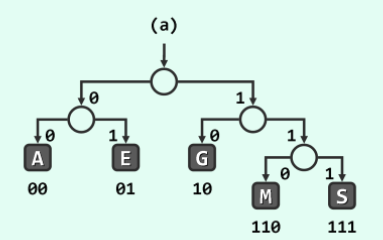
这就是一棵PFC编码树。

PFC编码树的解码：只要根据01子串找到其代表的唯一通路就能找到对应的子节点中的信息。这种解码不必等二进制码完全接收后开始，接收过程中即可开始解码。

 

3.Huffman树

先回顾一下几个关于节点的定义。

节点的权：权值是树或者图中两个结点路径上的值，这个值表明一种代价，如从一个结点到达另外一个结点的路径的长度、所花费的时间、付出的费用等。

Huffman树中的权值可以理解为：权值大表明出现概率大。

节点的带权路径长度：该节点的权值与该节点到根节点的路径的长度的乘积。

树的带权路径长度（WPL）：所有叶节点的带权路径长度之和。

至此可以给出Huffman树的定义：在权为w1,w2,…,wn的n个叶子结点的所有二叉树中，带权路径长度WPL最小的二叉树称为Huffman树或最优二叉树。

Huffman树的构造：（来自百度百科）

假设有n个权值，则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn，则哈夫曼树的构造规则为：

(1) 将w1、w2、…，wn看成是有n 棵树的森林(每棵树仅有一个结点)；

(2) 在森林中选出两个根结点的权值最小的树合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；

(3)从森林中删除选取的两棵树，并将新树加入森林；

(4)重复(2)、(3)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。

Huffman树的一些注意点：原博地址

1、满二叉树不一定是哈夫曼树  

2、哈夫曼树中权越大的叶子离根越近  （很好理解，WPL最小的二叉树）

3、具有相同带权结点的哈夫曼树不惟一

4、哈夫曼树的结点的度数为 0 或 2， 没有度为 1 的结点。

5、包含 n 个叶子结点的哈夫曼树中共有 2n – 1 个结点。

6、包含 n 棵树的森林要经过 n–1 次合并才能形成哈夫曼树，共产生 n–1 个新结点

Huffman编码树：在所有组成节点的权值相同的二叉树中，Huffman树的带权路径长度最短，利用这一性质，可以缩小传输信息时的二进制码的长度。

将字符在字符串中出现的概率（频率）作为节点的权。

构造Huffman编码树：有以下几个要点

（1）求出每种字符在字符串中出现的概率（权）

（2）由于需要不断生成新树删除旧树，借助辅助向量存放

频率统计：

int* statistics ( char* sample_text_file ) { //统计字符出现频率
   int* freq = new int[N_CHAR];  //以下统计需随机访问，故以数组记录各字符出现次数
   memset ( freq, 0, sizeof ( int ) * N_CHAR ); //清零
   FILE* fp = fopen ( sample_text_file, "r" ); //assert: 文件存在且可正确打开
   for ( char ch; 0 < fscanf ( fp, "%c", &ch ); ) //逐个扫描样本文件中的每个字符
      if ( ch >= 0x20 ) freq[ch - 0x20]++; //累计对应的出现次数
   fclose ( fp ); return freq;
}

初始化Huffman森林：

将求得的频率对应到每个节点。

HuffForest* initForest ( int* freq ) { //根据频率统计表，为每个字符创建一棵树
   HuffForest* forest = new HuffForest; //以List实现的Huffman森林
   for ( int i = 0; i < N_CHAR; i++ ) { //为每个字符
      forest->insertAsLast ( new HuffTree ); //生成一棵树，并将字符及其频率
      forest->last()->data->insertAsRoot ( HuffChar ( 0x20 + i, freq[i] ) ); //存入其中
   }
   return forest;
}

构造：

时间复杂度O(n²)

HuffTree* minHChar ( HuffForest* forest ) { //在Huffman森林中找出权重最小的（超）字符
   ListNodePosi ( HuffTree* ) p = forest->first(); //从首节点出发查找
   ListNodePosi ( HuffTree* ) minChar = p; //最小Huffman树所在的节点位置
   int minWeight = p->data->root()->data.weight; //目前的最小权重
   while ( forest->valid ( p = p->succ ) ) //遍历所有节点
      if ( minWeight > p->data->root()->data.weight ) //若当前节点所含树更小，则
         {  minWeight = p->data->root()->data.weight; minChar = p;  } //更新记录
   return forest->remove ( minChar ); //将挑选出的Huffman树从森林中摘除，并返回
}

HuffTree* generateTree ( HuffForest* forest ) { //Huffman编码算法
   while ( 1 < forest->size() ) {
      HuffTree* T1 = minHChar ( forest ); HuffTree* T2 = minHChar ( forest );
      HuffTree* S = new HuffTree(); 15       S->insertAsRoot ( HuffChar ( '^', T1->root()->data.weight + T2->root()->data.weight ) );
      S->attachAsLC ( S->root(), T1 ); S->attachAsRC ( S->root(), T2 );
      forest->insertAsLast ( S ); /*DSA*/ //print(forest);
   } //assert: 循环结束时，森林中唯一（列表首节点中）的那棵树即Huffman编码树
   return forest->first()->data;
}

由Huffman树生成编码表：

static void //通过遍历获取各字符的编码
generateCT ( Bitmap* code, int length, HuffTable* table, BinNodePosi ( HuffChar ) v ) {
   if ( IsLeaf ( *v ) ) //若是叶节点（还有多种方法可以判断）
      {  table->put ( v->data.ch, code->bits2string ( length ) ); return;  }
   if ( HasLChild ( *v ) ) //Left = 0
      { code->clear ( length ); generateCT ( code, length + 1, table, v->lc ); }
   if ( HasRChild ( *v ) ) //Right = 1
      { code->set ( length ); generateCT ( code, length + 1, table, v->rc ); }
}

HuffTable* generateTable ( HuffTree* tree ) { //将各字符编码统一存入以散列表实现的编码表中
   HuffTable* table = new HuffTable; Bitmap* code = new Bitmap;
   generateCT ( code, 0, table, tree->root() ); release ( code ); return table;
};

 

参考资料【1】《数据结构（C++语言版）》  邓俊辉

　　　　【2】《数据结构与算法分析——C语言描述》    Mark Allen Weiss

　　　　【3】《大话数据结构》  程杰