【Coel.学习笔记】【绝唱】自适应辛普森算法

退役了，随便写点东西留给后人得了。

前言

自适应辛普森算法是基于普通辛普森算法给出的一种求近似数值积分的算法。它可以在精度和时间复杂度上进行平衡，从而保证求数值积分的高效性。

前置知识

定积分

~~旧高考的数学课本还简单讲一下定积分的求法，新高考课本只把微积分当做一个研究性学习，太坏了！~~

简单来说，对于一个函数 $f(x)$ 而言， $\int_L^R f(x) \mathrm d x$ 表示直线 $x=L,x=R$ 和 $y=f(x)$ 围成的面积。其中 $x$ 轴上半部分取正值，下半部分取负值。

基本积分公式一则

其他基本积分公式请自行查阅资料。

\int x^{α} d x = \frac{1}{1 + α} x^{1 + α} + C

$\int x^\alpha \mathrm d x=\dfrac{1}{1+\alpha}x^{1+\alpha}+C$

这个公式为不定积分公式，故 $C$ 是一个任意常数。

运用到定积分上的话，根据牛顿-莱布尼茨公式，只要把 $R$ 和 $L$ 分别代入再相减即可。

笔记正文

三点辛普森公式

三点辛普森公式的基本思想是用 $(L,f(L)),(R,f(R)),(mid,f(mid))$ 三点作一个二次函数，用二次函数的积分拟合原本函数的积分。

假设我们求得的二次函数为 $F(x)=ax^2+bx+c$ ，根据基本积分公式，我们可以推导出（注意推导目的是用原函数来表示积分结果）
$\int_L^R F(x)\text d x$
$=\dfrac{a}{3}(R^3-L^3)+\dfrac{b}{2}(R^2-L^2)+c(R-L)$
$=(R-L)[\dfrac{a}{3}(L^2+R^2+LR)+\dfrac{b}{2}(L+R)+c]$ （立方差、平方差公式）
$=\dfrac{R-L}{6}[(aL^2+bL+c)+(aR^2+bR+c)+4(a\dfrac{l+r}{2})^2+4b\dfrac{L+R}{2}+4c]$
$=\dfrac{R-L}{6}[f(L)+f(R)+4F(\dfrac{L+R}{2})]$

这就是所谓的辛普森公式。

其实可以发现，除了基本积分公式以外的推导过程都是初中内容w

自适应辛普森算法

上面都是数学理论分析，下面我们从 OI 角度看看运用。
首先当然是写一个辛普森公式的函数——

int simpson(int l, int r) { //这里做了 #define double int
    // f(x) 为题目要求的函数
    int mid = (l + r) / 2;
    return (r - l) * (f(l) + f(r) + 4 * f(mid)) / 6;
}

然后是自适应的过程。自适应听起来很高大上，但其实就是二分 + 控制精度。

假设我们要求 $[l, r]$ 上的积分，则先用辛普森公式求出这一段用抛物线拟合的积分，再分成两段递归求积分并加和。如果这加和结果和拟合出来的结果相差很小，就可以直接跳出递归。

一般来说我们还要控制递归层数，经验上 $12$ 层递归比较好。

int adaptiveSimpson(int l, int r, int eps, int res, int dep) {
    double mid = (l + r) / 2, L = simpson(l, mid), R = simpson(mid, r);
    if (abs(L + R - res) <= 15 * eps && dep < 0)
        return L + R + (L + R - res) / 15;
    return adaptiveSimpson(l, mid, eps / 2, L, dep - 1) +
        adaptiveSimpson(mid, r, eps / 2, R, dep - 1);
}

int calc(int l, int r, int eps) {
    return adaptiveSimpson(l, r, eps, simpson(l, r), 12);
}

例题简析

接下来看几道例题。

【模板】自适应辛普森法 1

洛谷传送门
求解

\int_{L}^{R} \frac{c x + d}{a x + b} d x

$\displaystyle{\int_L^R\frac{cx+d}{ax+b}\mathrm{d}x}$

保留 $6$ 位小数。

解析：非常模板，直接套就行，不多说。

#include <iostream>
#include <cmath>
#include <iomanip>

#define int long double

using namespace std;

int a, b, c, d, l, r;

int f(int x) {
	return (c * x + d) / (a * x + b);
}

int simpson(int l, int r) {
	int mid = (l + r) / 2;
	return (r - l) * (f(l) + f(r) + 4 * f(mid)) / 6;
}

int adaptiveSimpson(int l, int r, int eps, int res, int dep) {
	double mid = (l + r) / 2, L = simpson(l, mid), R = simpson(mid, r);
	if (abs(L + R - res) <= 15 * eps && dep < 0)
		return L + R + (L + R - res) / 15;
	return adaptiveSimpson(l, mid, eps / 2, L, dep - 1) +
		adaptiveSimpson(mid, r, eps / 2, R, dep - 1);
}

int calc(int l, int r, int eps) {
	return adaptiveSimpson(l, r, eps, simpson(l, r), 12);
}

signed main() {
	cin >> a >> b >> c >> d >> l >> r;
	cout << fixed << setprecision(6) << calc(l, r, 1e-6);
	return 0;
}

【模板】自适应辛普森法 2

洛谷传送门
求解

\int_{0}^{\infty} x^{\frac{a}{x} - x} d x

$\displaystyle{\int_0^\infty x^{\frac{a}{x}-x}\mathrm{d}x}$

若发散（即极限不存在）则输出 $\text{orz}$ ，否则保留 $5$ 位小数。

解析：这是个上限正无穷的积分，也就是一个广义积分（即反常积分）。显然直接用辛普森法是不可求的~~（不可能直接在代码写个 $R=\infty$ 吧）~~，但我们可以用计算器或者 Geogebra 看看图像：

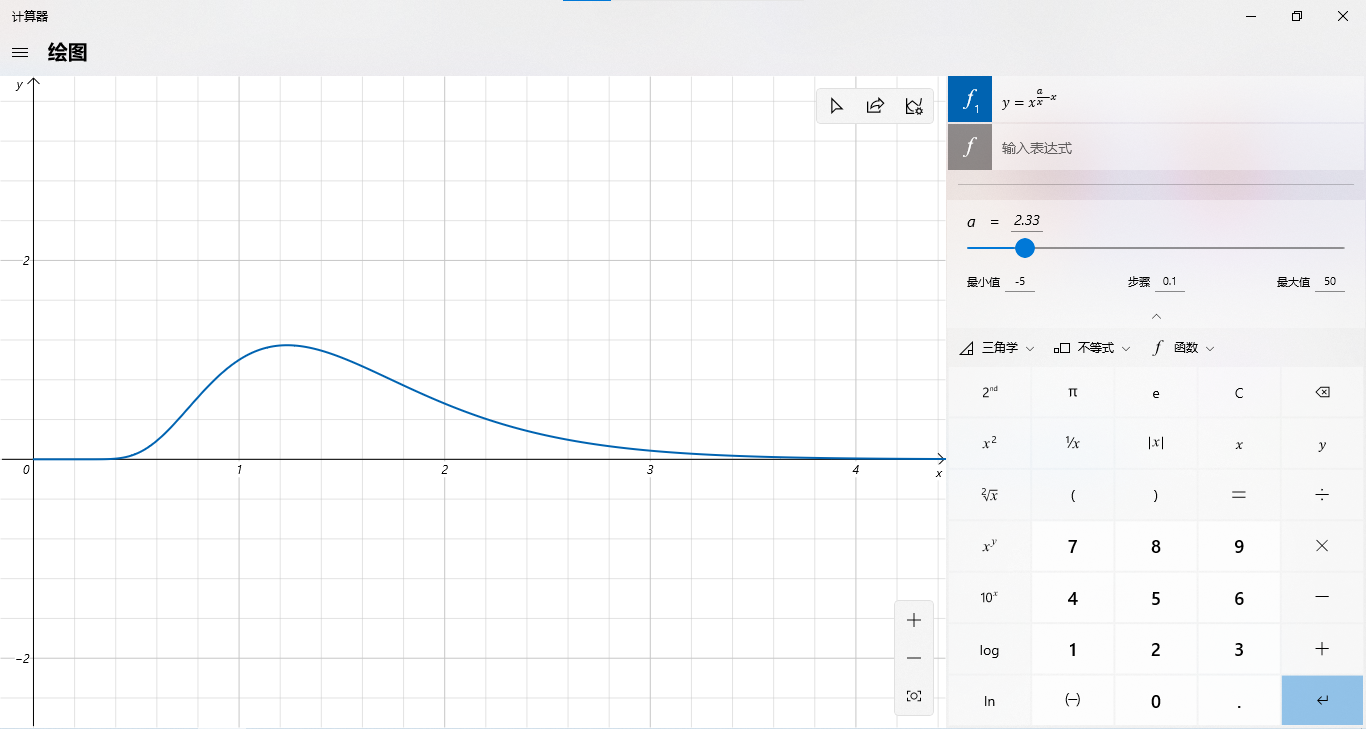
不难发现函数的后半部分单调递减且趋近于 $0$ ，考虑到精度要求，我们只要取一小段即可。当 $a=50$ 时 $x=8$ 就已经非常贴近 $x$ 轴了，保险起见我们可以开大一点，这里设了 $20$ 。

那么什么时候发散呢？同样看看图像：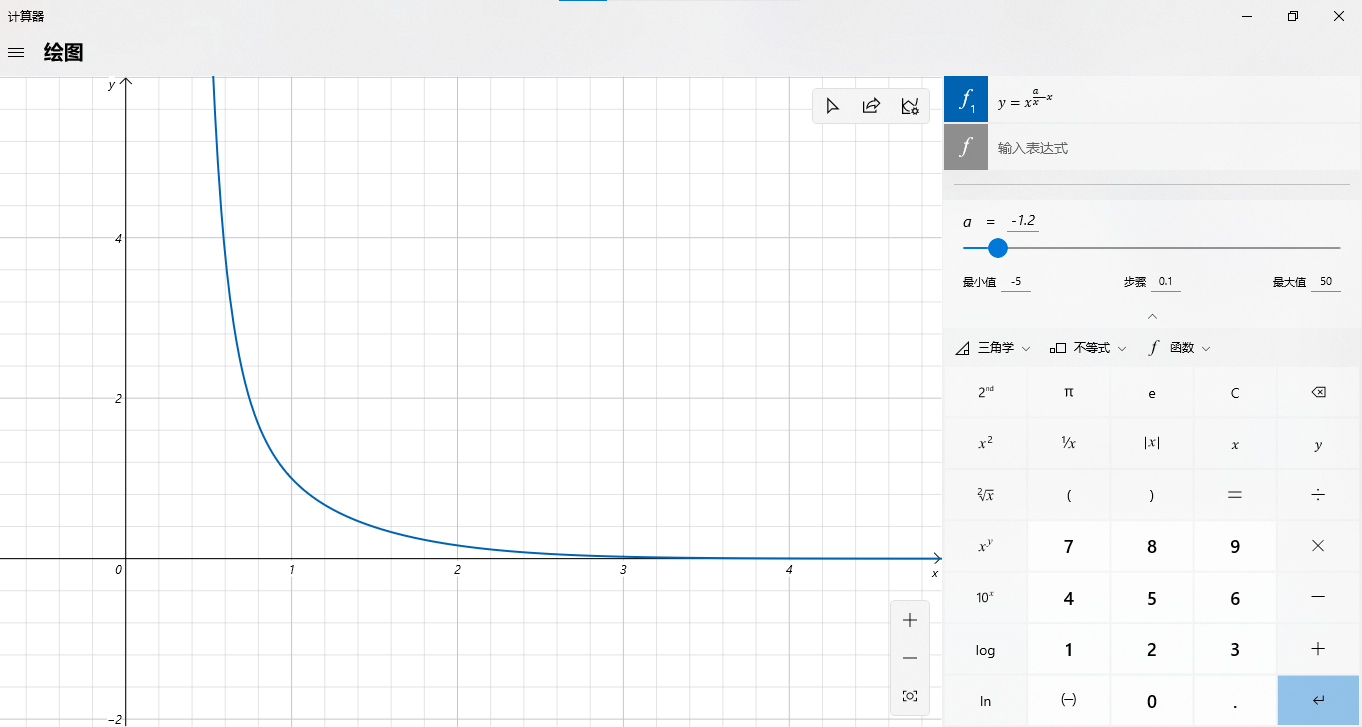
显然 $a<0$ 的时候左边无限趋近于正无穷，是发散的。当然严格证明也不难，请读者自行思考。

#include <iostream>
#include <cmath>
#include <iomanip>

#define int long double

using namespace std;

const int eps = 1e-9;
//保险起见 eps 开小一点
int a;

int f(int x) {
	return pow(x, (a / x) - x);
}

int simpson(int l, int r) {
	int mid = (l + r) / 2;
	return (r - l) * (f(l) + f(r) + 4 * f(mid)) / 6;
}

int adaptiveSimpson(int l, int r, int eps, int res, int dep) {
	double mid = (l + r) / 2, L = simpson(l, mid), R = simpson(mid, r);
	if (abs(L + R - res) <= 15 * eps && dep < 0)
		return L + R + (L + R - res) / 15;
	return adaptiveSimpson(l, mid, eps / 2, L, dep - 1) +
		adaptiveSimpson(mid, r, eps / 2, R, dep - 1);
}

int calc(int l, int r, int eps) {
	return adaptiveSimpson(l, r, eps, simpson(l, r), 12);
}

signed main() {
	cin >> a;
	if (a < 0) cout << "orz";
	else cout << fixed << setprecision(5) << calc(eps, 15, eps);
	//这里下限设置为 eps，防止 a = 0 时计算出错
	return 0;
}

和辛普森算法的题目非常少，而且基本上都是用来求面积的“几何”题。这里对于几何题不作介绍，而是给出一个更特别一点的题目。

「SDOI2017」龙与地下城

洛谷传送门
有 $Y$ 个 $X$ 面骰子，每个骰子的点值均在 $0\sim X-1$ 之间，且每个面出现的概率均为 $\dfrac{1}{X}$ 。对于每个给定的 $A,B$ ，求出点数之和在 $[A,B]$ 的概率。
原题中提示：骰子点值之和的期望为 $\dfrac{X-1}{2}$ ，方差为 $\dfrac{X^2-1}{12}$ 。
解析：对于小数据，我们考虑使用动态规划。计 $f_{i,j}$ 表示对于前 $i$ 个骰子，点数之和为 $j$ 的概率，可以写出状态转移方程

f_{i, j} = \sum_{0 \leq k \leq min (j, X - 1)} f (i - 1, j - k) \frac{1}{X}

$f_{i,j}=\sum_{0\leq k \leq\min (j, X - 1)} f(i-1,j-k)\dfrac{1}{X}$

而转移过程可以转化为求多项式快速幂的各项系数和，所以可以用快速傅里叶变换优化转移，此时时间复杂度为 $O(XY\log XY)$ ，可以通过 $XY\leq 4\times 10^5$ 的数据，但对于更大（即编号 $13\sim 20$ 的部分）的数据就没办法了。

考察一下二项分布的性质。在数学课本上应该有所介绍：当随机变量取值范围足够大时，二项分布、超几何分布、正态分布可以互相近似。事实上，这是中心极限定理的一个小应用，考虑到篇幅限制，这里不作展开介绍。

知道了这么一个性质，再加上题目的提示已经给出了点数之和的期望与方差，我们就可以直接对正态曲线做积分来求解了。

综合以上办法，我们可以对 $XY$ 较小的数据用快速傅里叶变换，对大数据使用自适应辛普森算法。

#include <iostream>
#include <cmath>
#include <iomanip>
#include <cstring>

using namespace std;

const int maxn = 6e5 + 10, Boundery = 4e5 + 10;
const double pi = 3.1415926535, Gauss = 1 / sqrt(2 * pi), eps = 1e-7;

int T, x, y, tot;

// ----- Solve with FFT-----

struct complex {//这里都是 FFT 的模板，可以在之前的文章中找到
	double x, y;
	complex operator+(const complex &t) const {
		return {x + t.x, y + t.y};
	}
	complex operator-(const complex &t) const {
		return {x - t.x, y - t.y};
	}
	complex operator*(const complex &t) const {
		return {x * t.x - y * t.y, x * t.y + y * t.x};
	}
} res[maxn];

int rev[maxn], bit;

void remake() {
	for (int i = 0; i < tot; i++)
		res[i].x = res[i].y = 0;
	memset(rev, 0, sizeof(rev));
}

void init_bit() {
	bit = 0;
	while ((1 << bit) <= tot) bit++;
	tot = 1 << bit;
	for (int i = 0; i < tot; i++)
		rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
}

complex qpow(complex a, int y) {
	complex x = {1, 0};
	while (y) {
		if (y % 2 == 1) x = x * a;
		a = a * a;
		y >>= 1;
	}
	return x;
}

void fft(complex a[], int inv) {
	for (int i = 0; i < tot; i++)
		if (i < rev[i]) swap(a[i], a[rev[i]]);
	for (int mid = 1; mid < tot; mid <<= 1) {
		auto w1 = complex({cos(pi / mid), inv * sin(pi / mid)});
		for (int i = 0; i < tot; i += mid * 2) {
			auto wk = complex({1, 0});
			for (int j = 0; j < mid; j++, wk = wk * w1) {
				auto x = a[i + j], y = wk * a[i + j + mid];
				a[i + j] = x + y, a[i + j + mid] = x - y;
			}
		}
	}
}

// -----Solve with adaptiveSimpson-----

double f(double x) { //标准正态分布的公式
	return Gauss * exp(-x * x / 2.0);
}

double simpson(double l, double r) {
	double mid = (l + r) / 2;
	return (r - l) * (f(l) + f(r) + 4 * f(mid)) / 6;
}

double adaptiveSimpson(double l, double r, double eps, double res, double dep) {
	double mid = (l + r) / 2, L = simpson(l, mid), R = simpson(mid, r);
	if (abs(L + R - res) <= 15 * eps && dep < 0)
		return L + R + (L + R - res) / 15;
	return adaptiveSimpson(l, mid, eps / 2, L, dep - 1) +
	adaptiveSimpson(mid, r, eps / 2, R, dep - 1);
}

double calc(double l, double r, double eps) {
	return adaptiveSimpson(l, r, eps, simpson(l, r), 12);
}

int main(void) {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cin >> T;
	while (T--) {
		double a, b;
		cin >> x >> y;
		tot = x * y;
		if (tot > Boundery) {
			double mu = (x * 1.0 - 1) / 2, sigma = (x * x * 1.0 - 1) / 12;
			for (int i = 1; i <= 10; i++) {
				cin >> a >> b;
				a = (a - y * mu) / sqrt(y * sigma), b = (b - y * mu) / sqrt(y * sigma); //把一般正态分布转换为标准正态分布
				cout << fixed << setprecision(6) << calc(a, b, eps) << '\n'; //对 [A,B] 进行积分
			}
			tot = 0;
		} else {
			init_bit();
			for (int i = 0; i < x; i++) res[i].x = 1 / (x * 1.0);
			fft(res, 1);
			for (int i = 0; i < tot; i++) res[i] = qpow(res[i], y);
			fft(res, -1);//多项式系数快速幂
			for (int i = 0; i < tot; i++) res[i].x /= tot, res[i].y /= tot;
			for (int i = 1; i <= 10; i++) {
				int a, b;
				cin >> a >> b;
				double ans = 0;
				for (int j = a; j <= b; j++) ans += res[j].x; //求和即可得到答案
				cout << fixed << setprecision(6) << ans << '\n';
			}
		}
		remake();
	}
	return 0;
}

本文作者：Coel's Blog

本文链接：https://www.cnblogs.com/Coel-Flannette/p/17127706.html

posted @ 2023-02-16 17:52 秋泉こあい阅读(73) 评论(1) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

2025年3月

日

一

二

三

四

五

六

Coel's Blog

【Coel.学习笔记】【绝唱】自适应辛普森算法

前言

前置知识

定积分

基本积分公式一则

笔记正文

三点辛普森公式

自适应辛普森算法

例题简析

【模板】自适应辛普森法 1

【模板】自适应辛普森法 2

「SDOI2017」龙与地下城

搜索

常用链接

随笔分类

随笔档案

阅读排行榜

评论排行榜

推荐排行榜

最新评论