【Coel.学习笔记】树链剖分

前言

树链剖分是一种思想，通过给树中每一个点重新编号，使得树中任意一条路径都可以转化为 \(O(\log n)\) 段连续区间，从而利用线段树或树状数组解决某些树上路径问题。树链剖分也是连切动态树的重要前置知识。

树链剖分中有一些特别的概念与性质。

概念

轻重儿子：一个非叶子节点的子树可以分为两个，子树更大的节点为重儿子，反之为轻儿子。有多个相同子树大小的话，任取其中一个为重儿子，其余均为轻儿子。
轻重边：重儿子与父节点的边为重边，其余为轻边。
重链：由重边构成的极大路径。单独的点本身也可以构成一个重链。
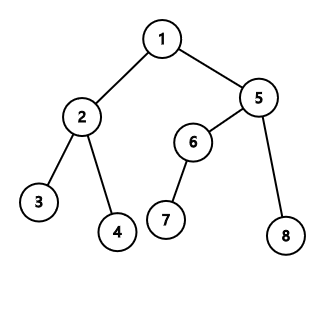
如下图，重儿子为节点 \(3,5,6,7\)，重边为 \((2,3),(1,5),(5,6),(6,7)\)，重链为 \((1,5,6,7),(2,3),(4),(8)\)。

性质

树中任意一条路径都可以拆分成 \(O(\log n)\) 条重链。 在 dfs 时，我们优先遍历重儿子，这样可以保证重链上每个点的编号连续，从而拆分出 \(O(\log n)\) 个连续区间。

例题

【模板】轻重链剖分/树链剖分

洛谷传送门
已知一棵包含 \(N\) 个结点的树（连通且无环），每个节点上包含一个数值，需要支持以下操作：

• 1 x y z，表示将树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值都加上 \(z\)。
• 2 x y，表示求树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值之和。
• 3 x z，表示将以 \(x\) 为根节点的子树内所有节点值都加上 \(z\)。
• 4 x 表示求以 \(x\) 为根节点的子树内所有节点值之和。

解析：对于操作一，我们通过树链剖分分出区间后直接利用线段树的区间加；
对于操作二，通过轻重链剖分分解区间，然后区间求和；
对于操作三，我们在搜索时做到了连续编号，可以直接线段树修改；
对于操作四，同上进行区间求和即可。

可以发现，进行树链剖分后，所有操作都可以转化为区间的修改与查询操作。因此，我们操作的关键就在树链剖分的实现上。采用两遍 dfs，第一次求出所有的重儿子、子树大小和父节点，第二次按照重儿子优先的方式求 dfs 序。

预处理树链剖分的时间复杂度为 \(O(n)\)。单次操作时，对于序列操作，每次都要利用重链分出的区间进行查询和修改，再乘上线段树的时间复杂度，总共为 \(O(\log ^2 n)\)；对于子树操作，每次只要在对应的区间上做线段树查询修改即可，时间复杂度为 \(O(\log n)\)。总时间复杂度为 \(O(n\log^2n)\)。

代码如下：

#include <cstring>
#include <iostream>

using namespace std;

const int maxn = 2e5 + 10;

typedef long long ll;

int n, m, r, p;
int head[maxn], nxt[maxn], to[maxn], w[maxn], cnt;
int id[maxn], nw[maxn], idx;
int dep[maxn], sz[maxn], top[maxn], fa[maxn], son[maxn];
//dep:节点深度 sz:子树大小 top:节点所在重链的最高点 fa:父节点 son:重儿子

struct Segment_Tree {
    int l, r;
    ll tag, sum;
} T[maxn << 2];

void add(int u, int v) { nxt[cnt] = head[u], to[cnt] = v, head[u] = cnt++; }

void dfs1(int u, int f, int d) {
    dep[u] = d, fa[u] = f, sz[u] = 1;
    for (int i = head[u]; ~i; i = nxt[i]) {
        int v = to[i];
        if (v == f) continue;
        dfs1(v, u, d + 1);
        sz[u] += sz[v];
        if (sz[son[u]] < sz[v]) son[u] = v;//更新重儿子
    }
}

void dfs2(int u, int t) {//t 表示当前的 top
    id[u] = ++idx, nw[idx] = w[u], top[u] = t;
    if (!son[u]) return;
    dfs2(son[u], t);//优先遍历重儿子
    for (int i = head[u]; ~i; i = nxt[i]) {
        int v = to[i];
        if (v == fa[u] || v == son[u]) continue;
        dfs2(v, v);//由于重儿子遍历过了，所以另起一段链
    }
}

void pushup(int u) { T[u].sum = (T[u << 1].sum + T[u << 1 | 1].sum) % p; }

void pushdown(int u) {
    auto &root = T[u], &left = T[u << 1], &right = T[u << 1 | 1];
    if (root.tag) {
        (left.tag += root.tag) %= p;
        (left.sum += root.tag * (left.r - left.l + 1) % p) %= p;
        (right.tag += root.tag) %= p;
        (right.sum += root.tag * (right.r - right.l + 1) % p) %= p;
        root.tag = 0;
    }
}

void build(int u, int l, int r) {
    T[u] = {l, r, 0, nw[r]};
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
    pushup(u);
}

void modify(int u, int l, int r, int k) {
    if (l <= T[u].l && r >= T[u].r) {
        (T[u].tag += k) %= p;
        (T[u].sum += k * (T[u].r - T[u].l + 1) % p) %= p;
        return;
    }
    pushdown(u);
    int mid = (T[u].l + T[u].r) >> 1;
    if (l <= mid) modify(u << 1, l, r, k);
    if (r > mid) modify(u << 1 | 1, l, r, k);
    pushup(u);
}

ll query(int u, int l, int r) {
    if (l <= T[u].l && r >= T[u].r) return T[u].sum;
    pushdown(u);
    int mid = (T[u].l + T[u].r) >> 1;
    ll res = 0;
    if (l <= mid) (res += query(u << 1, l, r)) %= p;
    if (r > mid) (res += query(u << 1 | 1, l, r)) %= p;
    return res;
}

void modify_path(int u, int v, int k) {
    while (top[u] != top[v]) {//类似倍增，每次跳一条链
        if (dep[top[u]] < dep[top[v]]) swap(u, v);
        modify(1, id[top[u]], id[u], k);
        u = fa[top[u]];
    }
    if (dep[u] < dep[v]) swap(u, v);
    modify(1, id[v], id[u], k);
}

ll query_path(int u, int v) {//查询和修改对偶
    ll res = 0;
    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) swap(u, v);
        (res += query(1, id[top[u]], id[u])) %= p;
        u = fa[top[u]];
    }
    if (dep[u] < dep[v]) swap(u, v);
    (res += query(1, id[v], id[u])) %= p;
    return res;
}

int main(void) {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> n >> m >> r >> p;
    for (int i = 1; i <= n; i++) cin >> w[i];
    memset(head, -1, sizeof(head));
    for (int i = 1; i <= n - 1; i++) {
        int u, v;
        cin >> u >> v;
        add(u, v), add(v, u);
    }
    dfs1(r, -1, 1);
    dfs2(r, r);
    build(1, 1, n);
    while (m--) {
        int op, u, v, k;
        cin >> op >> u;
        if (op == 1) {
            cin >> v >> k;
            modify_path(u, v, k);
        } else if (op == 2) {
            cin >> v;
            cout << query_path(u, v) << '\n';
        } else if (op == 3) {
            cin >> k;
            modify(1, id[u], id[u] + sz[u] - 1, k);
        } else
            cout << query(1, id[u], id[u] + sz[u] - 1) << '\n';
    }
    return 0;
}

[NOI2015] 软件包管理器

洛谷传送门
给定若干个节点和这些节点对应的父节点，在一棵初始为空的树上进行操作。每次操作会插入或删除一个节点，求出每次操作后会使多少节点的状态变化。操作保证树上不出现环，且 \(0\) 号节点必定为根节点。

解析：我们可以先按照题目所给的对应关系建树，用 \(1\) 表示在树上，\(0\) 表示不在树上。

对于插入操作，相当于求该节点到父节点中 \(0\) 的个数，然后全部赋值为 \(1\)；求 \(0\) 个数就相当于用这个点的深度减去路径和，全部赋值直接用线段树。

对于删除操作，相当于求该节点的子树中 \(1\) 的个数，然后全部赋值为 \(0\)；直接求出子树权值和再全部赋值即可。

这个想法很显然，但实际上还可以优化：因为我们本质上求的就是修改之后与修改之前的差值，而且除了修改的部分，其他部分都是不变的，所以这个操作可以改写成赋值前后 T[1].sum 的差，这样写可以减少一半的常数，而且不需要实现查询操作。

很显然，直接用树链剖分的模板就可以实现所有操作，把线段树的区间加改成区间赋值即可。原题以 \(0\) 为节点，求树链剖分的时候有一点麻烦，我们可以把所有编号加上 \(1\)。

#include <cstring>
#include <iostream>

using namespace std;

const int maxn = 2e5 + 10;

typedef long long ll;

int n, m;
int head[maxn], nxt[maxn], to[maxn], w[maxn], cnt;
int id[maxn], idx;
int dep[maxn], sz[maxn], top[maxn], fa[maxn], son[maxn];

struct Segment_Tree {
    int l, r;
    int tag, sum;
} T[maxn << 2];

void add(int u, int v) { nxt[cnt] = head[u], to[cnt] = v, head[u] = cnt++; }

void dfs1(int u, int d) {
    dep[u] = d, sz[u] = 1;
    for (int i = head[u]; ~i; i = nxt[i]) {
        int v = to[i];
        dfs1(v, d + 1);
        sz[u] += sz[v];
        if (sz[son[u]] < sz[v]) son[u] = v;
    }
}

void dfs2(int u, int t) {
    id[u] = ++idx, top[u] = t;
    if (!son[u]) return;
    dfs2(son[u], t);
    for (int i = head[u]; ~i; i = nxt[i]) {
        int v = to[i];
        if (v == fa[u] || v == son[u]) continue;
        dfs2(v, v);
    }
}

void pushup(int u) { T[u].sum = T[u << 1].sum + T[u << 1 | 1].sum; }

void pushdown(int u) {
    auto &root = T[u], &left = T[u << 1], &right = T[u << 1 | 1];
    if (root.tag != -1) {
        left.sum = root.tag * (left.r - left.l + 1);
        right.sum = root.tag * (right.r - right.l + 1);
        left.tag = right.tag = root.tag;
        root.tag = -1;
    }
}

void build(int u, int l, int r) {
    T[u] = {l, r, -1, 0};  //没有标记要写成 -1，否则会和没安装混淆
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}

void modify(int u, int l, int r, int k) {
    if (l <= T[u].l && r >= T[u].r) {
        T[u].tag = k;
        T[u].sum = k * (T[u].r - T[u].l + 1);
        return;
    }
    pushdown(u);
    int mid = (T[u].l + T[u].r) >> 1;
    if (l <= mid) modify(u << 1, l, r, k);
    if (r > mid) modify(u << 1 | 1, l, r, k);
    pushup(u);
}

void modify_path(int u, int v, int k) {
    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) swap(u, v);
        modify(1, id[top[u]], id[u], k);
        u = fa[top[u]];
    }
    if (dep[u] < dep[v]) swap(u, v);
    modify(1, id[v], id[u], k);
}

void modify_tree(int u, int k) { modify(1, id[u], id[u] + sz[u] - 1, k); }

int main(void) {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> n;
    memset(head, -1, sizeof(head));
    for (int i = 2; i <= n; i++) {
        int u;
        cin >> u;
        add(++u, i);
        fa[i] = u; //fa 已经给出，所以没必要建双向边
    }
    dfs1(1, 1);
    dfs2(1, 1);
    build(1, 1, n);
    cin >> m;
    while (m--) {
        int x, t = T[1].sum;
        char op[30];
        cin >> op >> x;
        x++;
        if (!strcmp(op, "install")) {
            modify_path(1, x, 1);
            cout << T[1].sum - t << '\n';
        } else {
            modify_tree(x, 0);
            cout << t - T[1].sum << '\n';
        }
    }
    return 0;
}