【Coel.学习笔记】分块入门

引入

分块是一种暴力数据结构（类似珂朵莉树，但时间复杂度有所保证），尽管不像线段树和树状数组能够在对数时间复杂度完成操作，但能够做到许多线段树、树状数组做不到的操作。

分块

我们从一道简单的区间加、区间求和看一看分块的基本原理。

【模板】线段树

洛谷传送门
已知一个数列，你需要进行下面两种操作：

• 将某区间每一个数加上 $c$
• 求出某区间每一个数的和。

数列长度和操作数 $n,m\leq10^5$。

---

解析：既然叫做“分块”，自然就要把数列分成若干个“块”。记每个块的长度为 $s$。最后一个块可能长度不够 $s$，但是不会影响接下来的操作。显然，这时块的个数是 $O(\dfrac{n}{s})$。

每个块需要维护一些信息。对于这道题，我们需要维护两个信息：一是懒惰标记，记录本段的加法操作；二是区间和，记录本段的加和（包括懒标记记录的操作）。

对于区间修改操作，显然会遇到两种不同的块:中间完整包含的块，和左右两边不完整包含的块。对于完整块而言，直接暴力修改懒惰标记和区间和即可；对于不完整的块而言，枚举被包含的所有数，并对数列本身做修改，区间加上和。时间复杂度为 $O(\dfrac{n}{s}+s)$。

对于查询操作，同样要对两种块分别处理。完整块累加每个块的区间和，不完整的块暴力求和，时间复杂度同样为 $O(\dfrac{n}{s}+s)$。

由高中数学必修一中学到的均值不等式可以知道，当 $\dfrac{n}{s}=s=\sqrt n$ 时，$\dfrac{n}{s}+s$ 有最小值 $2\sqrt n$。因此我们让块的长度为 $\sqrt n$，就可以得到分块的最优时间复杂度 $O(\sqrt n)$。

可以发现，分块的操作十分暴力，但也使得它理解更容易（相对树状数组）、代码长度更短（相对线段树），并且能够解决更多问题（Ynoi 系列一大堆分块题）。缺点也很显然，时间复杂度劣于线段树、树状数组的 $O(\log n)$。

具体实现时，我们要记录下每个数字对应的块，方便进行操作。一种常见的方法是用 $(i-1)\div s$ 表示第 $i$ 个数对应的块。

代码如下（不开 O2 优化也能过，但对于分块来说 O2 优化的效果非常显著）：

#include <cmath>
#include <iostream>

#define int long long
#define get(x) (x - 1) / len

using namespace std;

const int maxn = 1e5 + 10;

int n, m, len;
int add[maxn], sum[maxn], a[maxn];

void modify(int l, int r, int c) {
    if (get(l) == get(r)) //全部在块内，直接算
        for (int i = l; i <= r; i++) a[i] += c, sum[get(i)] += c;
    else {
        int i = l, j = r;
        while (get(i) == get(l)) a[i] += c, sum[get(i)] += c, i++;
        while (get(j) == get(r)) a[j] += c, sum[get(j)] += c, j--;
        for (int k = get(i); k <= get(j); k++) sum[k] += c * len, add[k] += c;
        //分别处理左边、右边和中间的块
    }
}

int query(int l, int r) { //查询和修改是一样的
    int res = 0;
    if (get(l) == get(r))
        for (int i = l; i <= r; i++) res += a[i] + add[get(i)];
    else {
        int i = l, j = r;
        while (get(i) == get(l)) res += a[i] + add[get(i)], i++;
        while (get(j) == get(r)) res += a[j] + add[get(j)], j--;
        for (int k = get(i); k <= get(j); k++) res += sum[k];
    }
    return res;
}

signed main(void) {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> n >> m;
    len = sqrt(n);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        sum[get(i)] += a[i];
    }
    while (m--) {
        int op, l, r, c;
        cin >> op >> l >> r;
        if (op == 1) {
            cin >> c;
            modify(l, r, c);
        } else
            cout << query(l, r) << '\n';
    }
    return 0;
}

块状链表

块状链表是分块思想的一个具体体现，可以实现插入操作。
这里先介绍原理再讲例题，因为例题实在太复杂了

用一张 OI-Wiki 的图片直观感受一下块状链表：

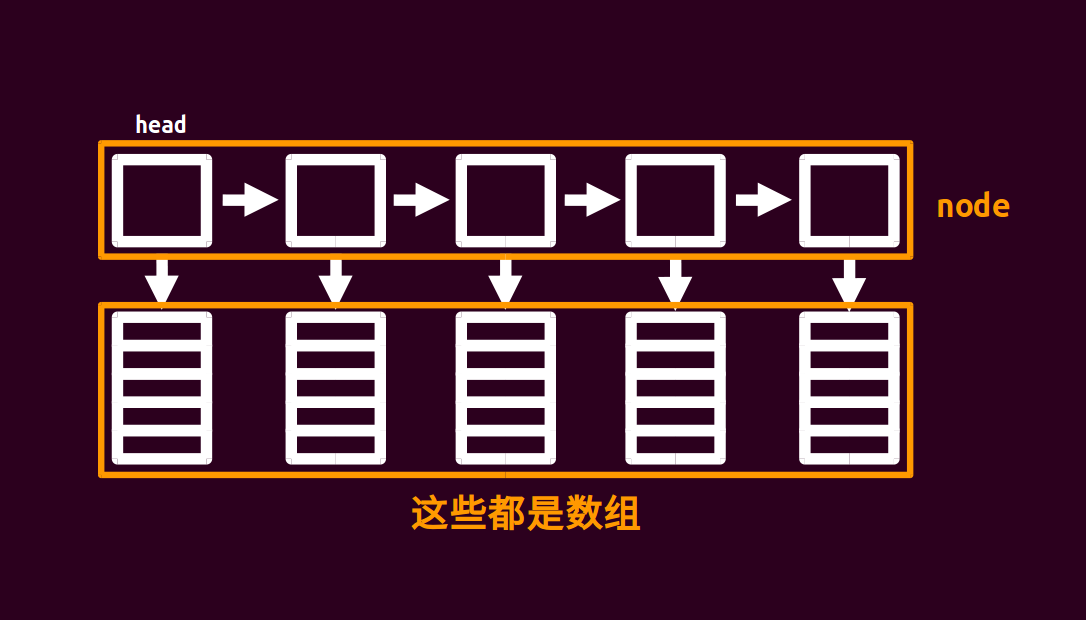
显然块状链表也是一个链表，每个节点对应一个数组。这样就可以实现高效插入。具体地，我们要把待插入位置两边分裂开，再建立一个序列。

如果要删除呢？分三步走：删除开头节点后半部分，删除中间的完整部分，删除结尾节点的前半部分。

要想维护一个块状链表，对于每一块都要维护几个信息：对应的字符串，存放的字串长度，左右相连的值。

现在看看这道题吧……

[NOI2003] 文本编辑器

建立一个文本编辑器，实现以下操作：

操作名称	输入文件中的格式	功能
$\text{Move}(k)$	Move k	将光标移动到第 $k$ 个字符之后，如果 $k=0$，将光标移到文本开头
$\text{Insert}(n,s)$	Insert n s	在光标处插入长度为 $n$ 的字符串 $s$，光标位置不变$n\geq1$
$\text{Delete}(n)$	Delete n	删除光标后的 $n$ 个字符，光标位置不变，$n \geq 1$
$\text{Get}(n)$	Get n	输出光标后的 $n$ 个字符，光标位置不变，$n \geq 1$
$\text{Prev}()$	Prev	光标前移一个字符
$\text{Next}()$	Next	光标后移一个字符

解析：这题可以用 Splay 或者 FHQ-Treap 解决，但也可以用块状链表实现。

对于移动光标操作，从第一个块开始找 $k$ 个字符就是对应的位置。顺带一提，这时光标要保存两个信息：所在的块和块内的位置。
插入和删除上面已经提到过了，这里不再赘述。
输出操作和插入删除一样要断开，不过不需要实际插入删除东西就是了。
移动光标需要特判光标在块边上的情况，除了这点也没什么可以注意的。
移动、插入、删除和输出的操作复杂度均为 $O(\sqrt n)$，移动光标的操作复杂度为 $O(1)$。为了保证复杂度的正确性，我们还得在每次操作后把散块合并起来直到长度保持到 $O(\sqrt n)$。

和维护数列那题一样，这里也可以用内存回收。
说起来很简单，但细节相当多，调试起来极其麻烦。具体看代码吧——
（其实理解起来还是相当容易的，就是比较费 debug 和手）

#include <cctype>
#include <cstdio>
#include <cstring>
#include <iostream>

using namespace std;

const int maxn = 2e3 + 10, mlen = 2e6 + 10;
/*这里的 maxn 其实是取了根号下最大长度*/

int n;

int x, y;  //光标所在分块和所在分块的具体下标

struct node {
    char s[maxn + 1];
    int cnt, l, r;  //字串长度，链表前驱，链表后继
} p[maxn];

char str[mlen];

int q[maxn], idx;  //内存回收

inline int read() {
    int x = 0, f = 1;
    char ch = getchar();
    while (!isdigit(ch)) {
        if (ch == '-') f = -1;
        ch = getchar();
    }
    while (isdigit(ch)) x = x * 10 + ch - '0', ch = getchar();
    return x * f;
}

inline bool check(char x) { return x >= 32 && x <= 126; }

/*以下为维护链表的操作*/

void add(int x, int u) {  //在 x 结点的后方加上 u 结点
    /*这里其实就是一个前驱后继关系变动的问题，可以自己手模一下*/
    p[u].r = p[x].r, p[p[u].r].l = u;
    p[x].r = u, p[u].l = x;
}

void del(int u) {  //删除 u 结点
    p[p[u].l].r = p[u].r;
    p[p[u].r].l = p[u].l;
    p[u].l = p[u].r = p[u].cnt = 0;
    q[++idx] = u;  //内存回收
}

void merge() {  //合并散块，保证时间复杂度正确
    for (int i = p[0].r; i; i = p[i].r)
        while (p[i].r && p[i].cnt + p[p[i].r].cnt < maxn) {
            int r = p[i].r;
            for (int j = p[i].cnt, k = 0; k < p[r].cnt; j++, k++)
                p[i].s[j] = p[r].s[k];
            if (x == r) x = i, y += p[i].cnt;
            p[i].cnt += p[r].cnt;
            del(r);
        }
}

/*以下为具体操作*/

void move(int k) {
    x = p[0].r;
    while (k > p[x].cnt) k -= p[x].cnt, x = p[x].r;  //一步步移动所在块
    y = k - 1;                                       //块内具体位置
}

void insert(int k) {
    if (y < p[x].cnt - 1) {  //不在块的边界，分裂新结点
        int u = q[idx--];
        for (int i = y + 1; i < p[x].cnt; i++) p[u].s[p[u].cnt++] = p[x].s[i];
        p[x].cnt = y + 1;
        add(x, u);
    }
    int cur = x, pos = 0;
    while (pos < k) {
        int u = q[idx--];
        while (p[u].cnt < maxn && pos < k) p[u].s[p[u].cnt++] = str[pos++];
        /*不断加直到满块或加完*/
        add(cur, u);
        cur = u;
    }
}

void remove(int k) {
    if (p[x].cnt - 1 - y >= k) {  //若删完不到达块的边界，直接把后一部分移动到前面
        for (int i = y + k + 1, j = y + 1; i < p[x].cnt; i++, j++)
            p[x].s[j] = p[x].s[i];
        p[x].cnt -= k;  //下标后退
    } else {
        k -= p[x].cnt - y - 1;
        p[x].cnt = y + 1;
        while (p[x].r && k >= p[p[x].r].cnt) {  //删散块
            int u = p[x].r;
            k -= p[u].cnt;
            del(u);
        }
        int u = p[x].r;
        for (int i = 0, j = k; j < p[u].cnt; i++, j++)  //删整块的小部分
            p[u].s[i] = p[u].s[j];
        p[u].cnt -= k;
    }
}

void get(int k) {
    if (p[x].cnt - 1 - y >= k)  //输出内容全部在块内
        for (int i = 0, j = y + 1; i < k; i++, j++) putchar(p[x].s[j]);
    else {
        k -= p[x].cnt - y - 1;
        for (int i = y + 1; i < p[x].cnt; i++) putchar(p[x].s[i]);
        int cur = x;
        while (p[cur].r && k >= p[p[cur].r].cnt) {  //输出散块
            int u = p[cur].r;
            for (int i = 0; i < p[u].cnt; i++) putchar(p[u].s[i]);
            k -= p[u].cnt;
            cur = u;
        }
        int u = p[cur].r;
        for (int i = 0; i < k; i++) putchar(p[u].s[i]);  //输出整块小部分
    }
}

void prev() {
    if (!y)  //块内下标无了，退到上一个块
        x = p[x].l, y = p[x].cnt - 1;
    else
        y--;
}

void next() {
    if (y >= p[x].cnt - 1)  //块内下标无了，进到下一个块
        x = p[x].r, y = 0;
    else
        y++;
}

int main(void) {
    n = read();
    for (int i = 1; i < maxn; i++) q[++idx] = i;
    str[0] = '>';//添加一个哨兵点
    insert(1);
    move(1);
    while (n--) {
        int a;
        char op[10];
        scanf("%s", op);
        if (!strcmp(op, "Move"))
            move((a = read()) + 1);
        else if (!strcmp(op, "Insert")) {
            a = read();
            int i = 0, k = a;
            while (a) {
                str[i] = getchar();
                if (check(str[i])) i++, a--;
            }
            insert(k);
            merge();
        } else if (!strcmp(op, "Delete")) {
            a = read();
            remove(a);
            merge();
        } else if (!strcmp(op, "Get")) {
            a = read();
            get(a);
            putchar('\n');
        } else if (!strcmp(op, "Prev"))
            prev();
        else
            next();
    }
    return 0;
}