【Coel.学习笔记】费用流的常见模型

哈啊……学完这部分就可以结束网络流了，好困困……

网格图模型

网格图模型的建图也是有一定套路的。
但要注意分辨用什么算法解决。例如之前提到的王者之剑，虽然也是网格图模型，但用到的是最小割。

方格取数加强版

洛谷传送门
有一个方格图，某些方格中填入正整数，而其他的方格中则放入数字 $0$。从图的左上角出发，可以向下行走，也可以向右走，直到到达右下角。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字 $0$）。总共走 $k$ 次，求出能够取到的最大值。

解析：这道题是经典老题方格取数的加强版，原题只会走两次，所以可以用动规求解。这题呢？对不起，动规时间复杂度 $O(2^kn^k)$，绝对会超时。

从网络流的角度思考问题。对于每个可行的路径都可以连一条边，容量为正无穷；再给起点和源点、终点和汇点连容量为 $k$ 的边，就得到了一个流网络。由于费用和点有关，还是用拆点法，在入点和出点之间连边。为了表示只能拿到一次数字，建两条边，一条容量为 1，费用等于点上数字；另一条容量正无穷，费用为 0。

现在这题就变成最大费用最大流了，直接求解即可。

inline int get(int x, int y, int inv) { return (x * n + y) * 2 + inv; }
//节点编号，inv 表示这个点是入点还是出点
int main(void) {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    memset(head, -1, sizeof(head));
    cin >> n >> k;
    S = 0, T = n * n * 2 + 1;
    add(S, get(0, 0, 0), k, 0);
    add(get(n - 1, n - 1, 1), T, k, 0);
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++) {
            int x;
            cin >> x;
            add(get(i, j, 0), get(i, j, 1), 1, x);
            add(get(i, j, 0), get(i, j, 1), inf, 0);
            if (i + 1 < n) add(get(i, j, 1), get(i + 1, j, 0), inf, 0);
            if (j + 1 < n) add(get(i, j, 1), get(i, j + 1, 0), inf, 0);
    }
    cout << Edmond_Karp();
    return 0;
}

网络流 24 题：深海机器人问题

洛谷传送门
潜艇内有多个深海机器人。

潜艇到达深海海底后，深海机器人将离开潜艇向预定目标移动。

深海机器人在移动中还必须沿途采集海底生物标本。

沿途生物标本由最先遇到它的深海机器人完成采集。

每条预定路径上的生物标本的价值是已知的，而且生物标本只能被采集一次。

本题限定深海机器人只能从其出发位置沿着向北或向东的方向移动，而且多个深海机器人可以在同一时间占据同一位置。若机器人不能到达终点则不能放置。

用一个 $P \times Q$ 网格表示深海机器人的可移动位置。

西南角的坐标为 $(0,0)$，东北角的坐标为 $(P,Q)$。

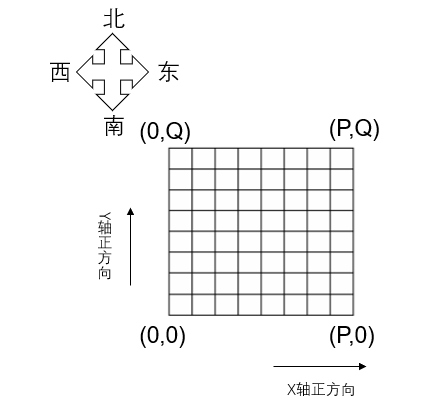
给定每个深海机器人的出发位置和目标位置，以及每条网格边上生物标本的价值。

计算深海机器人的最优移动方案，使尽可能多的深海机器人到达目的地的前提下，采集到的生物标本的总价值最高。

解析：题面很难简述，就直接抄下来了（

不难发现这是一个多源汇最大费用最大流问题，建立虚拟源点和虚拟汇点，源点与存在机器人的地方连边，容量等于 1；到达点与汇点连边，容量等于 1。中间可以走到的点再连边，由于每个标本只能拿一次，和上题一样建双边，一条容量无限费用 0，一条容量为 1 费用等于标本价值。

inline int get(int x, int y) {
    return x * (m + 1) + y;
}

int main(void) {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int St, Ed;
    cin >> St >> Ed >> n >> m;
    S = (n + 1) * (m + 1), T = S + 1;
    memset(head, -1, sizeof(head));
    for (int i = 0; i < n + 1; i++)
        for (int j = 0; j < m; j++) {
            int cost;
            cin >> cost;
            add(get(i, j), get(i, j + 1), 1, cost);
            add(get(i, j), get(i, j + 1), inf, 0);
        }
    for (int i = 0; i < m + 1; i++)
        for (int j = 0; j < n; j++) {
            int cost;
            cin >> cost;
            add(get(j, i), get(j + 1, i), 1, cost);
            add(get(j, i), get(j + 1, i), inf, 0);
        }
    for (int i = 1; i <= St; i++) {
        int x, y, k;
        cin >> k >> x >> y;
        add(S, get(x, y), k, 0);
    }
    for (int i = 1; i <= Ed; i++) {
        int x, y, k;
        cin >> k >> x >> y;
        add(get(x, y), T, k, 0);
    }
    cout << Edmond_Karp();
    return 0;
}

费用流的拆点

拆点是网络流里一个很重要的建图技巧，在费用流也一样。

网络流 24 题：餐巾计划问题/[HNOI2001]软件开发

洛谷传送门 + 双倍经验
一个餐厅在若干天内需要不等量的新毛巾，已知获得新毛巾的方式有三种：直接买新毛巾，把旧毛巾送到快洗店或是慢洗店，不同的方式花费时间与价格都不同。前一天获得的新毛巾不能留到下一天用，且每天的毛巾必须刚好为需要的毛巾。求出花费最小值。

解析：对三种情况分别建边。购买毛巾，则源点与新毛巾连边，容量无限费用等于新毛巾价格；送到店里，旧毛巾和恰好能运到的新毛巾连边，容量无限费用等于洗毛巾价格。
对于用完的旧毛巾和需要的新毛巾，分别和源点汇点相连，容量等于毛巾需求量，费用为 0。
此外一条旧毛巾还可以留到下一天，所以两天的旧毛巾连边，容量无限费用为 0。

signed main(void) {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> n;
    S = 0, T = n * 2 + 1;
    memset(head, -1, sizeof(head));
    for (int i = 1; i <= n; i++)
        cin >> r[i];
    cin >> ne >> fas >> fasc >> slo >> sloc; //新毛巾费用，快洗用时和花费，慢洗用时和花费
    for (int i = 1; i <= n; i++) {
        add(S, i, r[i], 0);
        add(n + i, T, r[i], 0);
        add(S, n + i, inf, ne);
        if (i < n) add (i, i + 1, inf, 0);
        if (i + fas <= n) add(i, n + i + fas, inf, fasc);
        if (i + slo <= n) add(i, n + i + slo, inf, sloc);
    }
    cout << Edmond_Karp();
    return 0;
}

费用流的上下界可行流

[NOI2008] 志愿者招募

洛谷传送门
有一个项目需要 $n$ 天完成，每天需要 $a_i$ 个志愿者，有 $m$ 种志愿者，每种志愿者可以在 $s_i$ 到 $t_i$ 天内工作，每人收费 $c_i$ 元。求完成项目的最小花费。

解析：点上表示人数有点困难，我们把它换到边上，用 $n$ 与 $n+1$ 号点之间的容量下界表示第 $n$ 天需要的志愿者。对于志愿者，从$t_i+1$ 到 $s_i$ 连边（相当于志愿者在这个区间循环流动），费用等于志愿者单价，容量正无穷。这样就变成了一个无源汇有上下界最小费用可行流问题（好吓人的名字）。因为没有源汇点，所以要手动加上虚拟的。

int main(void) {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> n >> m;
    S = 0, T = n + 2;
    memset(head, -1, sizeof(head));
    int lst = 0;
    for (int i = 1; i <= n; i++) {
        int num;
        cin >> num;
        if (lst > num) add(S, i, lst - num, 0);
        if (lst < num) add(i, T, num - lst, 0);
        add(i, i + 1, inf - num, 0);
        lst = num;
    }
    add(S, n + 1, lst, 0);
    for (int i = 1; i <= m; i++) {
        int l, r, cost;
        cin >> l >> r >> cost;
        add(r + 1, l, inf, cost);
    }
    cout << Edmond_Karp();
    return 0;
}