【Coel.学习笔记】最小割进阶：最大权闭合图与最大密度子图

又要学定义了，有点糟心……

新知详解

包括最大权闭合图与最大密度子图。

最大权闭合图

闭合图是有向图的一个点集，满足任何一个点的出边指向的点都属于这个点集中，也就是说出边不能跨集合。点集与点所连的边合称为闭合子图。

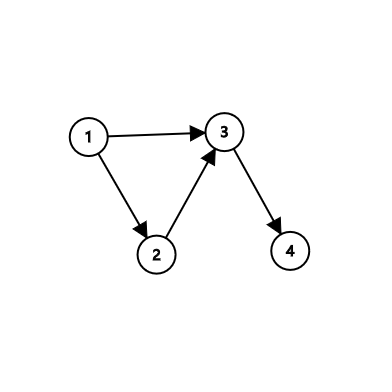
下图展示的例子中， \((1,3),(2,3),(1,2,3)\) 都不能构成一个闭合图，但 \((3,4)\) 可以构成一个闭合图。

最大权闭合图是点权和最大的闭合图。

求最大权闭合图，需要把这个问题对应到流网络的割集之中。

我们先试着把原图变成流网络。源点与所有点权为正的点连边，容量等于权值；汇点与所有点权为负的点连边，容量等于权值的相反数。对于原图存在的边，容量设为正无穷。

为了做法方便，我们定义一种特殊的割：
简单割：所有割边只为与源点和汇点所连边，不包含原图的边。由于中间的边容量已经为正无穷，所以最小割一定不会包含原图边。因此，最小割一定是一个简单割。

接下来证明闭合图能够和简单割一一对应，这样也就可以用最小割模型求解了。首先，对于原图的任何一个闭合点集，构造流网络的割集，使得割的 \(S\) 集合为源点加上闭合子图点，\(T\) 集合为流网络去掉 \(S\) 集合点。因为对于闭合子图任意一个点，能走到的点都处在这个点集之中，所以 \(S\) 集合必然是闭合的，\(T\) 集合同理，那么闭合图对应简单割；反过来，对于一个简单割，它对应的闭合子图是 \(S\) 减去源点，由于 \(S\) 是简单割，所以不存在从 \(S\) 到 \(T\) 的直接连边，因此简单割可以对应闭合图。

可以证明，最大权值和等于正权值之和减去最小割。

最大密度子图

给出一个无权值的有向图，从中选择一个点集 \(V^\prime\) 与边集 \(E^\prime\)，使得边集中边所连点在点集之中。
最大密度子图就是找到一种选择方式，使得边集大小与点集大小之比最大。

怎么做？联系上次的 0/1 分数规划问题，转化为找到一个最大的 \(\lambda=\dfrac{|E^\prime|}{|V^\prime|}\)，等价于 \(|E^\prime|-\lambda|V^\prime|=0\)。求解左边式子最大值，若大于 \(0\) 则二分右半区间，反之二分左半区间。

怎么把问题划归为流网络模型？经过非常复杂的一番推导（这里就不写了）可以知道，这个问题可以转化为求 \(c_{S,T}\) 最小值，即最小割。

建图方式为：对于每次二分得到的 \(\lambda\)，统计每点的度数 \(deg_i\)，给源点与所有点连上容量等于总边数 \(m\) 的边，汇点连上容量等于 \(m+\lambda * 2 - deg_i\) 的边，最后再给每个点之间两两连边。

例题讲解

[NOI2006]最大获利（最大权闭合图做法）

洛谷传送门
有若干的地址可以建造通讯站，在某个点建造通讯站的成本为 \(P_i\)。若干个用户群要在两个通讯站 \(A_i,B_i\) 沟通，公司可以获利 \(C_i\)。求出最大利润（获利总和减去建通讯站花费）。

解析：把建站看做负权点，用户群看做正权点，这个问题就转化为最大权闭合图问题。源点与用户群连边，汇点与通讯站连边，再在用户群与对应的通讯站连边，求正权值之和减去最小割即可。
实际上，这题的点具有特殊性（每个用户群只会与两个通讯站相连），所以用最大权闭合图模型不是最优解。使用最大密度子图模型可以实现更优解。
代码如下（缩短一下篇幅，以后只放主函数内容了，反正最大流算法都一样）：

// Problem: P4174 [NOI2006] 最大获利
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4174
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Author:Coel
// 
// Powered by CP Editor (https://cpeditor.org)

/*省略了加边函数、dinic 的实现*/

int main(void) {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> n >> m;
    S = 0, T = n + m + 1;
    memset(head, -1, sizeof(head));
    for (int i = 1, p; i <= n; i++) {
        cin >> p;
        add(m + i, T, p);
    }
    for (int i = 1; i <= m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        add(S, i, c), add(i, m + a, inf), add(i, m + b, inf);
        sum += c;
    }
    cout << sum - dinic();
    return 0;
}

POJ3155 Hard Life

洛谷传送门
已知公司中一共有 \(n\) 名员工，员工之间共有 \(m\) 对两两矛盾关系，团队的管理难度系数等于团队中的矛盾关系对数除以团队总人数。找出一个安排方案，使得管理难度系数最大。
解析：最大密度子图的模板题，不过要输出方案。
输出方案的话，只要从源点跑一遍 dfs 就行了。
代码如下（这题用到了二分，dinic 实现有些许不同，所以完整放上）：

// Problem: UVA1389 Hard Life
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/UVA1389
// Memory Limit: 0 MB
// Time Limit: 3000 ms
// Author:Coel
//
// Powered by CP Editor (https://cpeditor.org)

#include <cstdlib>
#include <cstring>
#include <iostream>
#include <queue>

using namespace std;

const int maxn = 1e5 + 10, inf = 1e8;
const double eps = 1e-8;

int n, m, S, T;
int head[maxn], nxt[maxn], to[maxn], cnt;
double c[maxn];
int d[maxn], cur[maxn], deg[maxn];
int ans;
bool vis[maxn];

struct node {
    int u, v;
} e[maxn];

void add(int u, int v, double w1, double w2) {
    nxt[cnt] = head[u], to[cnt] = v, c[cnt] = w1, head[u] = cnt++;
    nxt[cnt] = head[v], to[cnt] = u, c[cnt] = w2, head[v] = cnt++;
}

bool bfs() {
    queue<int> Q;
    memset(d, -1, sizeof(d));
    Q.push(S), d[S] = 0, cur[S] = head[S];
    while (!Q.empty()) {
        int u = Q.front();
        Q.pop();
        for (int i = head[u]; ~i; i = nxt[i]) {
            int v = to[i];
            if (d[v] == -1 && c[i] > 0) {
                d[v] = d[u] + 1;
                cur[v] = head[v];
                if (v == T) return true;
                Q.push(v);
            }
        }
    }
    return false;
}

double find(int u, double limit) {
    if (u == T) return limit;
    double flow = 0;
    for (int i = cur[u]; ~i && flow < limit; i = nxt[i]) {
        int v = to[i];
        cur[u] = i;
        if (d[v] == d[u] + 1 && c[i] > 0) {
            double t = find(v, min(c[i], limit - flow));
            if (t <= 0) d[v] = -1;
            c[i] -= t, c[i ^ 1] += t, flow += t;
        }
    }
    return flow;
}

void dfs(int u) {
    vis[u] = true;
    if (u != S) ans++;
    for (int i = head[u]; ~i; i = nxt[i]) {
        int v = to[i];
        if (!vis[v] && c[i] > 0) dfs(v);
    }
}

void init_k(double k) {
    memset(head, -1, sizeof(head));
    cnt = 0;
    for (int i = 0; i < m; i++) add(e[i].u, e[i].v, 1, 1);
    for (int i = 1; i <= n; i++) {
        add(S, i, m, 0);
        add(i, T, m + k * 2 - deg[i], 0);
    }
}

double dinic(double k) {
    init_k(k);
    double res = 0, flow;
    while (bfs())
        while ((flow = find(S, inf))) res += flow;
    return res;
}

int main(void) {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    while (cin >> n >> m) {
        memset(deg, 0, sizeof(deg));
        ans = 0;
        S = 0, T = n + 1;
        for (int i = 0; i < m; i++) {
            int u, v;
            cin >> u >> v;
            deg[u]++, deg[v]++;
            e[i].u = u, e[i].v = v;
        }
        double l = 0, r = m;
        while (r - l > eps) {
            double mid = (l + r) / 2;
            double t = dinic(mid);
            if (m * n - t > 0)
                l = mid;
            else
                r = mid;
        }
        dinic(l);
        dfs(S);
        if (!ans) {
            cout << 1 << '\n' << 1 << '\n';
            continue;
        }
        cout << ans << '\n';
        for (int i = 1; i <= n; i++)
            if (vis[i]) cout << i << '\n';
        cout << '\n';
    }
    return 0;
}