python学习05

阶跃函数与sigmoid函数比较

不同点

• sigmoid函数的平滑性对神经网络的学习具有重要意义
• 感知机中神经元之间流动的是0或1的二元信号，而神经网络中流动的是连续的实数值信号

相同点

• 两者的结构均是“输入小时，输出接近0（为0）；随着输入增大，输出向1靠近（变成1）”输出信号的值都在0到1之间
• 两者均为非线性函数。sigmoid函数是一条曲线，阶跃函数是一条像阶梯一样的折线

函数本来是输入某个值后会返回一个值的转换器

• 神经网络的激活函数必须使用非线性函数，因为如果使用线性函数，加深神经网络的层数就没有意义了
• 线性函数的问题在于，不管如何加深层数，总是存在与之等效的“无 隐藏层的神经网络”。为了具体地（稍微直观地）理解这一点，我们来思 考下面这个简单的例子。这里我们考虑把线性函数h(x) = cx作为激活 函数，把y(x) = h(h(h(x)))的运算对应3层神经网络A。这个运算会进行 y(x) = c×c×c×x的乘法运算，但是同样的处理可以由y(x) = ax（注意， a = c 3）这一次乘法运算（即没有隐藏层的神经网络）来表示。如本例所示， 使用线性函数时，无法发挥多层网络带来的优势。因此，为了发挥叠加层所 带来的优势，激活函数必须使用非线性函数。

ReLU函数

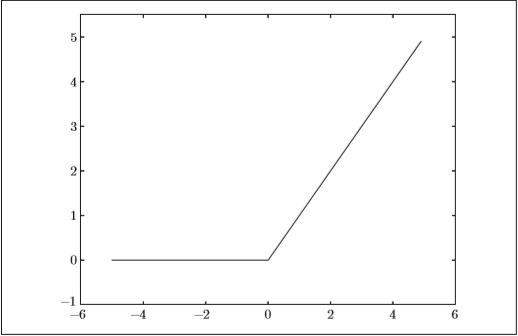
• ReLU函数在输入大于0时，直接输出该值；在输入小于等于0时，输 出0
  
  

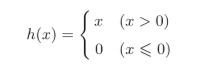
多维数组的运算

• 多维数组就是“数字的集合”

矩阵乘法

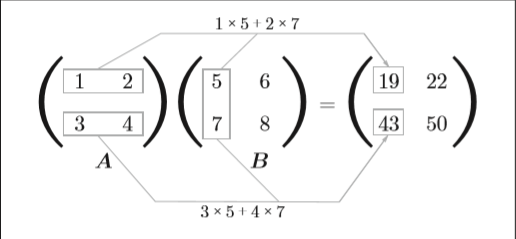
• 矩阵的乘积是通过左边矩阵的行（横向）和右边矩阵的列（纵 向）以对应元素的方式相乘后再求和而得到的。并且，运算的结果保存为新 的多维数组的元素。比如，A的第1行和B的第1列的乘积结果是新数组的 第1行第1列的元素，A的第2行和B的第1列的结果是新数组的第2行第1 列的元素。

• A第一行分别与B第一列乘积相加得到C第一行第一列

神经网络的内积