信号波峰波谷二阶差分识别算法
https://mp.weixin.qq.com/s/LQCfzSrnXU69MTVlTmXwEg
正文部分
1
波峰波谷用处
对于信号波峰波谷识别在嵌入式领域应该是非常广泛的,因为大部分的信号都处于一种时变的状态,信号在时域上处于一种类似于正弦波的波动状态。比如计步软件就是通过IMU模块所采集的变化的波形状态来识别波峰波谷,最终估算你所走过步数;
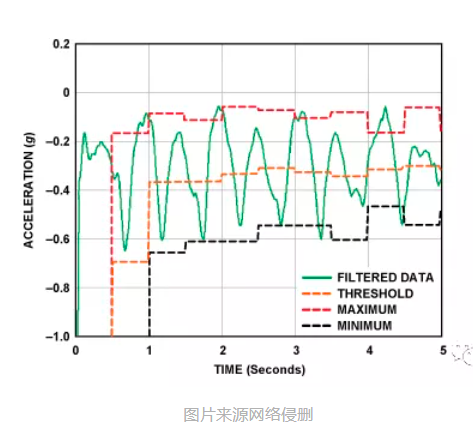
图片来源网络侵删上图显示了一个典型的x-, y-和z-测量模式,对应于一个跑步者的垂直,向前和侧面加速度。无论如何佩戴计步器,至少有一个轴会有相对较大的周期性加速度变化,因此通过检测其波峰波谷等算法即可对于检测步行或跑步的单位周期至关重要。
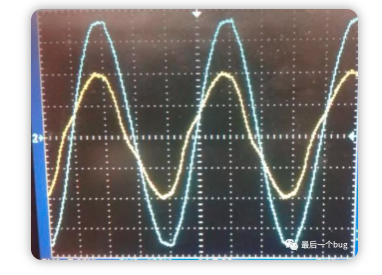
还有在电力系统中的交流电压电流,我们需要通过检测波峰波谷来确定电压电流在交流周期中的最大最小值,从而动态调节系统参数来达到自适应的目的,所以波峰波谷的检测是非常有用的。
2
比较法识别
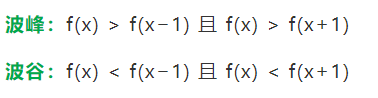
常规的设计办法为比较法 : 其中x表示当前采样点波峰:f(x) > f(x−1) 且 f(x) > f(x+1)波谷:f(x) < f(x−1) 且 f(x) < f(x+1)
然而这样识别对于没有什么噪声,且每个采样点为不同的信号来说还是合适的,但在严苛的环境中还需要构造更多的判断条件来进行一些错误判断的规避,终究还是麻烦了一些,并且容易遗漏。
3
差分识别
在学生阶段我们就学习了导数的概念,如果一个函数一阶导数左右异号,那分别就是波峰或者波谷。而对于数字信号的处理通过采样都会变成离散信号,信号对时间的微分在离散域内即为差分。在进行波形识别之前数据采集是必不可少的,其中最重要的是采样速率和精度,以便从采样信号中不失真的恢复原连续信号。(香农采样)采样的过程中由于电子器件的杂讯等,数据难免会引入噪声,为了简化识别算法一般都会进行滤波处理,比如一些平滑处理等,然后才开始波峰波谷识别。
A
识别算法过程
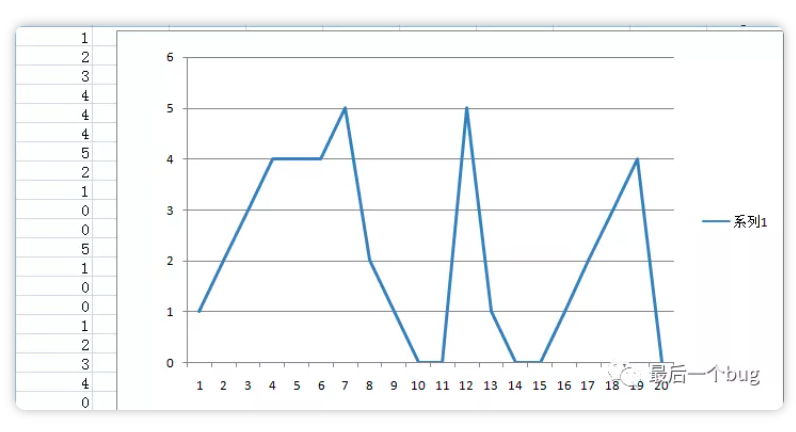
1、获得采样点序列

2、进行差分处理
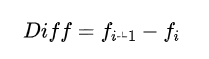
3、由于不在乎具体的差分幅值,把所有数据归一到-1,0,1
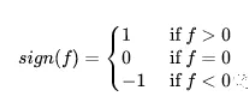
4、差分值为0的点即为相同点,如果使用比较法则峰值检测可能失效,便需要更多的条件,而这里我们直接把相同点0置为前一个非0即可规避该问题。
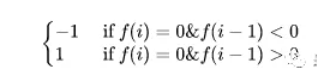
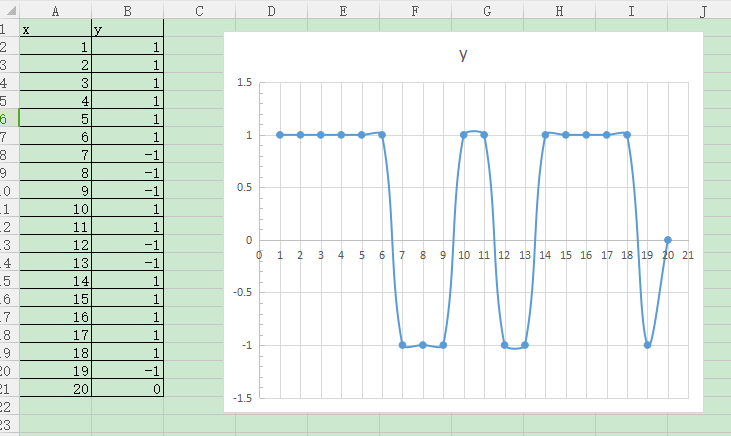
5、最终Diff再次进行差分,-2/+2即为波峰/波谷。
#include <stdio.h>
#include <stdlib.h>
#define SAMPLE_MAX 20
#define PV_MAX 10
int Sample[SAMPLE_MAX] = {1, 2, 3, 4, 4, 4, 5, 2, 1, 0, 0, 5, 1, 0, 0, 1, 2, 3, 4, 0};
int SampleDiff[SAMPLE_MAX] = {0};
typedef struct _tag_FindPV
{
int Pos_Peak[PV_MAX]; //波峰位置存储
int Pos_Valley[PV_MAX]; //波谷位置存储
int Pcnt; //所识别的波峰计数
int Vcnt; //所识别的波谷计数
} SFindPV;
SFindPV stFindPV;
/********************************************
* Fuction : initialFindPV
* Note : 初始化相关数据
*******************************************/
void initialFindPV(void)
{
int Index = 0;
for (Index = 0; Index < SAMPLE_MAX; Index ++)
{
SampleDiff[Index] = 0;
}
for (Index = 0; Index < PV_MAX; Index ++)
{
stFindPV.Pos_Peak[Index] = -1;
stFindPV.Pos_Valley[Index] = -1;
}
stFindPV.Pcnt = 0;
stFindPV.Vcnt = 0;
}
/********************************************
* Fuction : FindPV
* Note : 找波峰波谷
*******************************************/
void FindPV(SFindPV *pFindPV, float *Sample)
{
int i = 0;
//step 1 :首先进行前向差分,并归一化
for (i = 0; i < SAMPLE_MAX - 1; i++)
{
if (Sample[i + 1] - Sample[i] > 0)
{
SampleDiff[i] = 1;
}
else if (Sample[i + 1] - Sample[i] < 0)
{
SampleDiff[i] = -1;
}
else
{
SampleDiff[i] = 0;
}
}
for (int i = 0; i < SAMPLE_MAX; i++)
{
printf("diff[%d] = %d \t", i, SampleDiff[i]);
if ( ((i + 1) & 0x03) == 0)
{
printf("\n");
}
}
//step 2 :对相邻相等的点进行领边坡度处理
for (i = 0; i < SAMPLE_MAX - 1; i++)
{
if (SampleDiff[i] == 0)
{
if (i == (SAMPLE_MAX - 2))
{
if (SampleDiff[i - 1] >= 0)
{
SampleDiff[i] = 1;
}
else
{
SampleDiff[i] = -1;
}
}
else
{
if (SampleDiff[i + 1] >= 0)
{
SampleDiff[i] = 1;
}
else
{
SampleDiff[i] = -1;
}
}
}
}
printf("\n");
for (int i = 0; i < SAMPLE_MAX; i++)
{
printf("diff2[%d] = %d \t", i, SampleDiff[i]);
if ( ((i + 1) & 0x03) == 0)
{
printf("\n");
}
}
//step 3 :对相邻相等的点进行领边坡度处理
for (i = 0; i < SAMPLE_MAX - 1; i++)
{
if (SampleDiff[i + 1] - SampleDiff[i] == -2) //波峰识别
{
pFindPV->Pos_Peak[pFindPV->Pcnt] = i + 1;
pFindPV->Pcnt++;
}
else if (SampleDiff[i + 1] - SampleDiff[i] == 2) //波谷识别
{
pFindPV->Pos_Valley[pFindPV->Vcnt] = i + 1;
pFindPV->Vcnt++;
}
}
for (int i = 0; i < SAMPLE_MAX; i++)
{
printf("pFindPV->Pos_Valley[%d] = %d \t", i, pFindPV->Pos_Valley[i]);
printf("pFindPV->Pos_Peak[%d] = %d \t", i, pFindPV->Pos_Peak[i]);
if ( ((i + 1) & 0x01) == 0)
{
printf("\n");
}
}
}
/********************************************
* Fuction : main
* Note : 模拟查找波峰波谷
*******************************************/
int main(int argc, char *argv[])
{
int i = 0;
initialFindPV();
FindPV(&stFindPV, Sample);
printf("Peak\n");
for (i = 0 ; i < stFindPV.Pcnt; i++)
{
printf("-%d", stFindPV.Pos_Peak[i] + 1); //加1是为了与上图横坐标一致
}
printf("\nValley\n");
for (i = 0 ; i < stFindPV.Vcnt; i++)
{
printf("-%d", stFindPV.Pos_Valley[i] + 1);
}
printf("\n\n");
printf("欢迎关注:最后一个bug\n");
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号