如何用adc的芯片来强化学习——二进制的补码

部分参考了https://www.cnblogs.com/songdechiu/p/5397070.html

一、补码的优点

1、可以将减法转化为加法，在计算机中只保留加法

2、将符号位参与运算

二、如何实现？

我们先以钟表为例子，假设现在的标准时间为4点整，而有一个钟的时间为7点整。我们可以将时针逆时针旋转3格，或者将时针顺时针旋转9格，如图。

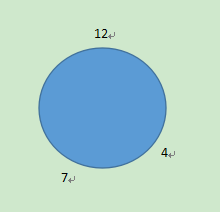
7-3=7+9=4　　mod（12）

上述式子为一个同余式，同余式的标准定义为

a ≡b (mod n) 

即同余式两边的数值，对n进行取余后的数值相等。

从上述例子我们可以得到灵感，即用一个正数来替代负数（上述例子中用9替代-3）从而将减法转化为加法。

 

在计算机中，我们应该如何进行这种替换？

我们应先明确一些概念，如原码表示，加法器的溢出，负数取余。

 

原码表示：最高位为符号位

正数：符号位为0，剩余的为数值

如用8位表示一个数，则+8为 0000 1000_（2）

负数：符号位为1，剩余的为数值

如用8位表示一个数，则-8为 1000 1000_（2）

采用原码来进行计算机的运算，将会非常复杂，因为将会有很多逻辑判断。

如两数相加时，同好则数值相加；不同号则相减，而且还要比较数值部分的绝对值的大小。

所以人们找到了补码的表示方法。

 

加法器的溢出：

假如一个加法器为8位的加法器，当和的值超过了 1111 1111_（2），那么高位将被丢弃。

如 1111 1111_（2）+ 1111 1111_（2）= 1111 1110_（2）

也就是说这个加法器只能表示0-255，即256为一个轮回，从我们的角度来看的话，这个加法器对结果进行取余，其模为256。

让我们推广到一般情况，n位加法器

x_nx_n-1……x₀，即只能表示0-2ⁿ-1，即2ⁿ为一个轮回，从我们的角度来看的话，这个加法器对结果进行取余，其模为2ⁿ。

（原文有错误，因此标红颜色，这里已经修改）及256一个轮回，即2的8次为一个轮回，而不是

负数的取模：

 我们应该先探讨一下负数的取模操作，我们知道取模公式如下所示：

x mod y = x - y* [x/y]

注：[x/y]为下取整符号

 

上边我们说到要用正数来取代负数从而达到，将减法转化为加法，那么应该怎么取代，关系式是怎么样的？

 对于一般二进制数x_nx_n-1……x₀进行探讨，从上边的讨论我们知道，对这个二进制数进行加减操作时，最终的结果都将进行模为2ⁿ的取余操作。我们假设这个二进制数值为[x]_补，其代表的真值为x。

1、当x_n为0时，[x]_补=x，范围为0 - 2^n-1；即0~127是整数

2、当x_n为1时，其代表的为负数x，我们知道这里应该用一个正数[x]_补来取代负数x，并且使模为2ⁿ的同余式相等。

让我们先来讨论-1，-1对2ⁿ进行取余，即

-1 mod 2ⁿ = -1 - 2ⁿ*(-1) = 2ⁿ- 1

[2ⁿ - 1]_补 = -1

所以我们用2ⁿ - 1替代-1 举例2^8-1=255,11111111 代表-1，可以从ads1259的datasheet中看出端倪

 

则，对负数x为，

x mod 2ⁿ = x - 2ⁿ*(-1) = 2ⁿ + x

[2ⁿ + x]_补 = x

x的范围为-1至-2^n-1

，即-1到-128

所以我们用2ⁿ - 1替代x

——以补码定义式为基础，沿数轴列出典型的真值、原码与补码表示，可清楚了解补码的有关性质——

 

这就是为什么8位二进制, 使用原码或反码表示的范围为[-127, +127], 而使用补码表示的范围为[-128, 127].

因为机器使用补码, 所以对于编程中常用到的32位int类型, 可以表示范围是: [-2³¹, 2³¹-1] 因为第一位表示的是符号位.而使用补码表示时又可以多保存一个最小值.  

总结：这里可以根据很多adc的芯片来进行学习二进制的补码，很多能够采集正负电压的adc芯片都采用二进制的补码来表示。

比如在ti的ads1118中，有如下温度传感器的采集数据说明

 以及

 很简单，如何得到负数的温度（LSB），可以这么计算，因为这个温度传感器adc的精度是14位，最高位是符号位，假如采集得到寄存器是0x3ce0，那么，我们可以这么计算真正的负数大小：0x4000-0x3ce0=0x320，说明有这么多付的LSB，因此，还是比较简单的，

同样，ads1259上面，-1是用ffffff来表示的，那么0x1000000-0xFFFFFF=1，说明是一个LSB。