补码复习
https://www.douban.com/note/223507364/
这些文章也挺好的。。
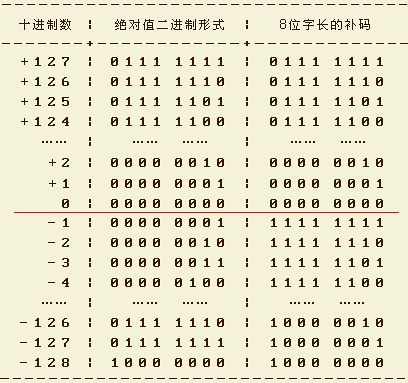
| 十进制数 | 符号位+ 二进制绝对值 的表示方式 | ones' complement | two's complement |
| +7 | 0111 | 表示方式不变 | 表示方式不变 |
| +6 | 0110 | 表示方式不变 | 表示方式不变 |
| +5 | 0101 | 表示方式不变 | 表示方式不变 |
| +4 | 0100 | 表示方式不变 | 表示方式不变 |
| +3 | 0011 | 表示方式不变 | 表示方式不变 |
| +2 | 0010 | 表示方式不变 | 表示方式不变 |
| +1 | 0001 | 表示方式不变 | 表示方式不变 |
| +0 | 0000 | 表示方式不变 | 表示方式不变 |
| -0 | 1000 | 1111 | [1]0000 |
| -1 | 1001 | 1110 | 1111 |
| -2 | 1010 | 1101 | 1110 |
| -3 | 1011 | 1100 | 1101 |
| -4 | 1100 | 1011 | 1100 |
| -5 | 1101 | 1010 | 1011 |
| -6 | 1110 | 1001 | 1010 |
| -7 | 1111 | 1000 | 1001 |
| -8 | 超出4个bit所能表达范围 | 超出4个表达范围 | 1000 |
| 注: | 要设计硬件区分符号位,比较绝对值大小。 | 无需设计硬件比较大小,但零存在两种表示方法。 |
较好的解决上述问题
。由于零只有一种表达方式,所以,可以比别的方式多表达一个-8.
|
截图百度百科的,我们使用第二种补码的格式,就是后面的那种。
参考了知乎的解答~~https://www.zhihu.com/question/20159860
链接:https://www.zhihu.com/question/20159860/answer/21113783
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
复习c++的时候遇到二进制编码问题,上网搜索了一番,终于有点眉目。 一般来说,初学二进制编码时,会看到如下描述:
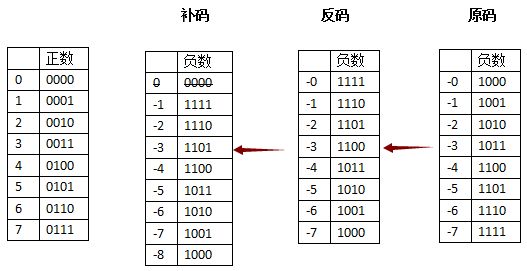
原码表示法是机器数的一种简单的表示法。其符号位用0表示正号,用:表示负号,数值一般用二进制形式表示。
机器数的反码可由原码得到。如果机器数是正数,则该机器数的反码与原码一样;如果机器数是负数,则该机器数的反码是对它的原码(符号位除外)各位取反而得到的。
机器数的补码可由原码得到。如果机器数是正数,则该机器数的补码与原码一样;如果机器数是负数,则该机器数的补码是对它的原码(除符号位外)各位取反,并在未位加1而得到的。
如果是为了考试,死记即可。但我总想搞清楚为什么计算机里面的数要这样子表达?意义何在?-128的补码为什么是10000000?为什么补码有这么奇怪的运算规则?计算机算减法的时候都需要从源码到补码的计算吗?
思路
google了一下,看到了这样一篇文章,注意到文中关于补码来历的描述,可以总结如下:
- 计算机里面,只有加法器,没有减法器,所有的减法运算,都必须用加法进行。
- 用补数代替原数,可把减法转变为加法。出现的进位就是模,此时的进位,就应该忽略不计。
- 二进制下,有多少位数参加运算,模就是在 1 的后面加上多少个 0。
- 补码就是按照这个要求来定义的:正数不变,负数即用模减去绝对值。
补充解释一下“模”的概念(不准确):
考虑时钟上时间的计算,假设现在时针指向数字3,若问“6小时前时针指向的数字是几”,则可以:
1. 将时针逆时针拨动6格。
2. 将时针顺时针拨动12 - 6 = 6格。
两者的结果是一样的。这里称12为“模”。
故有 3时 - 6个小时 = 3时 + (12 - 6个小时),这里可以看到将减法转换成加法的过程,即“加上模减去绝对值的差”。
所以,假设模是10,有效位数为1,当我们计算 9 - 7 的时候:
9 - 7 => 9 + (10 - 7) = 12,去掉最高的位后,得到2,这是正确的结果。
从9 - 7 = 2 和 9 + (10 - 7) = 12可以凭后者比前者多“1”来看出前者中“7”的正负号。
作者的意思是说,计算机里面所有数都以补码形式保存,加减运算都是补码之间的加法运算。然后作者提出了一个我之前没听过的观点:
补数 和 补码的定义式 里面,根本就没有什么符号位。这最高位的1、0是自然出现的,并不是由人来规定的。
的确,符号位在补码运算里面是“模”,本身并不带符号的意义。因为计算机将加法转换成加上一个“负数”,而负数又以补码的形式表现。补码比源码多一位,从这多出来的一位可以推断出原来数字的正负号,所以成为了符号位。也可以这样认为,留出一位(不全部占满)的原因是要用“模”来表示正负数。
也就是说,不是特意留出一个符号位,用1和0来表示正负号。而是补码运算可以用最高位来表示正负,所以符号位诞生了。
那么为什么-128的补码是10000000?可以这样理解。-128是一个负数,所以它的补码是它的“模”减去它的绝对值,即:
100000000 - 10000000 = 10000000那么为什么负数补码等于源码的反码加一呢?可以这样推导:
100000000 - 10000000
= (11111111 + 00000001) - 10000000
= 11111111 - 10000000 + 1
= 01111111 + 1 //反码加一
= 10000000由此我们得知,在计算机里面所有的数字都以补码形式存储。127存成01111111,-127存成11111111,算减法就变成算加法了,尽管你看到的是“-”号。
-------
今天读《计算机组成-结构化方法》后,对这个问题有了新的理解。
将负数用补码表示,实际上是实现了一种从[-128, 127]到[0, 255]的映射。如下所示:
+----------------------------+
| 255 -1 11111111 |
| 254 -2 11111110 |
| 253 -3 11111101 |
| 252 -4 11111100 |
| 251 -5 11111011 |
| 246 -10 11110110 |
| 236 -20 11101100 |
| 226 -30 11100010 |
| 216 -40 11011000 |
| 206 -50 11001110 |
| 196 -60 11000100 |
| 186 -70 10111010 |
| 156 -100 10011100 |
| 129 -127 10000001 |
| 128 -128 10000000 |
| 127 127 01111111 |
| 100 100 01100100 |
| 70 70 01000110 |
| 60 60 00111100 |
| 50 50 00110010 |
| 40 40 00101000 |
| 30 30 00011110 |
| 20 20 00010100 |
| 10 10 00001010 |
| 5 5 00000101 |
| 4 4 00000100 |
| 3 3 00000011 |
| 2 2 00000010 |
| 1 1 00000001 |
| 0 0 00000000 |
+----------------------------+



 浙公网安备 33010602011771号
浙公网安备 33010602011771号