手写Pascal解释器(三)
一、part7
资料来源:https://ruslanspivak.com/lsbasi-part7/

看作者博客的标题就知道,这一节我们需要完成抽象语法树的功能。
抽象语法树和具体语法树(解析树)
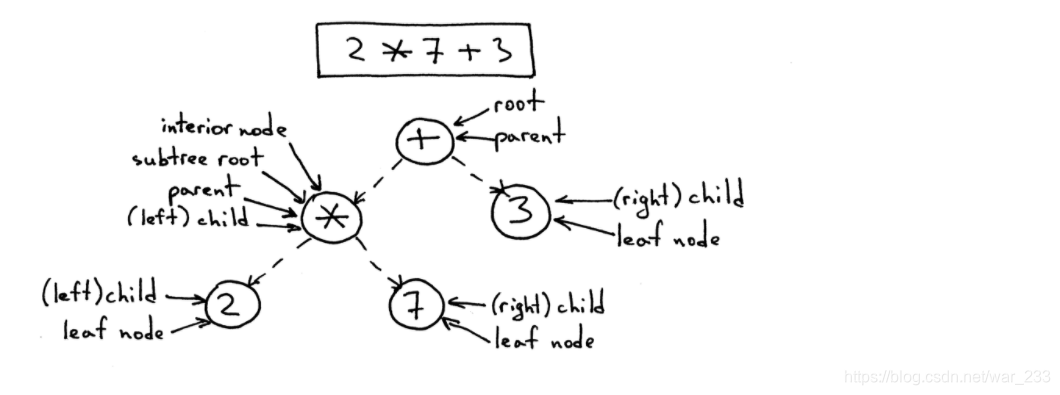
例如这个表达式的例子(2 * 7 + 3)就形成了这样的一棵抽象语法树。
而该表达式的解析树(具体语法树)如下图所示:
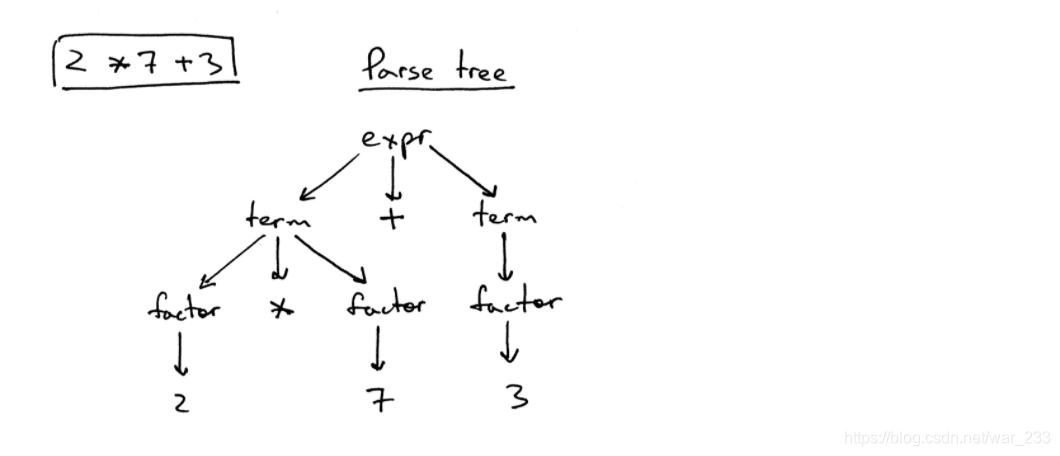
- 解析树记录了解析器应用于识别输入的一系列规则。
- 语法分析树的根标有语法开始符号。
- 每个内部节点代表一个非终结符,也就是说,它代表一个语法规则应用程序,例如本例中的expr,term或factor。
- 每个叶节点代表一个Token。
两者的区别:
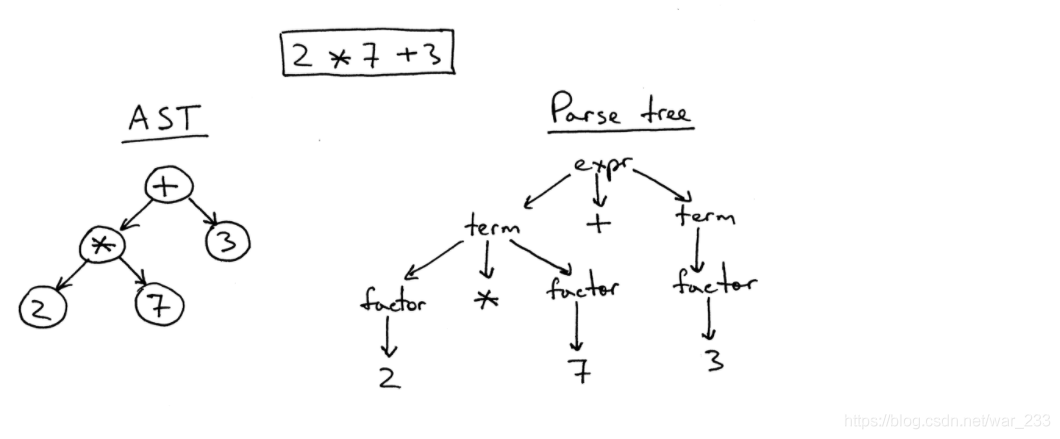
- AST使用运算符/操作作为根节点和内部节点,并使用操作数作为其子节点。
- 与解析树不同,AST不使用内部节点表示语法规则。
- AST不能代表真实语法中的每个细节(这就是为什么它们被称为abstract)的原因,例如,没有规则节点也没有括号。
- 与相同语言结构的分析树相比,AST的密度更高。
如何在AST中对运算符优先级进行编码?
In order to encode the operator precedence in AST, that is, to represent that “X happens before Y” you just need to put X lower in the tree than Y. And you’ve already seen that in the previous pictures.
为了在AST中编码运算符优先级,即表示“ X发生在Y之前”,您只需要在树中将X放到比Y低的位置即可。并且您已经在上一张图片中看到了。
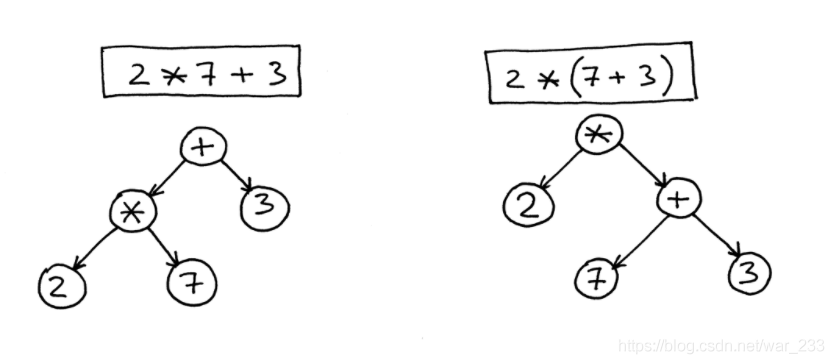
代码实现
先编写抽象语法树接口 AST
public interface AST {
}
(它确实是一个空接口,只是为了实现多态)
二元运算符节点:
public class BinOp implements AST {
public Token op;
public AST left;
public AST right;
public BinOp(AST left, Token op, AST right){
this.left = left;
this.op = op;
this.right = right;
}
}
数字(整数)节点:
public class Num implements AST {
public Token token;
public int value;
public Num(Token token){
this.token = token;
this.value = (Integer) token.value;
}
}
原有的Lexer类不做改变(原来也已经说明过,Lexer类的职责是读取字符串并将它分解为各个Token)。
新增Parser类(语法解析器类,生成抽象语法树):
(把原来的Interpreter类的一些功能划分到了它的身上,原来是返回各个部分的值,而这个时候返回各个部分合成的解析树)
public class Parser {
private final Lexer lexer;
private Token currentToken;
public Parser(Lexer lexer) throws Exception {
this.lexer = lexer;
this.currentToken = this.lexer.getNextToken();
}
private void error() throws Exception {
throw new Exception("Invalid syntax");
}
private void eat(Token.TokenType tokenType) throws Exception {
if (currentToken.type == tokenType){
currentToken = lexer.getNextToken();
}
else {
this.error();
}
}
private AST factor() throws Exception {
// factor : INTEGER | LPAREN expr RPAREN
Token token = currentToken;
if (currentToken.type == Token.TokenType.INTEGER){
eat(Token.TokenType.INTEGER);
return new Num(token);
}
else {
eat(Token.TokenType.LPAREN);
AST result = expr();
eat(Token.TokenType.RPAREN);
return result;
}
}
private AST term() throws Exception {
// term : factor ((MUL | DIV) factor)*
AST node = factor();
while (currentToken.type == Token.TokenType.MUL || currentToken.type == Token.TokenType.DIV){
Token token = currentToken;
if (token.type == Token.TokenType.MUL){
eat(Token.TokenType.MUL);
}
else {
eat(Token.TokenType.DIV);
}
node = new BinOp(node, token, this.factor());
}
return node;
}
private AST expr() throws Exception {
/*
expr : term ((PLUS | MINUS) term)*
term : factor ((MUL | DIV) factor)*
factor : INTEGER | LPAREN expr RPAREN
*/
AST node = term();
while (currentToken.type == Token.TokenType.PLUS || currentToken.type == Token.TokenType.MINUS){
Token token = currentToken;
if (token.type == Token.TokenType.PLUS){
eat(Token.TokenType.PLUS);
}
else {
eat(Token.TokenType.MINUS);
}
node = new BinOp(node, token, term());
}
return node;
}
public AST parse() throws Exception {
return this.expr();
}
}
parser类接受一个lexer对象,职责是接收lexer对象将字符串转化为的多个token,输出表达式对应的抽象语法树AST。
NodeVisitor类,访问各个AST节点的基类(使用反射进行实现)
public abstract class NodeVisitor {
// 调用visit方法时,先使用反射得到AST子类具体的类名,即className,
// 然后调用"visit"+className的方法,如若node为BinOp,则调用visitBinOp()方法
// 使用反射大大提高了编码实现的灵活性
protected int visit(AST node) throws Exception {
String[] strings = node.getClass().getName().split("\\.");
String className = strings[strings.length-1];
Method visitMethod = this.getClass().getDeclaredMethod("visit"+className, AST.class);
return (int) visitMethod.invoke(this, node);
}
protected void genericVisit() throws Exception {
throw new Exception("No this type to visit");
}
// 写好访问各个节点的接口方法,供实现类来实现
abstract int visitBinOp(AST node) throws Exception;
abstract int visitNum(AST node);
}
该类的职责是定义AST visitor需要完成的接口,以及使用反射使访问多种类型的AST变得简单。
最后是Interpreter类:
public class Interpreter extends NodeVisitor {
// 成员变量parser
private final Parser parser;
public Interpreter(Parser parser){
this.parser = parser;
}
@Override
protected int visitBinOp(AST node) throws Exception {
BinOp binOp = (BinOp)node;
int res = 0;
switch (binOp.op.type){
case PLUS:
res = visit(binOp.left) + visit(binOp.right);
break;
case MINUS:
res = visit(binOp.left) - visit(binOp.right);
break;
case MUL:
res = visit(binOp.left) * visit(binOp.right);
break;
case DIV:
res = visit(binOp.left) / visit(binOp.right);
break;
}
return res;
}
@Override
protected int visitNum(AST node) {
return ((Num)node).value;
}
public int interpret() throws Exception {
AST tree = parser.parse();
return this.visit(tree);
}
}
Interpreter类的接收一个parser对象,其对应的职责是接收parser对象调用parser后得到的AST,即抽象语法树,然后遍历抽象语法树的各个节点,最后将语法树所代表的表达式的值输出出来。
总结各个类的职责(摘自大佬博客):
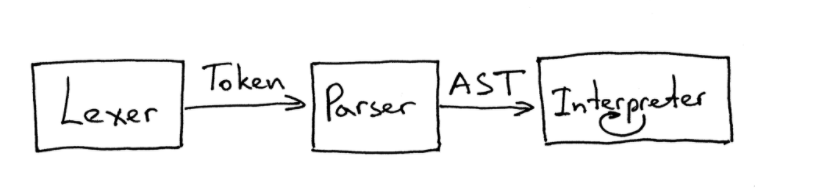
客户端类Main:
public class Main {
public static void main(String[] args) throws Exception {
Scanner scanner = new Scanner(System.in);
while (true) {
System.out.print("spi> ");
String text = scanner.nextLine();
if (text.equals("exit"))
break;
Lexer lexer = new Lexer(text);
Parser parser = new Parser(lexer);
Interpreter interpreter = new Interpreter(parser);
int res = interpreter.interpret();
System.out.println("res: " + res);
}
}
}
运行结果:

二、part8
资料来源:https://ruslanspivak.com/lsbasi-part8/
这一part我们主要要完成一元运算符的功能,在我们之前看起来好像已经完成了计算加减乘除表达式的所有功能,实际上我们还无法计算像这样一些表达式:+1 -3,(-1)*4,(-2-3) * (+4-5)等等这些带正负号的数,这一节我们就是为了解决正负号这种一元操作符无法表达的问题。
修改或新增的类:
由于我们只是增加一个新语法,所以词法解析器Lexer的代码是完全不用修改的,主要需要修改Parser和添加一个AST的子类来代表一元运算符节点,而增加了一个新类型的节点后,我们自然还需要添加访问这个新类型节点的方法,因此我们还需要为NodeVisitor编写新接口visitUnaryOp,并为实现类Interpreter添加对应的方法实现。
一元运算符节点类UnaryOp:
public class UnaryOp implements AST {
public Token op;
public AST expr;
public UnaryOp(Token op, AST expr){
this.op = op;
this.expr = expr;
}
}
和二元操作符节点BinOp类非常的类似,不细说。
然后一元运算符应该是属于factor(因数)生成式的一部分,如:-5*3,(-5)整体应该是一个因数
故factor的生成式可修改为:
factor : (PLUS | MINUS) factor | INTEGER | LPAREN expr RPAREN
由此,我们只需为Parser的factor函数添加一种情况即可:
factor函数:
private AST factor() throws Exception {
// factor : (PLUS | MINUS) factor | INTEGER | LPAREN expr RPAREN
Token token = currentToken;
// ++++++这部分是添加的代码
if (token.type == Token.TokenType.PLUS || token.type == Token.TokenType.MINUS){
if (token.type == Token.TokenType.PLUS){
eat(Token.TokenType.PLUS);
}
else {
eat(Token.TokenType.MINUS);
}
return new UnaryOp(token, factor());
}
// ++++++++++++++++++++++
else if (currentToken.type == Token.TokenType.INTEGER){
eat(Token.TokenType.INTEGER);
return new Num(token);
}
else {
eat(Token.TokenType.LPAREN);
AST result = expr();
eat(Token.TokenType.RPAREN);
return result;
}
}
NodeVisitor类:
public abstract class NodeVisitor {
...
abstract int visitUnaryOp(AST node) throws Exception;
}
使用反射的巧妙之处就体现出来了,在这里我们就只需要添加新函数即可,而无需为新类型添加判断之类的新的操作,代码维护起来非常方便。
Interpreter.visitUnaryOp函数:
@Override
int visitUnaryOp(AST node) throws Exception {
UnaryOp unaryOp = (UnaryOp)node;
if (unaryOp.op.type== Token.TokenType.PLUS){
return +visit(unaryOp.expr);
}
else {
return -visit(unaryOp.expr);
}
}
运行效果:

至此,我们已经完成所有的解析四则运算表达式的功能。
上一篇:手写Pascal解释器(二)
下一篇:未完待续


 浙公网安备 33010602011771号
浙公网安备 33010602011771号