手写Pascal解释器(二)
一、part4
承接上次的内容,我们继续编写part4,这个部分我们的任务是完成输入一个仅带乘除运算符的表达式,然后返回表达式的结果。
主要修改或添加的内容:
原来我们的分析工作全部都是放在Interpreter类中完成,但到了现在的阶段,我们将解析的工作放到两个类中进行完成,即原Interpreter类被分解为Lexer和Interpreter类(即Lexer为词法分析器,Interpreter现在为语法分析器):
Lexer类的职责是将字符串根据各个部分的起始字符将其解析成各个Token,如一个空格隔开的子字符串若以数字开头,则解析为TK_Interger,若为“+”开头,则解析为TK_Plus等等。
而Interpreter类则是进行语法分析,如某个结构的表达是:expr : term ((PLUS | MINUS) term)*,则Interpreter类中的某个函数则会调用Lexer类的接口获得每一个Token然后检验结构是否符合预期,并给出总的语法结构的结果。
先看Lexer类:
成员变量和构造函数(将原来Interpreter类中与解析Token相关的变量都移到了Lexer类中):
private final String text;
private int pos;
private Character currentChar;
public Lexer(String text){
this.text = text;
this.pos = 0;
this.currentChar = this.text.charAt(pos);
}
其他解析Token的函数基本都原封不动的搬了过来,只看一下getNextToken()函数:
public Token getNextToken() throws Exception {
while (currentChar != null){
if (isSpace(this.currentChar)){
this.skipWhitespace();
continue;
}
if (Character.isDigit(currentChar)){
return new TK_Integer(this.integer());
}
if (currentChar=='*'){
this.advance();
return new TK_Mul();
}
if (currentChar=='/'){
this.advance();
return new TK_Div();
}
this.error();
}
return new TK_EOF();
}
将对“+”和“-”的解析改为了对“*”和“/”的解析。
Interpreter类:
成员变量和构造函数:
private final Lexer lexer;
private Token currentToken;
public Interpreter(Lexer lexer) throws Exception {
this.lexer = lexer;
this.currentToken = this.lexer.getNextToken();
}
lexer变成了Interpreter类的一个成员,调用它提供的接口来读取Token。
补充理论知识
资料来源:https://ruslanspivak.com/lsbasi-part4/
先来看看我们目标的翻译结构:
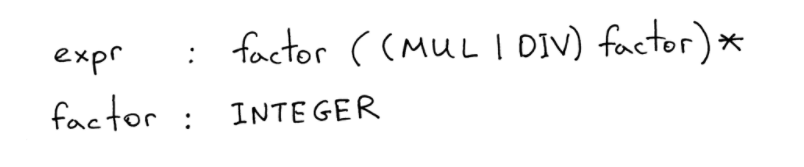
expr翻译成中文应该是初中就学过的数学概念,“多项式”的“项”,而factor翻译为中文应该是“因数”,从上面的结构可以看出,“项”可以是一个“因数”,也可以是多个因数进行若干次相乘除获得;而“因数”是由“整数”构成的
得到结构后如何使用代码进行处理?
链接博客的大佬给了我们一个普遍性的翻译方案:
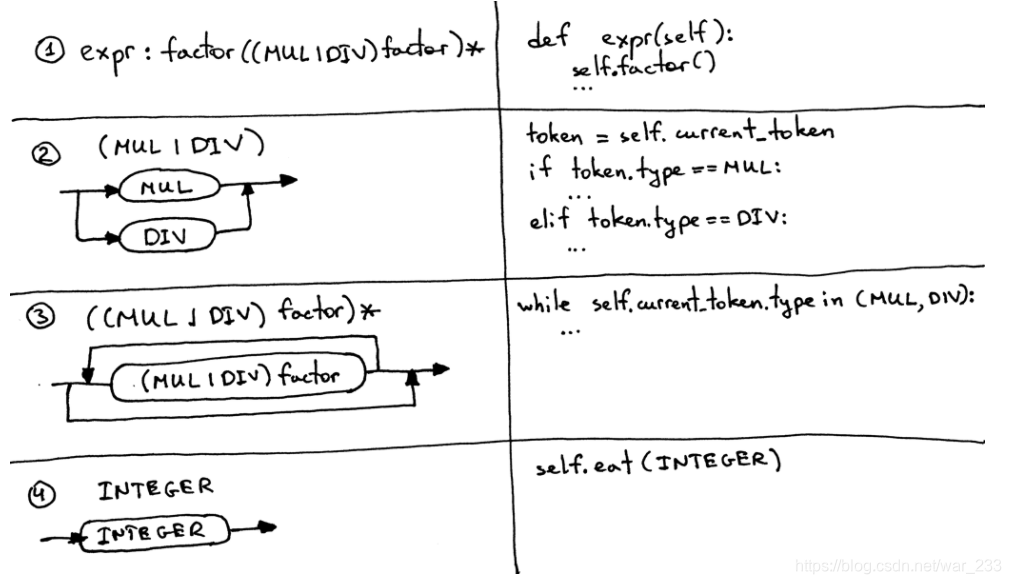
① 每个规则R可以翻译为一个函数
② 替代项(a1 | a2 | aN)成为if-elif-else 语句
③ 可选的分组(…)*成为while语句,可以循环零次或多次
④ 每个Token引用T都成为对eat方法的调用:eat(T)。如果当前的Token与已经写好的Token相匹配,则调用eat,即进行类型判断,然后从词法分析器中获得一个新的Token赋值到current_token成员变量。
这样,我们即可根据写出的生成式和翻译规则对输入的字符串进行相应的处理了。
factor()函数:
private int factor() throws Exception {
// factor : INTEGER
Token token = currentToken;
eat(Token.TokenType.INTEGER);
return (Integer) token.value;
}
expr()函数:
public intexpr() throws Exception {
// term : factor ((MUL | DIV) factor)*
int result = factor();
while (currentToken.type == Token.TokenType.MUL || currentToken.type == Token.TokenType.DIV){
Token token = currentToken;
if (token.type == Token.TokenType.MUL){
eat(Token.TokenType.MUL);
result *= factor();
}
else {
eat(Token.TokenType.DIV);
result /= factor();
}
}
return result;
}
客户端使用:
public class Main {
public static void main(String[] args) throws Exception {
Scanner scanner = new Scanner(System.in);
while (true){
System.out.print("calc> ");
String text = scanner.nextLine();
if (text.equals("exit"))
break;
Lexer lexer = new Lexer(text);
Interpreter interpreter = new Interpreter(lexer);
int res = interpreter.expr();
System.out.println("res: "+res);
}
}
}
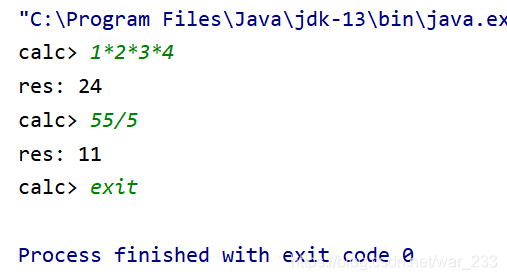
运行结果:
二、part5
part5的任务是在原来支持乘除的基础上加入加减运算。
设计生成式
资料来源:https://ruslanspivak.com/lsbasi-part5/
加入了加减后,表达式的计算就出现了优先级,即“*”、“/”的优先级高于“+”、“-”的优先级。
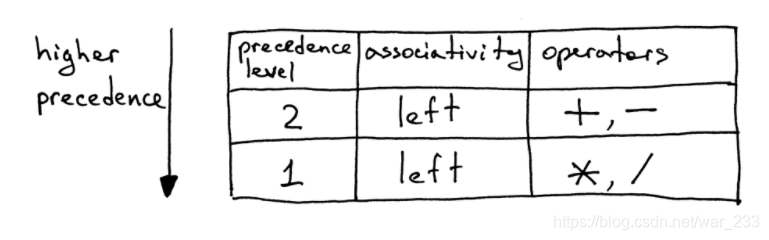
由优先级表如何构造语法规则:

谷歌翻译的结果:(英文太菜😂)
以下是有关如何根据优先级表构造语法的规则:
- 为每个优先级定义一个非终结符。非终端产品的主体应包含该级别的算术运算符和下一个更高优先级的非终端产品。
- 为基本的表达单位(在我们的情况下为整数)创建一个附加的非终止因子。一般规则是,如果您具有N个优先级,则总共将需要N + 1个非末端:每个级别一个非末端,再加上一个基本表达单元的非末端。
大佬给出的生成式:

表达式是一个项,或是一个项进行若干次加减运算得到。乘除运算的优先级是高于加减运算的,故加减运算需要包含下一个更高优先级的非终结符,即通过若干乘除运算得到的term。

项是一个因数,或是一个因数进行若干次乘除运算得到。
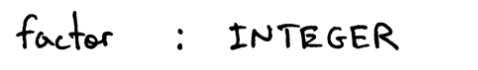
因数是一个整数。
有了生成式和翻译规则,我们就可以轻松写出代码:
expr()函数:
public int expr() throws Exception {
/*
expr : term ((PLUS | MINUS) term)*
term : factor ((MUL | DIV) factor)*
factor : INTEGER
*/
int result = term();
while (currentToken.type == Token.TokenType.PLUS || currentToken.type == Token.TokenType.MINUS){
Token token = currentToken;
if (token.type == Token.TokenType.PLUS){
eat(Token.TokenType.PLUS);
result += term();
}
else {
eat(Token.TokenType.MINUS);
result -= term();
}
}
return result;
}
term()函数:
private int term() throws Exception {
// term : factor ((MUL | DIV) factor)*
int result = factor();
while (currentToken.type == Token.TokenType.MUL || currentToken.type == Token.TokenType.DIV){
Token token = currentToken;
if (token.type == Token.TokenType.MUL){
eat(Token.TokenType.MUL);
result *= factor();
}
else {
eat(Token.TokenType.DIV);
result /= factor();
}
}
return result;
}
factor()函数:
private int factor() throws Exception {
// factor : INTEGER
Token token = currentToken;
eat(Token.TokenType.INTEGER);
return (Integer) token.value;
}
运行结果:

三、part6
资料来源:https://ruslanspivak.com/lsbasi-part6/
part6的任务是在前面的基础上添加括号(即“(”和“)”)的支持。
更新后的生成式:
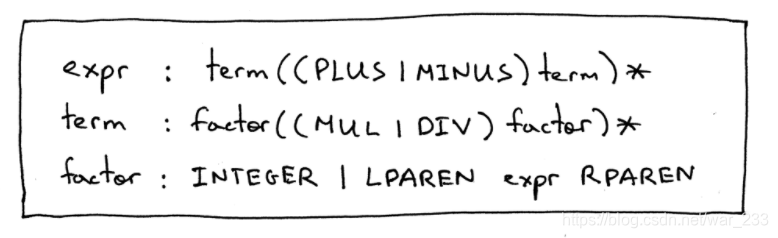
从图中也可以看出,因数除了是一个整数,也可以是由左右括号包含的表达式,而且由前面的根据优先级编写生成式的方法也可以知道,左右括号的优先级是比带有乘除运算的expr的优先级要更高的。
由生成式,我们只需要添加两个Token:TK_Lparen和TK_Rparen,以及修改factor()函数实现即可。
添加Token较为简单,这里不再赘述。
更新后的factor():
private int factor() throws Exception {
// factor : INTEGER | LPAREN expr RPAREN
Token token = currentToken;
if (currentToken.type == Token.TokenType.INTEGER){
eat(Token.TokenType.INTEGER);
return (Integer) token.value;
}
else {
eat(Token.TokenType.LPAREN);
int result = expr();
eat(Token.TokenType.RPAREN);
return result;
}
}
运行结果:

至此,我们完成了part6的内容,现在我们的表达式解析器已经可以解析几乎大部分的加减乘除表达式了!
上一篇:手写Pascal解释器(一)
下一篇:手写Pascal解释器(三)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号