Prüfer 序列
Prüfer 序列
Prüfer 序列是将一颗 \(n\) 个有标号的点用一个长度为 \(n-2\) 的序列的表示的方法。
对于一颗有标号的树，会存在唯一一个 Prüfer 序列与之对应。一个 Prüfer 序列也只会对应一颗树。
将一颗树转化为 Prüfer 序列
首先对于所有的叶子节点（此时为 \(1,2,4,6\)），选择其编号最小的节点删掉。然后将其父亲节点加入 Prüfer 序列中。
在重复经过 \(n-2\) 次操作后，剩余了 \(2\) 个点，构造结束。
过程
对于一颗有标号的树：
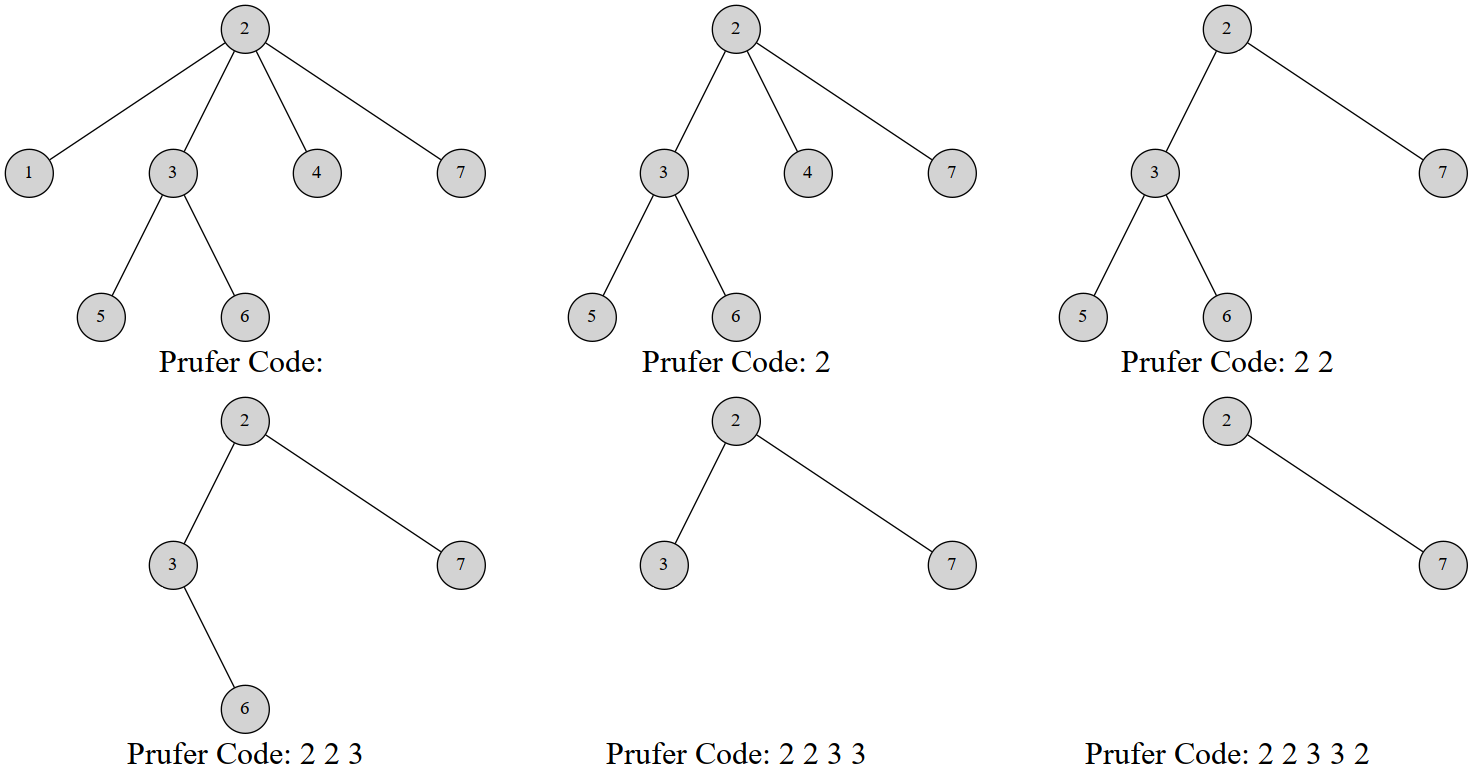
显而易见地是，1. 可以用一个小根堆来维护所有的叶子节点。
-
每次取出堆中最小的元素删除。
-
在每次删除节点后，判断它的父亲节点是否成为叶子节点，如果是，加入堆中。
-
重复操作，直至还剩 \(2\) 个节点。
for(int i=1;i<n;i++) {
cin>>u>>v;
addedge(u,v); addedge(v,u);
d[u]++; d[v]++;
}
for(int i=1;i<=n;i++) {
if(d[i]==1) q.push(i);
}
for(int i=1;i<=n-2;i++) {
int u=q.top(), v; q.pop();
vis[u]=true;
for(int k=hd[u];i;i=nxt[i]) {
if(!vis[to[i]]) v=to[i];
}
if(--d[v]==1) q.push(v);
}
for(int i=1;i<=n-2;i++) cout<<p[i]<<' ';
这样的做法的时间复杂度是 \(\text O(n\log_2n)\) 的。
线性做法 & 过程
通过维护一个指针 \(p\)，初始时 \(p\) 指向编号最小的叶子节点，然后
- 将 \(p\) 指向的节点删掉。判断与这个节点相连的节点是否成为叶子节点。
- 如果是，判断该节点的编号 \(x\) 是否大于 \(p\) 所指向的节点编号。如果大于，不做操作，否则，将节点 \(x\) 删掉，并判断与这个节点相连的节点是否成为叶子节点。重复操作 \(2\) 直至无法操作。
- 将指针 \(p\) 自增，直至到一个未被删掉的节点。
性质
可以发现，在 Prüfer 序列中，每个点 \(u\) 的出现次数是其点的度数 \(d_u-1\) 。
-
对于叶子节点，一定不会存在 Prufer序列中。
-
对于非叶子节点 \(u\)，在节点 \(u\) 被删掉前，会有与之相连的 \(d_u-1\) 的节点会被删掉（其原因是在构造 Prufer序列的过程中树是联通的，且树大小始终不小于 \(2\)），在这个过程中，节点 \(u\) 就会被加入 Prufer序列 \(d_u-1\) 次。
由此也可以知道 \(\sum_{i=1}^{n}(d_u-1)=n-2\)。
- 剩下的 \(2\) 个节点中，其中一个是编号最大的节点，且它绝对不会计入叶子节点中。
Prüfer 序列将转化为一颗树
过程
考虑将上述转化的过程，重复一遍。
-
对于 Prüfer 序列的第一个数 \(u\) ，和它相连的节点 \(v\) 一定是叶子节点中编号最小的。将 \(u\) 与 \(v\) 连边。
-
那么维护一个叶子节点集合 \(S\)，将这个编号最小的节点 \(v\) 删掉。
-
此时将 Prüfer 序列的第一个数也删掉，由于叶子节点在 Prüfer 序列的出现次数为 \(d-1=0\)，那么如果这个数在 Prüfer 序列中的出现次数变为 \(0\) 的话，节点 \(u\) 变为叶子节点，加入集合 \(S\) 中。
-
重复该过程 \(n-2\) 次。
-
最终在集合 \(S\) 中会存在 \(1\) 个节点，将其和最大节点连接即可。
for(int i=1;i<=n-2;i++) {
cin>>p[i]; d[p[i]]++;
}
for(int i=1;i<=n;i++) {
if(!d[i]) q.push(i);
}
for(int i=1;i<=n-2;i++) {
int u=q.top(); q.pop();
addedge(p[i],u); addedge(u,p[i]);
if(--d[p[i]]==0) q.push(p[i]);
}
addedge(n,q.top()); addedge(q.top(),n);
这个过程也可以使用堆维护，当然也存在线性做法。
线性做法 & 过程
同样是维护一个指针指向叶子节点中的编号最小的节点。
性质
- 无向完全图的不同生成树数（Cayley公式）
对于一个 \(n\) 个点的无向完全图，任意一个长度为 \(n-2\) 的 Prüfer 序列都可以构造出一个不同的具有 \(n\) 个点的树。
所以讲，会有 \(n^{n-2}\) 个不同的 Prüfer 序列构成 \(n\) 个点的树，那么无向完全图的不同生成树数也就是 \(n^{n-2}\) 个。
- \(n\) 个点无根树计数，且已知每个点的点度。
由于每个点在 Prüfer 序列中的出现次数为 \(d_i-1\)，所以可以利用组合知识求出。
展开可以得到
