知识杂项(知识堆砌)
也就是杂杂的记一下
1. 大数翻倍法
用于解决线性同余方程组(中国剩余定理)的一种优化暴力,好写好记,而且正确率较高。
暴力做法:对于其中两个同余方程进行合并
wihle (a1%n2!=a2) a1+=n1;
return (a1, lcm(n1,n2));
复杂度好像是一种 \(\sum n_i-\max n_i\) (\(n_i\) 为模数) 的奇怪的东西。
具体做法是将暴力的做法优化了些。
inline node merge(node a, node b)
{
if (a.m < b.m) swap(a, b);
//唯一的优化
while (a.a%b.m != b.a)
a.a += a.m;
a.m = lcm(a.m, b.m);
return a;
}
后话:洛谷的CRT模板题,虽然暴力也能水过。但这三者之间的速度差异依然可以由P4777 【模板】扩展中国剩余定理(EXCRT)看出。

2. 图中的一些定义(备忘)
最大匹配数:最大匹配的匹配边的数目
最小点覆盖数:选取最少的点,使任意一条边至少有一个端点被选择
最大独立集:选取最多的点,使任意所选两点均不相连
最小路径覆盖数:对于一个 \(\small\text {DAG}\)(有向无环图),选取最少条路径,使得每个顶点属于且仅属于一条路径。路径长可以为 \(0\)(即单个点)。
团:选出一些顶点,这些顶点两两之间都有边。最大团就是使得选出的这个顶点集合最大。
关于二分图一些定理:
-
最大匹配数 = 最小点覆盖数(König 定理) -
最大独立集 = 点数 - 最大匹配数 -
最小路径覆盖数 = 点数 - 最大匹配数 -
(二分图的补图的)最大团的大小 = 其补图最大独立集的大小
3. 哈希值
4. 同余最短路
看似这种 “随意使用 \(n\) 个,可以拼凑(相加)出的数的个数” 或是 “无法拼凑出的最小(最大)的数” 等等,和图论完全不着边际的问题,可以用同余最短路试试看。
最短路有一个 \(dis\) 数组存储最短路长度的数组,然后同余最短路的 \(dis\) 数组的效用是:
设 \(x\) 为一个被拼凑出来的数,那么 \(dis_{i}\) 是 \(x\) 模 \(p\) 余 \(i\) 的最小被拼凑出来的数。
\(p\) 是给出的 \(n\) 个数中的任意一个数,通常它会是 \(a_{min}\),\(p\) 的选择就代表着这图的点数,所以说小凯的疑惑这种题就算了吧。
然后就有了 \(u\xrightarrow{a_i} u+a_i \bmod p\) 这样的建图方法,边跑边建。
有了 \(dis_i\) 这样的数组,上述问题就有了方法,
-
可以拼凑(相加)出的数 \(x\in[l, r]\) 的个数:\(\sum_{i=0}^{p}\frac{(r-dis_i)}{p}+1, \ \ dis_i<=r\)。
-
无法(可以)拼凑出的最小(最大)的数,很明显 \(dis_i\) 是可以,\(dis_i-p\) 是不可以。
如果解决可以拼凑出的 \(k-th\) 的数,建议看看某一场 AT 的 E 。
5. 线段树优化建图
由于某些奇奇怪怪的题目要求由一个区间里的点连向其他的点,这样的建边极为的繁琐。
我们可以建一个虚点来表示这个区间的点,就像是这样。

但此时,这个虚点又并不和 \([l,r]\) 的点所联系,那么就可以这样。
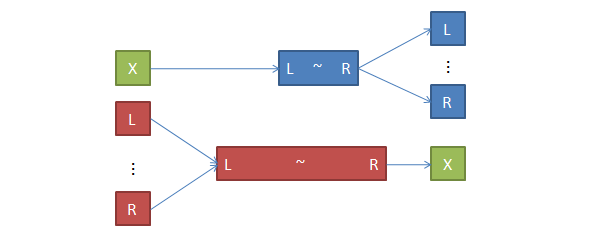
由于这样还是太繁琐了,聪明的人们想到了线段树,就像是这样。(当然你完全可以把两颗线段树的叶子节点建出来,直接的把两个线段树分开,再在叶子节点对应连边)
之后就可以在这颗线段树上进行建边了。
特别提醒:线段树 \(1\) 是一颗代表终点节点区间的树,而线段树 \(2\) 是一颗代表起点节点区间的树。
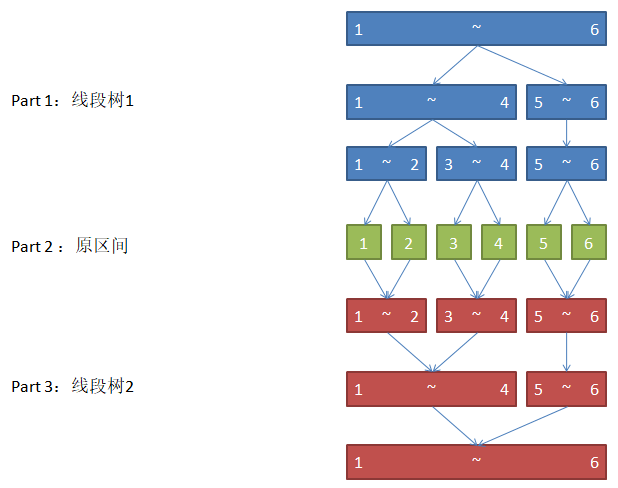
偶尔的区间连区间的问题,让它变为区间连虚点连区间即可。
6. 哥德巴赫猜想
哥德巴赫猜想的现代版本是:
每个大于2的偶数都可以写成两个素数之和。
这里有一个小结论:分成的两个质数中,有一个小质数一定小于 \(n\)。



