2.2 节的练习--Compiler principles, technologys, &tools
2.2 节的练习
2.2.1
考虑下面的上下文无关文法:
S -> S S + | S S * | a
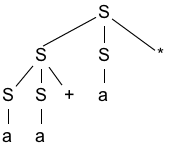
- 试说明如何使用该文法生成串 aa+a*
- 试为这个串构造一颗语法分析树
- ⧗ 该文法生成的语言是什么?试证明
解答
2.2.2
下面各个文法生成什么语言?证明你的每一个答案
- S -> 0 S 1 | 0 1
- S -> + S S | - S S | a
- S -> S ( S ) S | ε
- S -> a S b S | b S a S | ε
- ⧗ S -> a | S + S | S S | S * | ( S )
解答
- L = {0n1n | n>=1}
- L = {支持加法和减法的表达式的前缀表达形式}
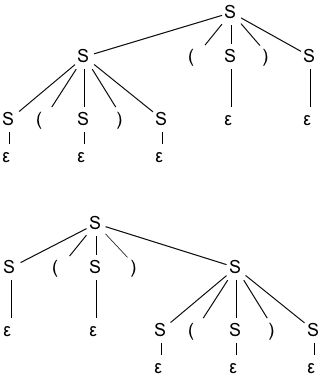
- L = {匹配括号的任意排列和嵌套的括号串,包括 ε}
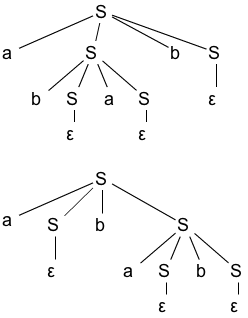
- L = {数量相同的a和b组成的符号串,包括 ε}
- ?
2.2.3
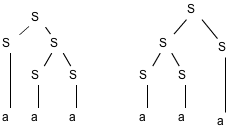
上一题中哪些文法具有二义性
解答
为下面的各个语言构建无二义性的上下文无关文法。证明你的文法都是正确的。
- 用后缀方法表示的算数表达式
- 由逗号分隔开的左结合的标识符列表(标识符以 id 表示,以下同)
- 由逗号分隔开的右结合的标识符列表
- 有整数、标识符、4个二目运算符 +, -, *, / 构成的算数表达式
- ! 在上一题的运算符中增加单目+ 和单目-构成的算数表达式
解答
- E -> E E op | num
- list -> list , id | id
- list -> id , list | id
-
expr -> expr + term | expr - term | term
term -> term * factor | term / factor | factor
factor -> id | num | (expr)
-
注:单目加减运算的优先级最高
expr -> expr + term | expr - term | term
term -> term * unary | term / unary | unary
unary -> + factor | - factor
factor - > id | num | (expr)
2.2.5
-
证明:用下面文法生成的所有二进制串的值都能被3整除。(提示:对语法分析树的节点树木使用数学归纳法)
num -> 11 | 1001 | num 0 | num num
-
上面的文法是否能生成所有能被3整除的二进制串?
解答
-
证明
符合该文法的二进制串一定是由任意数量的 11,1001 和 0 组成的最左位不为0的序列
该序列的十进制和为:
sum
= Σn (21 + 20) * 2 n + Σm (23 + 20) * 2m
= Σn 3 * 2 n + Σm 9 * 2m
显然是能被3整除的
-
不是。二进制串10101,数值为21,可被3整除,但无法由文法推导出。
注: 还有更一般性的证法么?
2.2.6
为罗马数字构建一个上下文无关文法
注:该文法不考虑罗马数字的上下划线表示,故只能产生小于4k的数字
解答
规则参考 维基百科:罗马数字
-
根据wiki中讲述的规则,可以发现个位数的表示可以分为4类:
I, II, III | I V | V, V I, V II, V III | I X
即有产生式:
digit -> smallDigit | I V | V smallDigit | I X
smallDigit -> I | II | III | ε
其他数位的表示类似。
-
还可以发现:罗马数字和阿拉伯数字有比较简单的数位对应关系。
例如:
- XII - X, II - 10 + 2 - 12
- CXCIX - C, XC, IX - 100 + 90 + 9 - 199
- MDCCCLXXX - M, DCCC, LXXX - 1000 + 800 + 80 - 1880
-
根据这两个规律推导出产生式:
romanNum -> thousand hundred ten digit
thousand -> M | MM | MMM | ε
hundred -> smallHundred | C D | D smallHundred | C M
smallHundred -> C | CC | CCC | ε
ten -> smallTen | X L | L smallTen | X C
smallTen -> X | XX | XXX | ε
digit -> smallDigit | I V | V smallDigit | I X
smallDigit -> I | II | III | ε
posted on 2014-03-06 16:27 compilerTech 阅读(1861) 评论(0) 收藏 举报



 浙公网安备 33010602011771号
浙公网安备 33010602011771号