20180702小测

这场考试我其实并没有参加......
因为一些奥妙重重的原因肚子疼到厌生，没看完题就滚回家了......
马上就NOI了还是这种身体状态，真是要完。

T1:

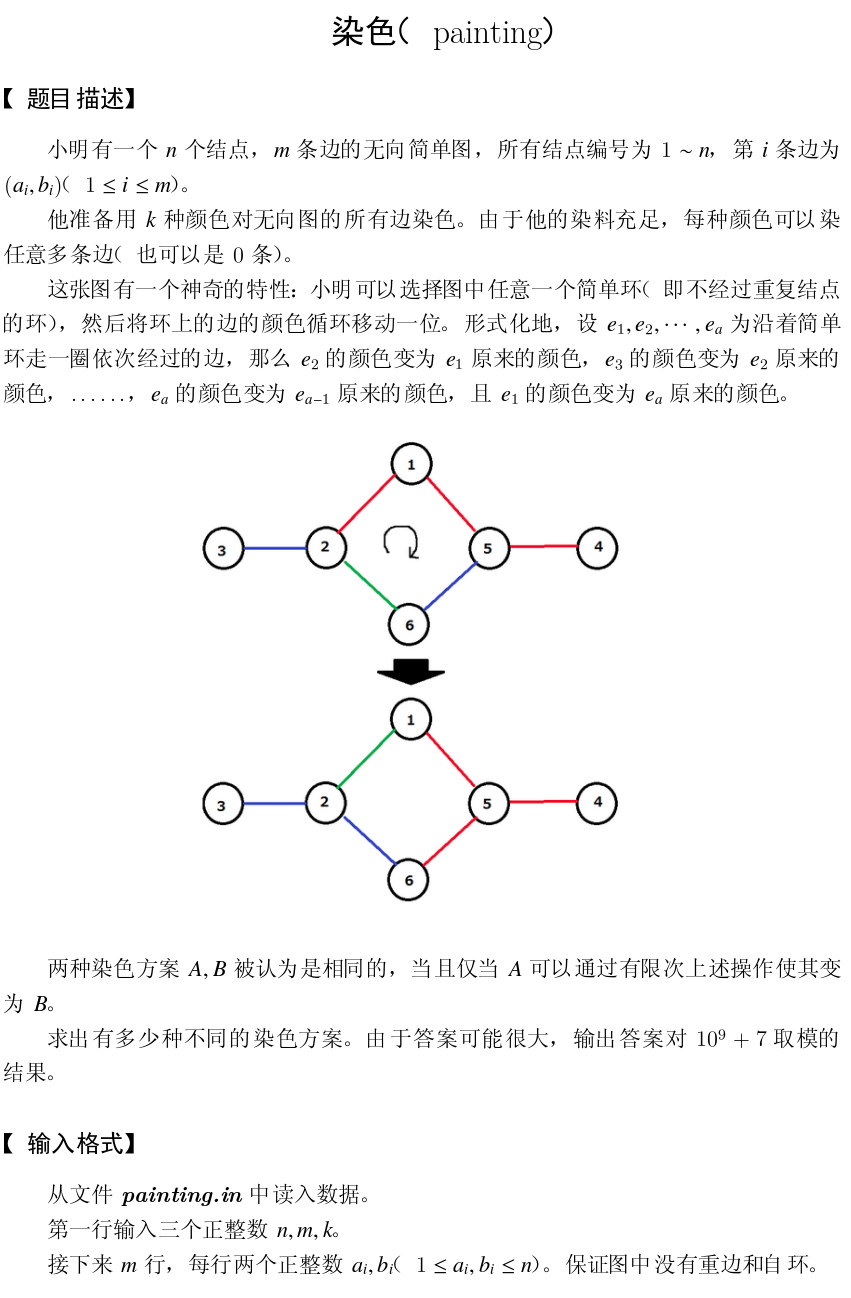
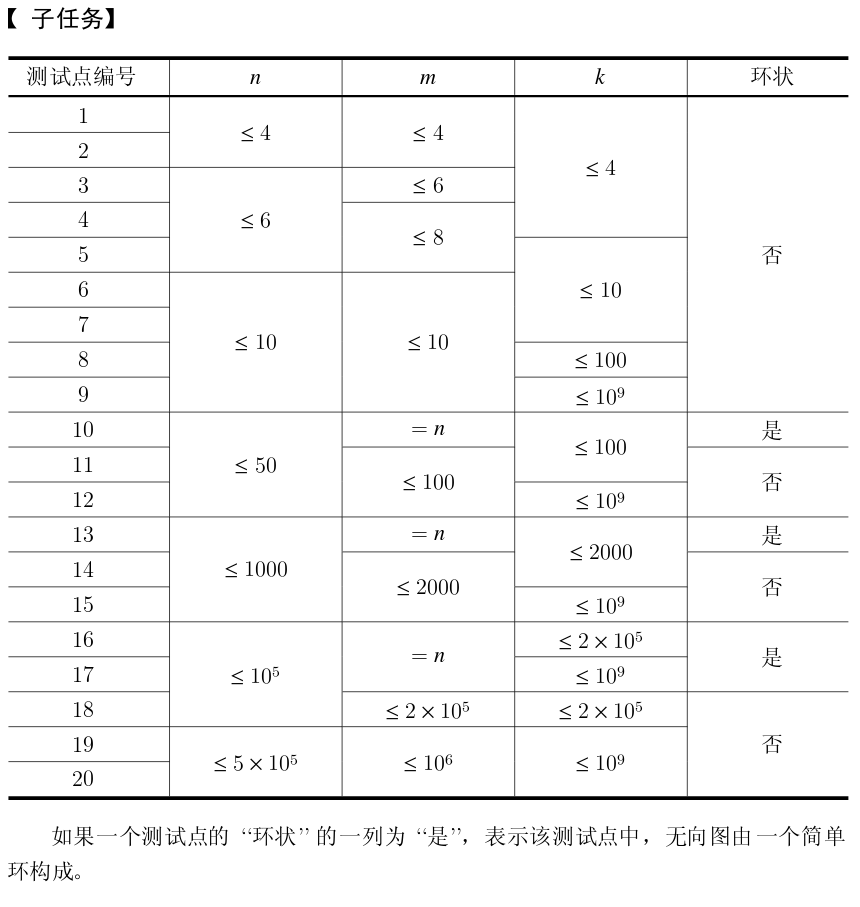
我们先把所有点双联通分量缩起来。
如果这个双联通分量只有一条边，那么方案数显然是k；
如果这个双联通分量恰好是一个环，那么方案数可以用polya定理计算；
否则，这个双联通分量的任意两条边可以互换颜色(自行构造一下就知道了)，所以方案数只和某种颜色出现几次有关，大力插板即可。
双联通分量的形态怎么判？记录点数和边数判断即可。
具体就是用vector存下来每个分量的每条边，然后暴力数点即可。
(这里吐槽一句求点双联通分量栈里面压点的都是邪教！你那么做根本没法统计返祖边！)
代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#include<cctype>
#define debug cout
typedef long long int lli;
using namespace std;
const int maxn=5e5+1e2,maxe=1e6+1e2;
const int mod=1e9+7;

int inv[maxe];
inline int mul(const int &x,const int &y) {
    return (lli) x * y % mod;
}
inline void adde(int &dst,const int &x) {
    if( ( dst += x ) >= mod ) dst -= mod;
}
inline void mule(int &dst,const int &x) {
    dst = (lli) dst * x % mod;
}
inline int fastpow(int base,int tim) {
    int ret = 1;
    while(tim) {
        if( tim & 1 ) mule(ret,base);
        if( tim >>= 1 ) mule(base,base);
    }
    return ret;
}
inline int c(int x,int y) {
    int ret = 1;
    for(int i=0;i<y;i++) mule(ret,x-i);
    for(int i=1;i<=y;i++) mule(ret,inv[i]);
    return ret;
}
inline int gcd(int x,int y) {
    register int t;
    while( t = x % y ) x = y , y = t;
    return y;
}

int u[maxe],v[maxe];
int s[maxn],t[maxe<<1],nxt[maxe<<1];
int dfn[maxn],low[maxn],stk[maxe],top,fs;
vector<int> es[maxn<<1];
bool vis[maxn];
int n,m,k,ans=1;

inline void coredge(int from,int to) {
    static int cnt = 1;
    t[++cnt] = to , nxt[cnt] = s[from] , s[from] = cnt;
}
inline void addedge(int a,int b) {
    coredge(a,b) , coredge(b,a);
}
inline void dfs(int pos,int sou) {
    static int dd; low[pos] = dfn[pos] = ++dd , vis[pos] = 1;
    for(int at=s[pos];at;at=nxt[at]) if( at != ( sou ^ 1 ) ) {
        if( !vis[t[at]] ) {
            stk[++top] = at;
            dfs(t[at],at) , low[pos] = min( low[pos] , low[t[at]] );
            if( low[t[at]] >= dfn[pos] ) {
                int x; ++fs;
                do es[fs].push_back((x=stk[top--])>>1); while( x != at );
            }
        } else {
            if( dfn[t[at]] < dfn[pos] ) stk[++top] = at;
            low[pos] = min( low[pos] , dfn[t[at]] );
        }
    }
}
inline void calc_ring(const vector<int> &vec) {
    if( vec.size() == 1 ) return mule(ans,k);
    int ps = 0;
    for(unsigned i=0;i<vec.size();i++) {
        if( !vis[u[vec[i]]] ) ps += vis[u[vec[i]]] = 1;
        if( !vis[v[vec[i]]] ) ps += vis[v[vec[i]]] = 1;
    }
    for(unsigned i=0;i<vec.size();i++) vis[u[vec[i]]] = vis[v[vec[i]]] = 0;
    if( ps == (signed)vec.size() ) {
        int ret = 0;
        for(int i=1;i<=ps;i++) adde(ret,fastpow(k,gcd(i,ps)));
        mule(ret,inv[ps]) , mule(ans,ret);
    } else mule(ans,c(k+vec.size()-1,vec.size()));
}

inline void init() {
    inv[0] = inv[1] = 1;
    for(int i=2;i<=m;i++) inv[i] = mul(mod-mod/i,inv[mod%i]);
}

inline int getint() {
    int ret = 0 , ch;
    while( !isdigit(ch=getchar()) );
    do ret = ret * 10 + ch - '0'; while( isdigit(ch=getchar()) );
    return ret;
}

int main() {
    n = getint() , m = getint() , k = getint() , init();
    for(int i=1;i<=m;i++) addedge(u[i]=getint(),v[i]=getint());
    for(int i=1;i<=n;i++) if( !vis[i] ) dfs(i,0);
    memset(vis,0,sizeof(vis));
    for(int i=1;i<=fs;i++) calc_ring(es[i]);
    printf("%d\n",ans);
    return 0;
}

T2:

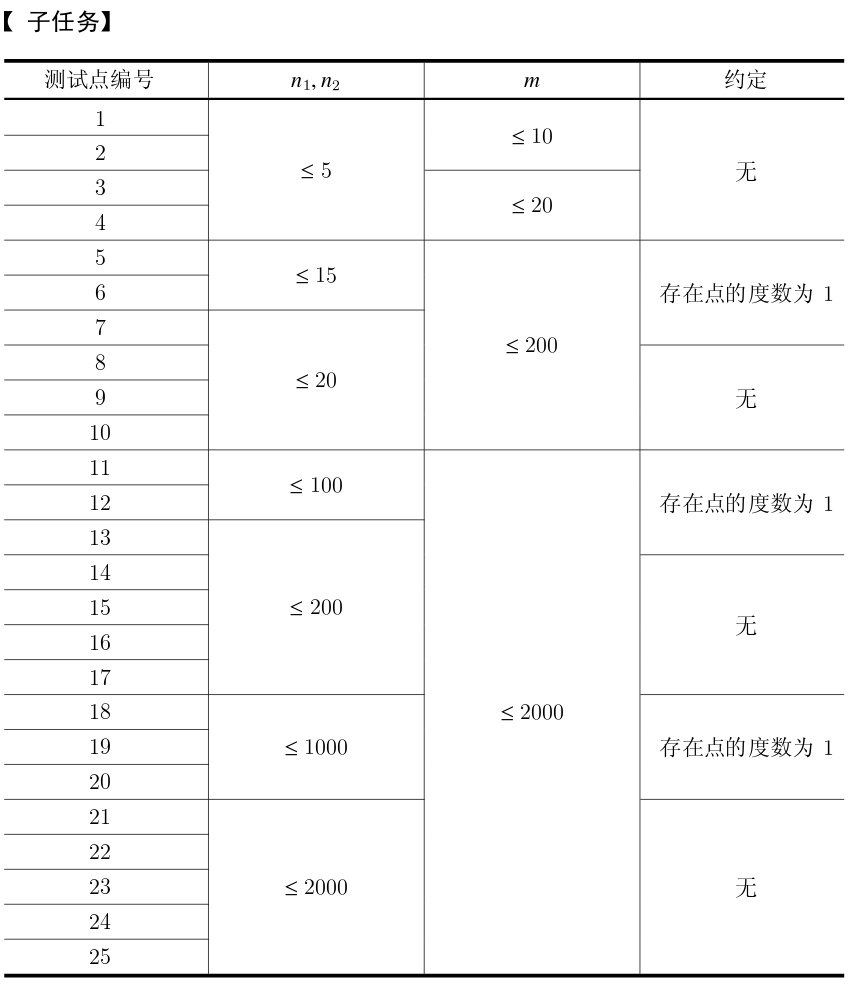
我会有下界的最小流！
等等，为什么要按照上下界建图呢？直接从钦定边全选的状态开始退流就行了，限制每个点能退的流量。水题！
然而SPJ还得自己改......
代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cctype>
#define debug cout
using namespace std;
const int maxn=4e3+1e2,maxe=8e3+1e2;
const int inf=0x3f3f3f3f;

int u[maxn],v[maxn],deg[maxn];
int n1,n2,m,mi=inf;

namespace NetworkFlow {
    int s[maxn],t[maxe],nxt[maxe],f[maxe],cnt;
    int dep[maxn],st,ed;
    inline void coredge(int from,int to,int flow) {
        t[++cnt] = to , f[cnt] = flow , nxt[cnt] = s[from] , s[from] = cnt;
    }
    inline void singledge(int from,int to,int flow) {
        coredge(from,to,flow) , coredge(to,from,0);
    }
    inline bool bfs() {
        memset(dep,-1,sizeof(dep)) , dep[st] = 0;
        queue<int> q; q.push(st);
        while( q.size() ) {
            const int pos = q.front(); q.pop();
            for(int at=s[pos];at;at=nxt[at]) if( f[at] && !~dep[t[at]] ) {
                dep[t[at]] = dep[pos] + 1 , q.push(t[at]);
            }
        }
        return ~dep[ed];
    }
    inline int dfs(int pos,int flow) {
        if( pos == ed ) return flow;
        int ret = 0 , now = 0;
        for(int at=s[pos];at;at=nxt[at]) if( f[at] && dep[t[at]] > dep[pos] ) {
            now = dfs(t[at],min(flow,f[at])) , ret += now , flow -= now , f[at] -= now , f[at^1] +=  now;
            if( !flow ) return ret;
        }
        if( !ret ) dep[pos] = -1;
        return ret;
    }
    inline int dinic() {
        int ret = 0;
        while( bfs() ) ret += dfs(st,inf);
        return ret;
    }
    inline void reset() {
        memset(s,0,sizeof(s)) , cnt = 1;
    }
}

inline void build(int k) {
    NetworkFlow::reset() , NetworkFlow::st = n1 + n2 + 1 , NetworkFlow::ed = n1 + n2 + 2;
    for(int i=1;i<=m;i++) NetworkFlow::singledge(n1+v[i],u[i],1);
    for(int i=1;i<=n1;i++) NetworkFlow::singledge(i,NetworkFlow::ed,deg[i]-k);
    for(int i=n1+1;i<=n1+n2;i++) NetworkFlow::singledge(NetworkFlow::st,i,deg[i]-k);
}
inline void printans() {
    static int seq[maxn],sql; sql = 0;
    using namespace NetworkFlow; dinic();
    for(int i=1;i<=m;i++) if( f[i<<1] ) seq[++sql] = i;
    sort(seq+1,seq+1+sql) , printf("%d ",sql);
    for(int i=1;i<=sql;i++) printf("%d ",seq[i]);
    putchar('\n');
}

inline int getint() {
    int ret = 0 , ch;
    while( !isdigit(ch=getchar()) );
    do ret = ret * 10 + ch - '0'; while( isdigit(ch=getchar()) );
    return ret;
}

int main() {
    n1 = getint() , n2 = getint() , m = getint();
    for(int i=1;i<=m;i++) ++deg[u[i]=getint()] , ++deg[n1+(v[i]=getint())];
    for(int i=1;i<=n1+n2;i++) mi = min( mi , deg[i] );
    for(int i=0;i<=mi;i++) build(i) , printans();
    return 0;
}

SPJ:

#include<cstdio>
#define WA return puts("0"),0
#define AC return puts("4"),0
int n1,n2,m,u[2010],v[2010],md,ans[2010],deg[2][2010];
bool used[2010];
int full;
int main(int argc,char*argv[]){
    freopen(argv[1],"r",stdin);
    scanf("%d%d%d",&n1,&n2,&m);
    for(int i=0;i<m;i++)scanf("%d%d",u+i,v+i);
    freopen(argv[3],"r",stdin);
    md=-1;
    while(scanf("%d",ans+(++md))==1){
        for(int i=ans[md];i--;)scanf("%*d");
    }
    md--;
    freopen(argv[2],"r",stdin);
    freopen(argv[5],"w",stdout);
    for(int i=0;i<=md;i++){
        int c;
        if(scanf("%d",&c)!=1||c!=ans[i])WA;
        for(int j=0;j<m;j++)used[j]=0;
        for(int j=0;j<n1;j++)deg[0][j]=0;
        for(int j=0;j<n2;j++)deg[1][j]=0;
        while(c--){
            int x;
            if(scanf("%d",&x)!=1||x<1||x>m||used[x-1])WA;
            used[--x]=1;
            deg[0][u[x]]++;
            deg[1][v[x]]++;
        }
        for(int j=1;j<=n1;j++)if(deg[0][j]<i)WA;
        for(int j=1;j<=n2;j++)if(deg[1][j]<i)WA;
    }
    AC;
}

 

T3:

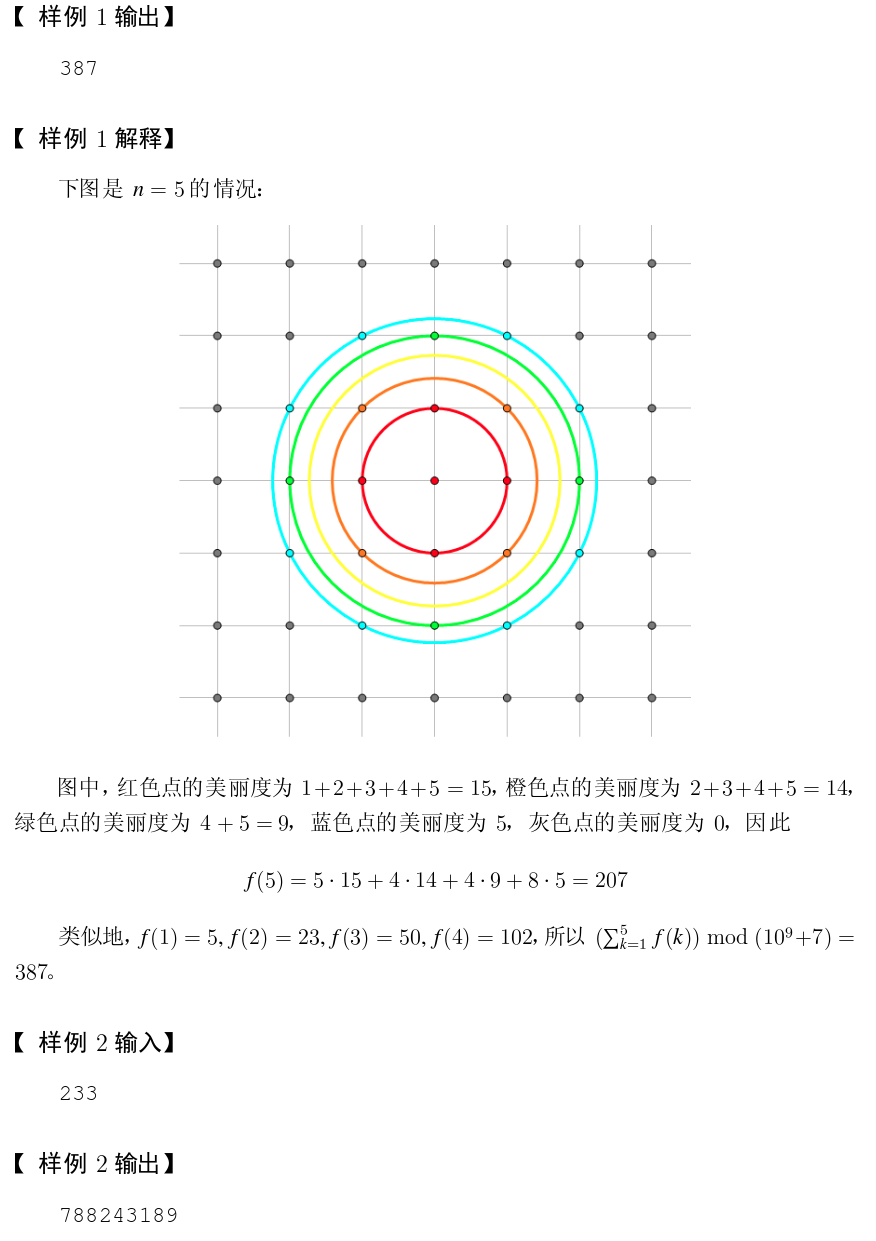
一脸不可做的样子......
考虑对每个点统计覆盖它的圆的贡献。
我们先计算第一象限(含x轴)的答案，最后乘4在加上原点的贡献即可。
考虑枚举点的坐标，我们有: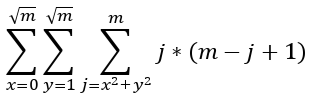

(后面j是在枚举能覆盖这个点的圆，后面乘的是这个圆被统计的次数)
我们令: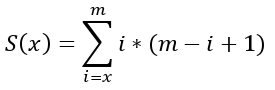

显然关于x的k次多项式的前缀和或有上界的后缀和都是一个关于x的k+1次多项式。所以这个s我们能拉格朗日插值。
那么我们的公式能化为: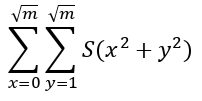

我们令: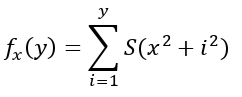

就是一个把x当做常数，关于y的函数了。
我们理性分析一下，S(x)是关于x的3次多项式，那么S(x^2+y^2)就是关于y的6次多项式，而这个东西是S(x^2+y^2)的前缀和，就是关于y的7次多项式喽。
于是我们又能大力拉格朗日插值......
然后我们枚举x，这题就做完了......复杂度O(sqrt(m))，常数巨大，最后一个点要7s......
代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define debug cout
typedef long long int lli;
using namespace std;
const int mod=1e9+7;

inline int add(const int &x,const int &y) {
    const int ret = x + y;
    return ret >= mod ? ret - mod : ret;
}
inline int sub(const int &x,const int &y) {
    const int ret = x - y;
    return ret < 0 ? ret + mod : ret;
}
inline int mul(const int &x,const int &y) {
    return (lli) x * y % mod;
}
inline void adde(int &dst,const int &x) {
    if( ( dst += x ) >= mod ) dst -= mod;
}
inline void sube(int &dst,const int &x) {
    if( ( dst -= x ) < 0 ) dst += mod;
}
inline void mule(int &dst,const int &x) {
    dst = (lli) dst * x % mod;
}
inline int fastpow(int base,int tim) {
    int ret = 1;
    while(tim) {
        if( tim & 1 ) mule(ret,base);
        if( tim >>= 1 ) mule(base,base);
    }
    return ret;
}

struct Interval {
    int xs[11],ys[11],ps[11],cnt;
    inline void insert(const int &x,const int &y) {
        xs[++cnt] = x , ys[cnt] = y;
    }
    inline void init() {
        for(int i=1;i<=cnt;i++) {
            ps[i] = 1;
            for(int j=1;j<=cnt;j++) if( j != i ) mule(ps[i],sub(xs[i],xs[j]));
            ps[i] = fastpow(ps[i],mod-2);
        }
    }
    inline int calc(const int &x) {
        int ret = 0;
        for(int i=1;i<=cnt;i++) {
            int pi = 1;
            for(int j=1;j<=cnt;j++) if( j != i ) mule(pi,sub(x,xs[j]));
            adde(ret,mul(mul(pi,ps[i]),ys[i]));
        }
        return ret;
    }
    inline void reset() {
        cnt = 0;
    }
}s,f;

lli m;
int sq,ans;

inline void inits() {
    const int m = ::m % mod;
    for(int i=m,su;i>m-4;i--) {
        su = 0;
        for(int j=i;j<=m;j++) adde(su,mul(j,sub((m+1)%mod,j)));
        s.insert(i,su);
    }
    s.init();
}
inline void initf(int x) {
    f.reset();
    for(int i=1,su=0;i<=8;i++) adde(su,s.calc(((lli)x*x+i*i)%mod)) , f.insert(i,su);
    f.init();
}

int main() {
    scanf("%lld",&m) , inits() , sq = sqrt(m);
    for(int i=0;i<=sq;i++) {
        if( (lli) i * i + 8 * 8 <= m ) initf(i) , adde(ans,f.calc((lli)sqrt(m-(lli)i*i)%mod));
        else {
            int t = sqrt(m-(lli)i*i);
            for(int j=1;j<=t;j++) adde(ans,s.calc(((lli)i*i+j*j)%mod));
        }
    }
    mule(ans,4) , adde(ans,s.calc(0)) , printf("%d\n",ans);
    return 0;
}

夜(よる)が明(あ)けて朝(あさ)が来(く)る
黑夜终去 黎明终来
星空(ほしぞら)が朝(あさ)に溶(と)けても
繁星即使融化于晨
君(きみ)の辉(かがや)きはわかるよ
我依可见君之光辉
思(おも)い出(で)を羽(は)ばたかせ
思念化为羽翼
君(きみ)の空(そら)へ舞(ま)い上(あ)がる
飞向星之所在