20180620小测
为什么这么多原题......
T1:

这题我做过,「BZOJ2568: 比特集合」了解一下,此题终结。
代码:

1 #pragma GCC optimize("Ofast") 2 #include<cstdio> 3 #include<algorithm> 4 #include<tr1/unordered_set> 5 #include<cctype> 6 typedef long long int lli; 7 using namespace std; 8 using namespace tr1; 9 const int maxk=18; 10 const lli lim=(1<<18)+5; 11 12 struct BinaryIndexTree { 13 int dat[lim]; 14 #define lowbit(x) (x&-x) 15 inline void update(int pos,const int &x) { 16 while( pos < lim ) dat[pos] += x , pos += lowbit(pos); 17 } 18 inline int query(int pos) { 19 int ret = 0; 20 while(pos) ret += dat[pos] , pos -= lowbit(pos); 21 return ret; 22 } 23 }bit[maxk]; 24 25 lli sum; 26 unordered_multiset<lli> app; 27 28 inline void update(lli x,const int &t) { 29 for(int i=0;i<maxk;i++) bit[i].update( ( x & ((1<<(i+1))-1) ) + 1 , t ); 30 } 31 inline int query(int x) { 32 int l = 1 << x , r = ( 1 << ( x + 1 ) ) - 1 , ret = 0; 33 ret += bit[x].query( min( lim - 1 , max( 0ll , r - ( sum & ((1<<(x+1))-1) ) + 1 ) ) ); 34 ret -= bit[x].query( min( lim - 1 , max( 0ll , l - ( sum & ((1<<(x+1))-1) ) ) ) ); 35 l |= 1 << ( x + 1 ) , r |= 1 << ( x + 1 ); 36 ret += bit[x].query( min( lim - 1 , max( 0ll , r - ( sum & ((1<<(x+1))-1) ) + 1 ) ) ); 37 ret -= bit[x].query( min( lim - 1 , max( 0ll , l - ( sum & ((1<<(x+1))-1) ) ) ) ); 38 return ret; 39 } 40 41 inline char nextchar() { 42 static const int BS = 1 << 21; 43 static char buf[BS],*st,*ed; 44 if( st == ed ) ed = buf + fread(st=buf,1,BS,stdin); 45 return st == ed ? -1 : *st++; 46 } 47 inline int getint() { 48 int ret = 0 , ch , fix = 1; 49 while( !isdigit(ch=nextchar()) ) fix = ch == '-' ? -fix : fix; 50 do ret = ret * 10 + ch - '0'; while( isdigit(ch=nextchar()) ); 51 return ret * fix; 52 } 53 54 int main() { 55 static int n; 56 static lli x; 57 n = getint(); 58 for(int i=1,o;i<=n;i++) { 59 o = getint() , x = getint(); 60 if( o == 2 ) sum += x; 61 else if( o == 0 ) x -= sum , app.insert(x) , update(x,1); 62 else if( o == 1 ) x -= sum , update(x,-(signed)app.count(x)) , app.erase(x); 63 else printf("%d\n",query(x)); 64 } 65 return 0; 66 }
T2:

这题我做过,「BZOJ5332: [Sdoi2018]旧试题」了解一下,此题终结。
代码:

1 #pragma GCC optimize("Ofast") 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<vector> 6 #include<cctype> 7 typedef long long int lli; 8 const int maxn=1e5+1e2,lim=1e5; 9 const lli mod = ( 1ll << 32 ); 10 11 struct Edge { int tar,lcm; }; 12 struct Node { int u,v,w; } ns[maxn*21]; 13 int mu[maxn]; 14 lli fa[maxn],fb[maxn],fc[maxn],ans; 15 int deg[maxn],mem[maxn]; 16 int a,b,c,n,m,ecnt; 17 std::vector<Edge> es[maxn]; 18 19 inline int gcd(int x,int y) { 20 register int t; 21 while( t = x % y ) x = y , y = t; 22 return y; 23 } 24 inline void sieve() { 25 static int prime[maxn/10],cnt; 26 static bool vis[maxn]; 27 mu[1] = 1; 28 for(int i=2;i<=lim;i++) { 29 if( !vis[i] ) prime[++cnt] = i , mu[i] = -1; 30 for(int j=1;j<=cnt&&(lli)i*prime[j]<=lim;j++) { 31 const int tar = i * prime[j]; 32 vis[tar] = 1; 33 if( i % prime[j] ) mu[tar] = -mu[i]; 34 else break; 35 } 36 } 37 } 38 39 inline void getf(lli* dst,int lim) { 40 for(int i=1;i<=lim;i++) for(int j=i;j<=lim;j+=i) dst[i] += lim / j; 41 } 42 inline void calc_single_point() { 43 for(int i=1;i<=m;i++) if( mu[i] ) ans += mu[i] * mu[i] * mu[i] * fa[i] * fb[i] * fc[i]; 44 } 45 inline void pre_ring() { 46 for(int g=1;g<=n;g++) for(int i=1;i*g<=n;i++) if( mu[i*g] ) for(int j=i+1;(lli)i*j*g<=n;j++) if( mu[j*g] && gcd(i,j) == 1 ) { 47 const int u = i * g , v = j * g , w = i * j * g , pi = mu[u] * mu[u] * mu[v] , qi = mu[u] * mu[v] * mu[v]; 48 if( w > n ) continue; 49 ans += pi * ( fa[u] * fb[w] * fc[w] + fa[w] * fb[u] * fc[w] + fa[w] * fb[w] * fc[u] ); 50 ans += qi * ( fa[v] * fb[w] * fc[w] + fa[w] * fb[v] * fc[w] + fa[w] * fb[w] * fc[v] ); 51 ++deg[u] , ++deg[v] , ns[++ecnt] = (Node){u,v,w}; 52 } 53 for(int i=1;i<=ecnt;i++) { 54 if( deg[ns[i].u] < deg[ns[i].v] || ( deg[ns[i].u] == deg[ns[i].v] && ns[i].u < ns[i].v ) ) es[ns[i].u].push_back((Edge){ns[i].v,ns[i].w}); 55 else es[ns[i].v].push_back((Edge){ns[i].u,ns[i].w}); 56 } 57 } 58 inline void calc_ring() { 59 for(int i=1;i<=n;i++) { 60 for(unsigned J=0;J<es[i].size();J++) mem[es[i][J].tar] = es[i][J].lcm; 61 for(unsigned J=0;J<es[i].size();J++) { 62 const int j = es[i][J].tar; 63 for(unsigned K=0;K<es[j].size();K++) { 64 const int k = es[j][K].tar , pi = mu[i] * mu[j] * mu[k]; 65 const int lij = es[i][J].lcm , ljk = es[j][K].lcm , lki = mem[k]; 66 if( !lki ) continue; // lcm(i,k) > n so i didn't record k . 67 ans += pi * ( fa[lij] * fb[ljk] * fc[lki] + fa[lij] * fb[lki] * fc[ljk] + fa[ljk] * fb[lij] * fc[lki] + 68 fa[ljk] * fb[lki] * fc[lij] + fa[lki] * fb[lij] * fc[ljk] + fa[lki] * fb[ljk] * fc[lij] ); 69 } 70 } 71 for(unsigned J=0;J<es[i].size();J++) mem[es[i][J].tar] = 0; 72 } 73 } 74 75 inline void init() { 76 n = std::max( a , std::max( b , c ) ) , m = std::min( a , std::min( b , c ) ) , ans = 0; 77 } 78 79 inline int getint() { 80 int ret = 0 , ch; 81 while( !isdigit(ch=getchar()) ); 82 do ret = ret * 10 + ch - '0'; while( isdigit(ch=getchar()) ); 83 return ret; 84 } 85 86 int main() { 87 static int T; 88 a = getint() , b = getint() , c = getint() , init() , sieve() , getf(fa,a) , getf(fb,b) , getf(fc,c); 89 calc_single_point() , pre_ring() , calc_ring() , printf("%lld\n",ans%mod); 90 return 0; 91 }
T3:

这题,我......没做过。
这种期望一看就是假期望,其实就是统计贡献然后除总方案数。
于是我想到了一个暴力DP:
我们令f(i,j)表示i个不同的点分成j个联通块的方案数,我们有: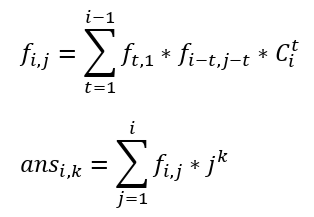
然后想了半天怎么优化,想不出来,10分弃疗。
正解根本不是这么做的......
首先《具体数学》告诉我们: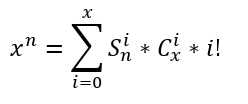
其中S(n,i)为第二类斯特林数,表示把n个点划分成i个不同的集合的方案数。
(考虑左边是n个不同球x个不同盒子随便放的方案数,右边先钦定用几个盒子,选出盒子并排列,把球分开然后放进去的方案数,正确性显然)
我们令f(i,j)表示i个点x次的贡献,如果分成了j个联通块,则贡献为下面的val,考虑贡献的组合意义(联通块间有序),我们得到f的转移和答案的计算公式: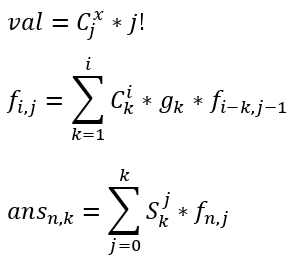
其中g(i)表示g个点的联通块方案数,怎么求?「BZOJ3456: 城市规划」了解一下。
把组合数拆开,显然就是卷积了。最后是斯特林数的递推问题了: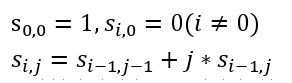
注意一下初值,然后就能AC啦。
考场10分代码:

1 #pragma GCC optimize("Ofast") 2 #include<iostream> 3 #include<cstdio> 4 #include<cstring> 5 #include<algorithm> 6 typedef long long int lli; 7 using namespace std; 8 const int maxn=512; 9 const int mod=1004535809; 10 11 inline int add(const int &x,const int &y) { 12 const int ret = x + y; 13 return ret >= mod ? ret - mod : ret; 14 } 15 inline int mul(const int &x,const int &y) { 16 return (lli) x * y % mod; 17 } 18 inline void adde(int &dst,const int &x) { 19 if( ( dst += x ) >= mod ) dst -= mod; 20 } 21 inline void sube(int &dst,const int &x) { 22 if( ( dst -= x ) < 0 ) dst += mod; 23 } 24 inline void mule(int &dst,const int &x) { 25 dst = (lli) dst * x % mod; 26 } 27 inline int fastpow(int base,int tim) { 28 int ret = 1; 29 while(tim) { 30 if( tim & 1 ) mule(ret,base); 31 if( tim >>= 1 ) mule(base,base); 32 } 33 return ret; 34 } 35 36 int f[maxn][maxn],c[maxn][maxn],mem[maxn][17]; 37 38 int main() { 39 c[0][0] = 1; 40 for(int i=1;i<maxn;i++) { 41 c[i][0] = 1; 42 for(int j=1;j<=i;j++) c[i][j] = add(c[i-1][j-1],c[i-1][j]); 43 } 44 f[1][1] = 1; 45 for(int i=2;i<maxn;i++) { 46 f[i][i] = 1; 47 for(int j=i-1;j>=1;j--) { 48 for(int t=1;t<=i;t++) adde(f[i][j],mul(mul(f[t][1],c[i][t]),f[i-t][j-1])); 49 mule(f[i][j],fastpow(j,mod-2)); 50 } 51 f[i][1] = fastpow(2,i*(i-1)>>1); 52 for(int j=2;j<=i;j++) sube(f[i][1],f[i][j]); 53 } 54 int t; 55 scanf("%d",&t) , memset(mem,-1,sizeof(mem)); 56 while(t--) { 57 int n,k,ans=0; 58 scanf("%d%d",&n,&k); 59 if( ~mem[n][k] ) printf("%d\n",mem[n][k]); 60 else { 61 for(int i=1;i<=n;i++) adde(ans,mul(f[n][i],fastpow(i,k))); 62 mule(ans,fastpow(fastpow(2,n*(n-1)>>1),mod-2)) , printf("%d\n",mem[n][k]=ans); 63 } 64 } 65 return 0; 66 }
正解代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #define debug cout 6 typedef long long int lli; 7 using namespace std; 8 const int maxn=131073; 9 const int mod=1004535809,G=3; 10 11 inline int add(const int &x,const int &y) { 12 const int ret = x + y; 13 return ret >= mod ? ret - mod : ret; 14 } 15 inline int sub(const int &x,const int &y) { 16 const int ret = x - y; 17 return ret < 0 ? ret + mod : ret; 18 } 19 inline int mul(const int &x,const int &y) { 20 return (lli) x * y % mod; 21 } 22 inline void adde(int &dst,const int &x) { 23 if( ( dst += x ) >= mod ) dst -= mod; 24 } 25 inline void mule(int &dst,const int &x) { 26 dst = (lli) dst * x % mod; 27 } 28 29 inline int fastpow(int base,int tim) { 30 int ret = 1; 31 while(tim) { 32 if( tim & 1 ) mule(ret,base); 33 if( tim >>= 1 ) mule(base,base); 34 } 35 return ret; 36 } 37 inline void NTT(int* dst,int n,int tpe) { 38 for(int i=0,j=0;i<n;i++) { 39 if( i < j ) swap(dst[i],dst[j]); 40 for(int t=n>>1;(j^=t)<t;t>>=1) ; 41 } 42 for(int len=2,h=1;len<=n;len<<=1,h<<=1) { 43 int per = fastpow(G,mod/len); 44 if( !~tpe ) per = fastpow(per,mod-2); 45 for(int st=0;st<n;st+=len) { 46 int w = 1; 47 for(int pos=0;pos<h;pos++) { 48 const int u = dst[st+pos] , v = mul(dst[st+pos+h],w); 49 dst[st+pos] = add(u,v) , dst[st+pos+h] = sub(u,v) , mule(w,per); 50 } 51 } 52 } 53 if( !~tpe ) { 54 const int inv = fastpow(n,mod-2); 55 for(int i=0;i<n;i++) mule(dst[i],inv); 56 } 57 } 58 inline void INV(int* dst,const int* sou,int len) { 59 static int tp[maxn]; 60 if( len == 1 ) return void( *dst = fastpow(*sou,mod-2) ); 61 INV(dst,sou,len>>1) , memcpy(tp,sou,len<<2) , memset(tp+len,0,len<<2); 62 NTT(dst,len<<1,1) , NTT(tp,len<<1,1); 63 for(int i=0;i<len<<1;i++) dst[i] = mul(dst[i],sub(2,mul(dst[i],tp[i]))); 64 NTT(dst,len<<1,-1) , memset(dst+len,0,len<<2); 65 } 66 67 int fac[maxn],inv[maxn],strl[21][21]; 68 inline int c(int n,int m) { 69 return mul(fac[n],mul(inv[m],inv[n-m])); 70 } 71 72 int f[16][maxn],g[maxn],ways[maxn]; 73 const int len = 65536; 74 75 namespace GetG { 76 int b[maxn],c[maxn],invb[maxn]; 77 inline void work() { 78 for(int i=0;i<len;i++) b[i] = mul(ways[i],inv[i]); 79 for(int i=1;i<len;i++) c[i] = mul(ways[i],inv[i-1]); 80 INV(invb,b,len) , NTT(invb,len<<1,1) , NTT(c,len<<1,1); 81 for(int i=0;i<len<<1;i++) g[i] = mul(invb[i],c[i]); 82 NTT(g,len<<1,-1) , g[0] = 0 , memset(g+len,0,len<<2); 83 for(int i=1;i<len;i++) mule(g[i],fac[i-1]); 84 } 85 } 86 87 namespace GetF { 88 inline void work() { 89 for(int i=1;i<len;i++) mule(g[i],inv[i]); 90 for(int i=0;i<len;i++) f[0][i] = mul(ways[i],inv[i]); 91 NTT(g,len<<1,1) , NTT(f[0],len<<1,1); 92 for(int j=1;j<16;j++) { 93 for(int i=0;i<len<<1;i++) f[j][i] = mul(f[j-1][i],g[i]); 94 NTT(f[j],len<<1,-1) , memset(f[j]+len,0,len<<2) , NTT(f[j],len<<1,1); 95 } 96 for(int j=0;j<16;j++) { 97 NTT(f[j],len<<1,-1); 98 for(int i=0;i<len;i++) mule(f[j][i],fac[i]); 99 } 100 } 101 } 102 103 inline int getans(int n,int k) { 104 int ret = 0; 105 for(int i=0;i<=k;i++) adde(ret,mul(f[i][n],strl[k][i])); 106 return ret; 107 } 108 109 inline void pre() { 110 *fac = 1; for(int i=1;i<len;i++) fac[i] = mul(fac[i-1],i); 111 inv[len-1] = fastpow(fac[len-1],mod-2); for(int i=len-1;i;i--) inv[i-1] = mul(inv[i],i); 112 for(int i=0;i<len;i++) ways[i] = fastpow(2,((lli)i*(i-1)>>1)%(mod-1)); 113 strl[0][0] = 1; 114 for(int i=1;i<16;i++) { 115 strl[i][0] = 0; 116 for(int j=1;j<=i;j++) strl[i][j] = add(strl[i-1][j-1],mul(j,strl[i-1][j])); 117 } 118 } 119 120 int main() { 121 static int t,n,k; 122 pre() , GetG::work() , GetF::work(); 123 scanf("%d",&t); 124 while(t--) scanf("%d%d",&n,&k) , printf("%d\n",mul(getans(n,k),fastpow(ways[n],mod-2))); 125 return 0; 126 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号