20180615小测
我居然学会WA题了!?
T1:
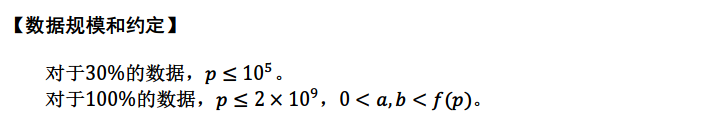
首先我们能打表观察或者数学推导得到在x为质数时f(x)=x,否则f(x)=2。
之后就是一个裸的k次剩余,也就是Bzoj1319了。
这个东西怎么做?假设我们要求解x^k=a(mod p),我们能求出p的原根g,并用BSGS求出a=g^n(mod p)。
假设x=g^t,那么我们有:t*k=n(mod phip),我们要求出所有可行的t。
然后就十分显然了,exgcd求出kx+yphip=gcd(k,phip),如果n不是gcd(k,phip)则显然无解,否则我们能以n/gcd(k,phip)*x为初值,x%(phip/gcd(phip,k))为步长不断递增求出所有可行的t。
注意特判掉p=2的情况,就可以AC啦。
代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 #include<tr1/unordered_map> 7 #include<cassert> 8 #define debug cout 9 typedef long long int lli; 10 using namespace std; 11 using namespace tr1; 12 const int maxn=5e5+1e2; 13 14 lli ans[maxn],anslen; 15 lli a,b,p,g; 16 17 inline bool isprime(lli x) { 18 const lli sq = sqrt(x); 19 for(lli i=2;i<=sq;i++) if( ! ( x % i ) ) return 0; 20 return 1; 21 } 22 23 inline lli fastpow(lli base,lli tim,lli mod) { 24 lli ret = 1; 25 while(tim) { 26 if( tim & 1 ) ret = ret * base % mod; 27 if( tim >>= 1 ) base = base * base % mod; 28 } 29 return ret; 30 } 31 inline lli exgcd(lli a,lli b,lli &x,lli &y) { 32 if( !b ) return x = 1 , y = 0 , a; 33 lli ret = exgcd(b,a%b,y,x); 34 return y -= a / b * x , ret; 35 } 36 37 namespace BSGS { 38 inline lli BSGS(lli a,lli b) { 39 const lli sq = sqrt(p); 40 unordered_map<lli,lli> mp; 41 lli step = 1 , giant = 1; 42 for(lli i=0;i<sq;i++) { 43 if( mp.find(step) == mp.end() ) mp[step] = i; 44 step = step * a % p; 45 } 46 for(lli i=0;i<=sq;i++) { 47 const lli ned = b * fastpow(giant,p-2,p) % p; 48 if( mp.find(ned) != mp.end() ) return sq * i + mp[ned]; 49 giant = giant * step % p; 50 } 51 assert(0); 52 } 53 } 54 55 namespace GetPrimaryRoot { 56 lli dvs[maxn],cnt; 57 inline void cut(lli t) { 58 const lli sq = sqrt(t); 59 for(lli i=2;i<=sq;i++) { 60 if( ! ( t % i ) ) { 61 dvs[++cnt] = i; 62 while( ! ( t % i ) ) t /= i; 63 } 64 } 65 if( t != 1 ) dvs[++cnt] = t; 66 } 67 inline bool judge(lli x) { 68 for(lli i=1;i<=cnt;i++) if( fastpow(x,(p-1)/dvs[i],p) == 1 ) return 0; 69 return 1; 70 } 71 inline lli getroot() { 72 for(lli i=1;i<p;i++) if( judge(i) ) return i; 73 assert(0); 74 } 75 } 76 77 int main() { 78 static lli n,phi,x,y,gcd,step; 79 scanf("%lld%lld%lld",&a,&b,&p) , p = isprime(p) ? p : 2; 80 if( p == 2 ) return assert(b) , puts("1\n1") , 0; 81 GetPrimaryRoot::cut(p-1) , g = GetPrimaryRoot::getroot() , n = BSGS::BSGS(g,b); 82 phi = p - 1 , gcd = exgcd(a,phi,x,y); 83 if( n % gcd ) return puts("0") , 0; 84 step = phi / gcd , x = ( x % step + step ) % step , x = x * ( n / gcd ) % step; 85 while( x < phi ) ans[++anslen] = fastpow(g,x,p) , x += step; 86 if( !anslen ) return puts("0") , 0; 87 sort(ans+1,ans+1+anslen) , printf("%lld\n",anslen); 88 for(lli i=1;i<=anslen;i++) printf("%lld%c",ans[i],i!=anslen?' ':'\n'); 89 return 0; 90 }
T2:

子树修改,链询问,不改变形态,一眼树剖+dfs序。
通过树剖我们能把询问变成dfs序上的logn个区间。
然后就是怎么维护这个序列的问题了,如果我们把点看做横坐标x,白兔数量看做纵坐标y,那么我们要进行的就是区间赋值,区间把点放到一条线上。
(不知道大家怎么想,反正我不会用线段树或者kdtree做......)
考虑分块,块内用数据结构(我选择了非旋treap)维护横坐标为x的最大的y。
这样对于整块的修改w,我们打标记,整块修改b,我们打标记,非整块修改,我们暴力push标记然后重构整个块。
查询怎么办?
对于整块的查询,如果有w标记且w标记在区间内,返回区间最大的b,否则返回0。
对于整块的查询,如果没有w标记,就是经典的treap区间查询了。(注意如果有b标记也不能直接返回b,因为我们需要的区间在块内可能为空)。
对于非整块的查询,暴力。
这个东西的时间复杂度是O(nsqrt(n)log^2n),空间复杂度线性。但是由于树剖和非旋treap的常数都很小,于是就可以AC啦(踩爆标程的3个log)。
另外神仙lyy的复杂度和链上颜色数相关的算法也AC了......我能把他卡成n^2......辣鸡出题人不会造数据。
代码(又臭又长的蒟蒻码风就不要吐槽了):

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 #define debug cerr 7 typedef long long int lli; 8 using namespace std; 9 const int maxn=1e5+1e2,maxe=3e5+1e2,maxb=4e2+1e2; 10 11 int n,bs; 12 13 struct pii{int l,r;}; 14 struct RotatelessTreap { 15 int lson[maxn],rson[maxn],dat[maxn],mx[maxn],fix[maxn]; 16 lli pv[maxn]; 17 RotatelessTreap() { 18 for(int i=0;i<maxn;i++) fix[i] = i; 19 random_shuffle(fix,fix+maxn); 20 } 21 inline void maintain(int pos) { 22 mx[pos] = max( dat[pos] , max(mx[lson[pos]],mx[rson[pos]]) ); 23 } 24 inline pii split(int pos,lli nv) { // left is <= nv . 25 if( !pos ) return (pii){0,0}; 26 if( pv[pos] > nv ) { // split pos to right . 27 pii spl = split(lson[pos],nv); 28 lson[pos] = spl.r , maintain(pos); 29 return (pii){spl.l,pos}; 30 } else { 31 pii spr = split(rson[pos],nv); 32 rson[pos] = spr.l , maintain(pos); 33 return (pii){pos,spr.r}; 34 } 35 } 36 inline int merge(int x,int y) { 37 if( !x || !y ) return x | y; 38 if( fix[x] > fix[y] ) { 39 rson[x] = merge(rson[x],y) , maintain(x); 40 return x; 41 } else { 42 lson[y] = merge(x,lson[y]) , maintain(y); 43 return y; 44 } 45 } 46 inline void reset(int pos,lli p,int d) { 47 lson[pos] = rson[pos] = 0 , pv[pos] = p , dat[pos] = mx[pos] = d; 48 } 49 inline void insert_node(int &root,int t) { 50 pii sp = split(root,pv[t]); 51 root = merge(sp.l,merge(t,sp.r)); 52 } 53 inline pii query_seg(int &root,lli ll,lli rr) { // return pair<(bool)siz,max> of segment (ll,rr] . 54 pii spl = split(root,ll) , spr = split(spl.r,rr); 55 pii ret = (pii){spr.l,mx[spr.l]}; 56 root = merge(spl.l,merge(spr.l,spr.r)); 57 return ret; 58 } 59 }treap; 60 61 int iw[maxn],ib[maxn]; 62 int bel[maxn],st[maxb],ed[maxb],lazy_w[maxb],lazy_b[maxb],root[maxb]; 63 64 inline lli gid(int pos,int st,int iw) { // iw can't be zero . 65 return (lli) iw * bs + pos - st; 66 } 67 inline void rebuild_blk(int id) { 68 root[id] = 0; 69 for(int i=st[id];i<=ed[id];i++) { 70 treap.reset(i,gid(i,st[id],iw[i]),ib[i]) , treap.insert_node(root[id],i); 71 } 72 } 73 inline void push_all(int id) { 74 if( ~lazy_w[id] ) { 75 for(int i=st[id];i<=ed[id];i++) iw[i] = lazy_w[id]; 76 lazy_w[id] = -1; 77 } 78 if( ~lazy_b[id] ) { 79 for(int i=st[id];i<=ed[id];i++) ib[i] = lazy_b[id]; 80 lazy_b[id] = -1; 81 } 82 } 83 inline void full_apply_w(int id,int w) { 84 lazy_w[id] = w; 85 } 86 inline void full_apply_b(int id,int b) { 87 lazy_b[id] = b; 88 } 89 inline int full_query(int id,int l,int r) { 90 if( ~lazy_w[id] ) { 91 if( ! ( l <= lazy_w[id] && lazy_w[id] <= r ) ) return 0; 92 if( ~lazy_b[id] ) return lazy_b[id]; 93 return treap.mx[root[id]]; 94 } else { 95 lli ll = (lli) bs * l - 1 , rr = (lli) bs * ( r + 1 ) - 1; 96 pii t = treap.query_seg(root[id],ll,rr); 97 if( ~lazy_b[id] ) return t.l ? lazy_b[id] : 0; 98 else return t.r; 99 } 100 } 101 inline void part_apply_w(int id,int w,int l,int r) { 102 push_all(id) , l = max( l , st[id] ) , r = min( r , ed[id] ); 103 for(int i=l;i<=r;i++) iw[i] = w; 104 rebuild_blk(id); 105 } 106 inline void part_apply_b(int id,int b,int l,int r) { 107 push_all(id) , l = max( l , st[id] ) , r = min( r , ed[id] ); 108 for(int i=l;i<=r;i++) ib[i] = b; 109 rebuild_blk(id); 110 } 111 inline int part_query(int id,int l,int r,int segl,int segr) { 112 segl = max( segl , st[id] ) , segr = min( segr , ed[id] ); 113 if( ~lazy_w[id] ) { 114 if( ! ( l <= lazy_w[id] && lazy_w[id] <= r ) ) return 0; 115 if( ~lazy_b[id] ) return lazy_b[id]; 116 int ret = 0; 117 for(int i=segl;i<=segr;i++) ret = max( ret , ib[i] ); 118 return ret; 119 } else { 120 if( ~lazy_b[id] ) { 121 for(int i=segl;i<=segr;i++) if( l <= iw[i] && iw[i] <= r ) return lazy_b[id]; 122 return 0; 123 } else { 124 int ret = 0; 125 for(int i=segl;i<=segr;i++) if( l <= iw[i] && iw[i] <= r ) ret = max( ret , ib[i] ); 126 return ret; 127 } 128 } 129 } 130 inline int query_seg(int l,int r,int ll,int rr) { // ll , rr is value segment . 131 if( bel[l] == bel[r] ) return part_query(bel[l],ll,rr,l,r); 132 else { 133 int ret = max( part_query(bel[l],ll,rr,l,r) , part_query(bel[r],ll,rr,l,r) ); 134 for(int i=bel[l]+1;i<bel[r];i++) ret = max( ret , full_query(i,ll,rr) ); 135 return ret; 136 } 137 } 138 inline void apply_seg_w(int l,int r,int w) { 139 if( bel[l] == bel[r] ) return part_apply_w(bel[l],w,l,r); 140 else { 141 part_apply_w(bel[l],w,l,r) , part_apply_w(bel[r],w,l,r); 142 for(int i=bel[l]+1;i<bel[r];i++) full_apply_w(i,w); 143 } 144 } 145 inline void apply_seg_b(int l,int r,int b) { 146 if( bel[l] == bel[r] ) return part_apply_b(bel[l],b,l,r); 147 else { 148 part_apply_b(bel[l],b,l,r) , part_apply_b(bel[r],b,l,r); 149 for(int i=bel[l]+1;i<bel[r];i++) full_apply_b(i,b); 150 } 151 } 152 153 int s[maxn],t[maxn<<1],nxt[maxn<<1]; 154 int fa[maxn],siz[maxn],dep[maxn],son[maxn],top[maxn],dfn[maxn],rit[maxn]; 155 156 inline void coredge(int from,int to) { 157 static int cnt; 158 t[++cnt] = to , nxt[cnt] = s[from] , s[from] = cnt; 159 } 160 inline void addedge(int a,int b) { 161 coredge(a,b) , coredge(b,a); 162 } 163 inline void pre(int pos) { 164 siz[pos] = 1; 165 for(int at=s[pos];at;at=nxt[at]) if( t[at] != fa[pos] ) { 166 dep[t[at]] = dep[pos] + 1 , fa[t[at]] = pos , pre(t[at]) , siz[pos] += siz[t[at]]; 167 if( siz[t[at]] > siz[son[pos]] ) son[pos] = t[at]; 168 } 169 } 170 inline void dfs(int pos) { 171 static int dd; 172 dfn[pos] = ++dd , top[pos] = pos == son[fa[pos]] ? top[fa[pos]] : pos; 173 if( son[pos] ) dfs(son[pos]); 174 for(int at=s[pos];at;at=nxt[at]) if( t[at] != fa[pos] && t[at] != son[pos] ) dfs(t[at]); 175 rit[pos] = dd; 176 } 177 178 inline void apply_subtree_w(int pos,int w) { 179 apply_seg_w(dfn[pos],rit[pos],w); 180 } 181 inline void apply_subtree_b(int pos,int b) { 182 apply_seg_b(dfn[pos],rit[pos],b); 183 } 184 inline int query_chain(int x,int y,int ll,int rr) { 185 int ret = 0; 186 while( top[x] != top[y] ) { 187 if( dep[top[x]] < dep[top[y]] ) swap(x,y); 188 ret = max( ret , query_seg(dfn[top[x]],dfn[x],ll,rr) ) , x = fa[top[x]]; 189 } 190 ret = max( ret , query_seg(min(dfn[x],dfn[y]),max(dfn[x],dfn[y]),ll,rr) ); 191 return ret; 192 } 193 194 inline void initblk() { 195 bs = sqrt(n); 196 for(int l=1,r,cnt=0;l<=n;l=r+1) { 197 r = min( l + bs - 1 , n ) , st[++cnt] = l , ed[cnt] = r , lazy_w[cnt] = lazy_b[cnt] = -1; 198 for(int i=l;i<=r;i++) bel[i] = cnt; 199 rebuild_blk(cnt); 200 } 201 } 202 203 int srt[maxn<<2],len; 204 int o[maxn],ox[maxn],oy[maxn],oll[maxn],orr[maxn]; 205 206 inline int gid(int x) { 207 return lower_bound(srt+1,srt+1+len,x) - srt; 208 } 209 210 int main() { 211 static int m; 212 static char ooo[50]; 213 scanf("%d%d",&n,&m); 214 for(int i=1,a,b;i<n;i++) scanf("%d%d",&a,&b) , addedge(a,b); 215 for(int i=1;i<=m;i++) { 216 scanf("%s%d%d",ooo+1,ox+i,oy+i); 217 if( ooo[1] == 'C' ) { 218 if( ooo[7] == 'W' ) o[i] = 1 , srt[++len] = oy[i]; 219 else o[i] = 2; 220 } else o[i] = 3 , scanf("%d%d",oll+i,orr+i) , srt[++len] = oll[i] , srt[++len] = orr[i]; 221 } 222 sort(srt+1,srt+1+len) , len = unique(srt+1,srt+1+len) - srt - 1; 223 for(int i=1;i<=m;i++) { 224 if( o[i] == 1 ) oy[i] = gid(oy[i]); 225 else if( o[i] == 3 ) oll[i] = gid(oll[i]) , orr[i] = gid(orr[i]); 226 } 227 pre(1) , dfs(1) , initblk(); 228 for(int i=1;i<=m;i++) { 229 if( o[i] == 1 ) apply_subtree_w(ox[i],oy[i]); 230 else if( o[i] == 2 ) apply_subtree_b(ox[i],oy[i]); 231 else printf("%d\n",query_chain(ox[i],oy[i],oll[i],orr[i])); 232 } 233 return 0; 234 }
T3:

这题我想了一个针对60分错误算法,爆零了......(另外这个题的前20%数据是不满足60%限制的,也就是说60%限制根本不够,辣鸡出题人不会造数据X2)
大概就是这样,f[i][x][y][s]表示i步在坐标(x,y),状态为s的最小值(显然i最大是nm),转移的话枚举怎么走,用队列存储状态加剪枝在随机数据下快到飞起。
看起来很有道理的样子,然而它是WA的,因为这样只能DP出一条简单路径的方案,但是最优方案可能不是一条路径(比如一个T形)。
正解是这样的:
我太菜了连斯坦纳树都看不出来了......
(话说我那个算法如果对的话斯坦纳树还有何用,心里就没点**吗)
随机化的话,随机数种子用老婆的名字,跑150次加上最优性剪枝,在Ofast加持下能卡进1.5s,踩爆std。
考场爆零代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<queue> 6 #define debug cout 7 using namespace std; 8 const int maxn=25,maxs=1<<9; 9 const int inf=0x3f3f3f3f; 10 const int dx[]={1,-1,0,0},dy[]={0,0,1,-1}; 11 12 int bin[maxs]; 13 struct Node {int x,y,s;}; 14 int a[maxn][maxn],b[maxn][maxn]; 15 int f[2][maxn][maxn][maxs]; 16 bool inq[2][maxn][maxn][maxs]; 17 queue<Node> q[2]; 18 int n,m,k,cur,ans; 19 20 inline void update(int &dst,const int &x) { 21 dst = min( dst , x ); 22 } 23 inline void trans() { // it works well under random input data . 24 #define legal(x,y) (0<=x&&x<n&&0<=y&&y<m) 25 while( q[cur^1].size() ) { 26 const int x = q[cur^1].front().x , y = q[cur^1].front().y , s = q[cur^1].front().s; q[cur^1].pop(); 27 for(int i=0;i<4;i++) { 28 const int tx = x + dx[i] , ty = y + dy[i]; 29 if( legal(tx,ty) && ~a[tx][ty]) { 30 const int ts = s | ( 1 << a[tx][ty] ) , tf = f[cur^1][x][y][s] + b[tx][ty]; 31 if( bin[ts] >= k ) update(ans,tf); 32 if( tf < ans ) { 33 update(f[cur][tx][ty][ts],tf); 34 if( !inq[cur][tx][ty][ts] ) q[cur].push((Node){tx,ty,ts}) , inq[cur][tx][ty][ts] = 1; 35 } 36 } 37 } 38 f[cur^1][x][y][s] = inf , inq[cur^1][x][y][s] = 0; 39 } 40 #undef legal 41 } 42 43 int main() { 44 static int T; 45 scanf("%d",&T) , memset(f,0x3f,sizeof(f)); 46 for(int i=1;i<maxs;i++) bin[i] = bin[i>>1] + ( i & 1 ); 47 while(T--) { 48 scanf("%d%d%d",&n,&m,&k) , cur = 0 , ans = inf; 49 if( !k ) { puts("0"); continue; } 50 for(int i=0;i<n;i++) for(int j=0;j<m;j++) scanf("%d",a[i]+j); 51 for(int i=0;i<n;i++) for(int j=0;j<m;j++) scanf("%d",b[i]+j); 52 for(int i=0;i<n;i++) for(int j=0;j<m;j++) if( ~a[i][j] ) { 53 f[cur][i][j][1<<a[i][j]] = b[i][j]; 54 if( !inq[cur][i][j][1<<a[i][j]] ) q[cur].push((Node){i,j,1<<a[i][j]}); 55 } 56 for(int i=2;i<=n*m;i++) cur ^= 1 , trans(); 57 printf("%d\n",ans==inf?-1:ans); 58 } 59 return 0; 60 }
正解代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<queue> 6 #define debug cout 7 using namespace std; 8 const int maxn=26,maxs=1<<5; 9 const int inf=0x3f3f3f3f; 10 const int dx[]={1,-1,0,0},dy[]={0,0,1,-1}; 11 12 struct Node{int x,y;}; 13 int a[maxn][maxn],b[maxn][maxn],fakea[maxn][maxn]; 14 int f[maxs][maxn][maxn]; 15 int n,m,k,fs,ans; 16 17 inline void spfa(int dis[maxn][maxn]) { 18 static bool inq[maxn][maxn]; 19 queue<Node> q; 20 #define legal(x,y) (0<x&&x<=n&&0<y&&y<=m) 21 for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if( dis[i][j] < ans ) q.push((Node){i,j}); 22 while( q.size() ) { 23 const int x = q.front().x , y = q.front().y; q.pop() , inq[x][y] = 0; 24 for(int i=0;i<4;i++) { 25 const int tx = x + dx[i] , ty = y + dy[i]; 26 if( legal(tx,ty) && ~fakea[tx][ty] && dis[tx][ty] > dis[x][y] + b[tx][ty] ) { 27 dis[tx][ty] = dis[x][y] + b[tx][ty]; 28 if( dis[tx][ty] >= ans ) { dis[tx][ty] = inf; continue; } 29 if( !inq[tx][ty] ) q.push((Node){tx,ty}); 30 } 31 } 32 } 33 } 34 inline int solve() { 35 int ret = inf; 36 memset(f,0x3f,sizeof(f)) , fs = 1 << k; 37 for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if( ~fakea[i][j] ) f[1<<fakea[i][j]][i][j] = b[i][j]; 38 for(int i=0;i<fs;i++) { 39 for(int j=i;j;j=(j-1)&i) for(int x=1;x<=n;x++) for(int y=1;y<=m;y++) if( ~fakea[i][j] ) 40 f[i][x][y] = min( f[i][x][y] , f[j][x][y] + f[i^j][x][y] - b[x][y] ); 41 spfa(f[i]); 42 } 43 for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) ret = min( ret , f[fs-1][i][j] ); 44 return ret; 45 } 46 inline void gen() { 47 static int ls[maxn*maxn]; 48 for(int i=0;i<=n*m;i++) ls[i] = rand() % k; 49 for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) fakea[i][j] = (~a[i][j]) ? ls[a[i][j]] : -1; 50 } 51 inline void getans() { 52 for(int i=1;i<=150;i++) gen() , ans = min( ans , solve() ); 53 } 54 55 inline void init() { 56 static const char seed[] = "KurenaiKisaragi"; 57 int su = 0 , li = strlen(seed); 58 for(int i=0;i<li;i++) su += seed[i]; 59 srand(su); 60 } 61 62 int main() { 63 static int T; 64 scanf("%d",&T) , init(); 65 while(T--) { 66 scanf("%d%d%d",&n,&m,&k) , ans = inf; 67 for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) scanf("%d",a[i]+j); 68 for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) scanf("%d",b[i]+j); 69 getans() , printf("%d\n",ans==inf?-1:ans); 70 } 71 return 0; 72 }
这次又不是rank1了(还不是因为T3爆零),果然我还是太菜了啊。
这次之前的话,已经不知道多长时间没有在考场上WA题了呢......
I am waiting for you And looking for truth But not a sound is heard
我在等着 ,寻找着真相 但却听不到声音
Whenever you need any help and my voice Lease let me know
无论何时 只要你需要任何帮助和我的声音 请让我知道
Can I sing for you or cry for dream ?
我可以为你歌唱或者呼唤梦想么
Let the wind blow
让风吹吧
So I can see the sky
这样我就能看到天空



 浙公网安备 33010602011771号
浙公网安备 33010602011771号