20180611小测

T1:

注意下面的那个求平均值的公式少了一个除大小，自行补上。
这种数据范围的最小方差生成树？真的可做？
BZOJ3754那题我可是n^2k暴力卡过去的啊......(好像只能暴力QAQ)
正解？标算好像就是求尽可能近的区间生成树。显然不对啊......
不可做，不可做。咕咕咕了。

T2: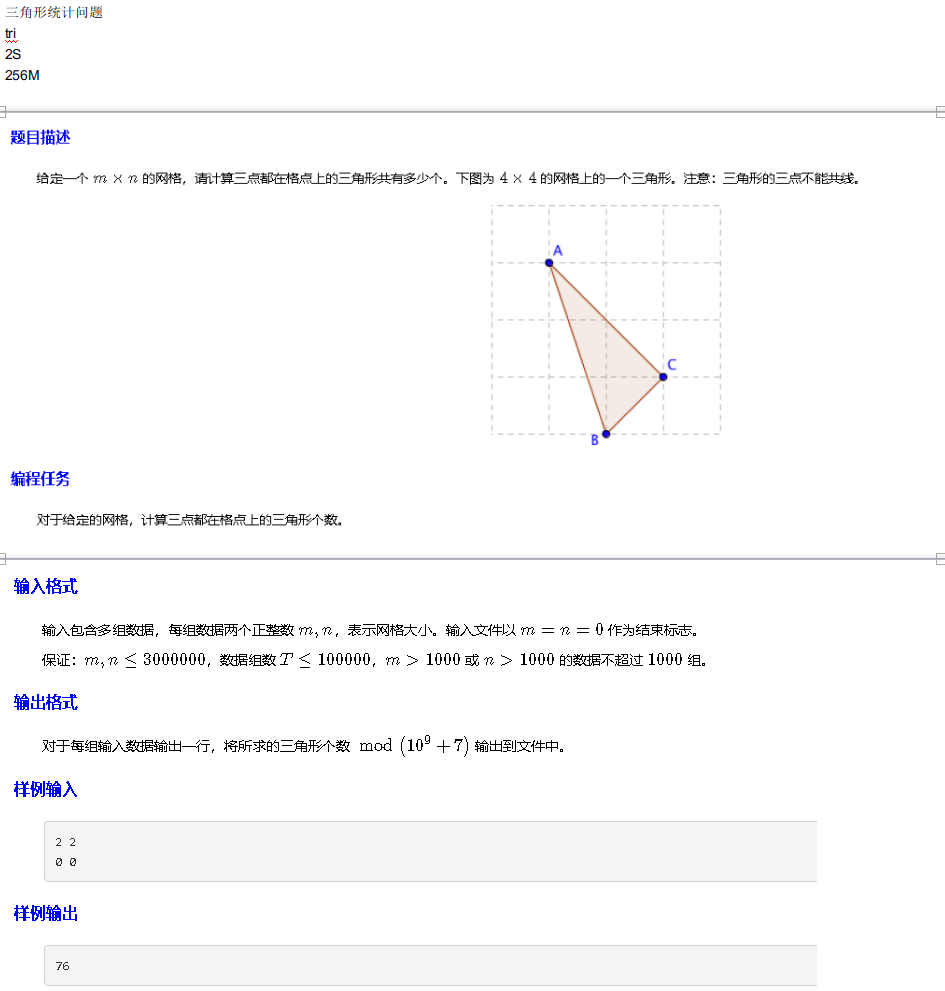

怎么又是原题？
真不是BZOJ3505吗？
考虑枚举所有选三个点的方案再减去三点共线的。
就是C(n*m,3)-m*C(n,3)-n*C(m,3)-2*sigma(i from 1 to n-1,j from 1 to m-1)(gcd(i,j)-1)(n-i)(m-j)。
也就是全部的方案数为C(n*m,3)，平行于坐标轴三点共线的有m*C(n,3)-n*C(m,3)种，斜向三点共线的，考虑枚举两边的两个点形成的向量，这样的向量存在(n-i)(m-j)个，对于每个向量，把中间点放置在格点上的方案有gcd(i,j)-1种，因为左右两种方向所以要全部*2。
但是，数据范围什么鬼......
考虑对公式进行数学变形:

右边的东西就很容易求和了(具体数学告诉你这样交换求和变量是对的):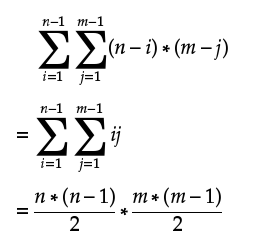

对于gcd反演的惯例反演就是变成phi啦(什么这步你推不出来？丢人！退役吧！)：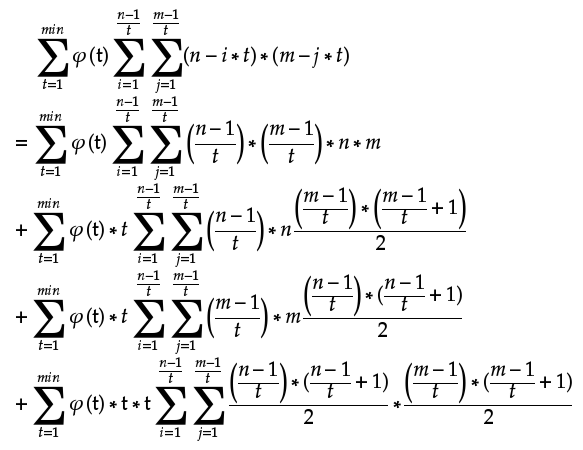

(不要吐槽我的公式渲染，msword2016在linux下就是这个德行)
由于求和式子的取值至于(n-1)/t和(m-1)/t有关，数论分块就很显然了。
然而卡常只有90分......
代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define debug cout
typedef long long int lli;
using namespace std;
const int maxn=3e6+1e2,lim=3e6;
const int mod=1e9+7,inv[]={0,1,500000004,333333336};

inline lli C3(lli x) {
    lli ret = 1; x %= mod;
    for(int i=0;i<3;i++) ret = ret * ( x - i + mod ) % mod , ret = ret * inv[i+1] % mod;
    return ret;
}
inline lli LSU(lli x) {
    return x * ( x + 1 ) % mod * inv[2] % mod;
}

lli phi[maxn],phix[maxn],phixx[maxn];
int n,m;

inline void sieve() {
    static int prime[maxn],cnt;
    static bool vis[maxn];
    phi[1] = 1;
    for(int i=2;i<=lim;i++) {
        if( !vis[i] ) prime[++cnt] = i , phi[i] = i - 1;
        for(int j=1;j<=cnt&&(lli)i*prime[j]<=lim;j++) {
            const int tar = i * prime[j];
            vis[tar] = 1;
            if( i % prime[j] ) phi[tar] = phi[i] * ( prime[j] - 1 );
            else { phi[tar] = phi[i] * prime[j]; break; }
        }
    }
    for(int i=1;i<=lim;i++) {
        phix[i] = phi[i] * i % mod , phixx[i] = phix[i] * i % mod;
        phi[i] = ( phi[i] + phi[i-1] ) % mod , phix[i] = ( phix[i] + phix[i-1] ) % mod , phixx[i] = ( phixx[i] + phixx[i-1] ) % mod;
    };
}

inline lli initans() {
    lli ret = ( ( C3((lli)n*m) - n * C3(m) - m * C3(n) ) % mod + mod ) % mod;
    ret = ( ret + LSU(n-1) * LSU(m-1) % mod * 2 % mod ) % mod;
    return ret;
}
inline lli getsub() { // assert n <= m .
    lli ret = 0;
    if( n > m ) swap(n,m);
    for(int i=1,j;i<n;i=j+1) {
        j = min( ( n - 1 ) / ( ( n - 1 ) / i ) , ( m - 1 ) / ( ( m - 1 ) / i ) );
        const lli apn = ( n - 1 ) / i , apm = ( m - 1 ) / i;
        ret += ( phi[j] - phi[i-1] + mod ) % mod * apn % mod * apm % mod * n % mod * m % mod , ret %= mod;
        ret += ( phixx[j] - phixx[i-1] + mod ) % mod * LSU(apn) % mod * LSU(apm) % mod , ret %= mod;
        ret -= ( phix[j] - phix[i-1] + mod ) % mod * LSU(apn) % mod * apm % mod * m % mod , ret = ( ret + mod ) % mod;
        ret -= ( phix[j] - phix[i-1] + mod ) % mod * LSU(apm) % mod * apn % mod * n % mod , ret = ( ret + mod ) % mod;
    }
    ret = ret * 2 % mod;
    return ret;
}

int main() {
    sieve();
    while( scanf("%d%d",&n,&m) == 2 && ( n || m ) ) n++ , m++ , printf("%lld\n",(initans()-getsub()+mod)%mod);
}

 

T3:

这题什么东西啊？真的可做？
写了一个三分套(线段树+RMQ+三分套二分)(什么鬼)，发现不符合单调性，就能过样例，对拍拍一组WA一组。
无奈写了个O(n^2logn)的暴力，放进去交了，骗了20分......
正解是这个样子的:

(表示您并没有告诉我数据随机)
但是，如果数据真的随机，并没有那么麻烦！
我可以写一个O(n^2)暴力，从右向左枚举左端点，然后从左向右枚举右端点，对于每个右端点，我么令sj表示当前左端点到j的区间的最小和。显然每次更新的时候sj=min(sj,sj-1,ai-aj)，于是就去掉log了。
这样暴力显然不能AC，我们能加入剪枝，如果当前sj*(n-i)已经<=答案了，我们就可以把内层循环break掉了。
然后就能AC啦！

考场20分代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<set>
#define debug cout
typedef long long int lli;
using namespace std;
const int maxn=1e5+1e2,lim=1e5;
const int inf=0x3f3f3f3f , minf = -inf;
const lli lli_inf = 0x3f3f3f3f3f3f3f3fll;

int in[maxn],n,k;

namespace Force {
    const int maxn=2e3+1e2;
    int f[maxn][maxn];
    multiset<int> ms;
    inline void work() {
        lli ans = -lli_inf;
        for(int i=1;i<=n;i++) {
            ms.clear() , ms.insert(in[i]) , f[i][i] = inf;
            for(int j=i+1;j<=n;j++) {
                f[i][j] = f[i][j-1];
                if( ms.find(in[j]) != ms.end() ) { f[i][j] = 0; continue; }
                multiset<int>::iterator it = ms.lower_bound(in[j]);
                if( it != ms.end() ) f[i][j] = min( f[i][j] , *it - in[j] );
                if( it != ms.begin() ) f[i][j] = min( f[i][j] , in[j] - *--it );
                if( j - i + 1 >= k ) ans = max( ans , (lli) f[i][j] * ( j - i ) );
                ms.insert(in[j]);
            }
        }
        printf("%lld\n",ans);
    }
}
namespace Sol {
    int Log[maxn],mxl;

    struct RMQ_Min {
        int dat[maxn][20];
        int& operator [] (const int &x) { return *dat[x]; }
        inline void rebuild() {
            for(int j=1;j<=mxl;j++) for(int i=1;i<=n;i++) dat[i][j] = min( dat[i][j-1] , dat[i+(1<<(j-1))][j-1] );
        }
        inline int query(int l,int r) {
            int L = Log[r-l+1];
            return min( dat[l][L] , dat[r-(1<<L)+1][L] );
        }
    }rmqmi;

    struct RMQ_Max {
        int dat[maxn][20];
        int& operator [] (const int &x) { return *dat[x]; }
        inline void rebuild() {
            for(int j=1;j<=mxl;j++) for(int i=1;i<=n;i++) dat[i][j] = max( dat[i][j-1] , dat[i+(1<<(j-1))][j-1] );
        }
        inline int query(int l,int r) {
            int L = Log[r-l+1];
            return max( dat[l][L] , dat[r-(1<<L)+1][L] );
        }
    }rmqmx;

    struct SemgnetTree_Min {
        int l[maxn<<3],r[maxn<<3],lson[maxn<<3],rson[maxn<<3],dat[maxn<<3],cnt;
        inline void build(int pos,int ll,int rr) {
            l[pos] = ll , r[pos] = rr , dat[pos] = inf;
            if( ll == rr ) return;
            const int mid = ( ll + rr ) >> 1;
            build(lson[pos]=++cnt,ll,mid) , build(rson[pos]=++cnt,mid+1,rr);
        }
        inline void update(int pos,const int &tar,const int &x) {
            if( l[pos] == r[pos] ) return void( dat[pos] = x );
            const int mid = ( l[pos] + r[pos] ) >> 1;
            tar <= mid ? update(lson[pos],tar,x) : update(rson[pos],tar,x) , dat[pos] = min( dat[lson[pos]] , dat[rson[pos]] );
        }
        inline int query(int pos,const int &ll,const int &rr) {
            if( ll <= l[pos] && r[pos] <= rr ) return dat[pos];
            const int mid = ( l[pos] + r[pos] ) >> 1;
            if( rr <= mid ) return query(lson[pos],ll,rr);
            else if( ll > mid ) return query(rson[pos],ll,rr);
            return min( query(lson[pos],ll,rr) , query(rson[pos],ll,rr) );
        }
        inline void reset() { cnt = 1; }
    }sgtmi;

    struct SemgnetTree_Max {
        int l[maxn<<3],r[maxn<<3],lson[maxn<<3],rson[maxn<<3],dat[maxn<<3],cnt;
        inline void build(int pos,int ll,int rr) {
            l[pos] = ll , r[pos] = rr , dat[pos] = minf;
            if( ll == rr ) return;
            const int mid = ( ll + rr ) >> 1;
            build(lson[pos]=++cnt,ll,mid) , build(rson[pos]=++cnt,mid+1,rr);
        }
        inline void update(int pos,const int &tar,const int &x) {
            if( l[pos] == r[pos] ) return void( dat[pos] = x );
            const int mid = ( l[pos] + r[pos] ) >> 1;
            tar <= mid ? update(lson[pos],tar,x) : update(rson[pos],tar,x) , dat[pos] = max( dat[lson[pos]] , dat[rson[pos]] );
        }
        inline int query(int pos,const int &ll,const int &rr) {
            if( ll <= l[pos] && r[pos] <= rr ) return dat[pos];
            const int mid = ( l[pos] + r[pos] ) >> 1;
            if( rr <= mid ) return query(lson[pos],ll,rr);
            else if( ll > mid ) return query(rson[pos],ll,rr);
            return max( query(lson[pos],ll,rr) , query(rson[pos],ll,rr) );
        }
        inline void reset() { cnt = 1; }
    }sgtmx;

    int liml[maxn],limr[maxn];

    inline bool judge(int l,int r) {
        int ll = rmqmx.query(l,r) , rr = rmqmi.query(l,r);
        return ll <= l && r <= rr;
    }
    inline int binrit(int curl,int l,int r) {
        if( judge(curl,r) ) return r;
        int mid;
        while( r > l + 1 ) {
            mid = ( l + r ) >> 1;
            if( judge(curl,mid) ) l = mid;
            else r = mid;
        }
        return l;
    }
    inline int triseg(int pos) { // if same move l .
        int l = liml[pos] , r = pos , lmid , rmid , tpl;
        int cl , cr , ret = -inf;
        while( r > l + 2 ) {
            lmid = ( l + l + r ) / 3 , rmid = ( l + r + r ) / 3;

            tpl = rmqmi.query(lmid,pos);
            if( tpl < pos ) cl = -inf;
            else cl = binrit(lmid,pos,limr[pos]) - lmid;

            tpl = rmqmi.query(rmid,pos);
            if( tpl < pos ) cr = -inf;
            else cr = binrit(rmid,pos,limr[pos]) - rmid;

            if( cl <= cr ) l = lmid;
            else r = rmid;
        }
        for(int i=l;i<=r;i++) {
            tpl = rmqmi.query(i,pos);
            if( tpl < pos ) continue;
            ret = max( ret , binrit(i,pos,limr[pos]) - i );
        }
        return ret;
    }
    inline int getmxseg(int lim) {
        int ret = -inf;
        sgtmi.reset() , sgtmi.build(1,1,1e5);
        for(int i=n;i;i--) limr[i] = rmqmi[i] = min(sgtmi.query(1,in[i]-lim+1,in[i]+lim-1)-1,n) , sgtmi.update(1,in[i],i);
        sgtmx.reset() , sgtmx.build(1,1,1e5);
        for(int i=1;i<=n;i++) liml[i] = rmqmx[i] = max(sgtmx.query(1,in[i]-lim+1,in[i]+lim-1)+1,1) , sgtmx.update(1,in[i],i);
        rmqmi.rebuild() , rmqmx.rebuild();
        for(int i=1;i<=n;i++) {
            ret = max( ret , triseg(i) );
        }
        return ret >= k ? ret : -inf;
    }
    inline lli tri1() { // WAWAWA
        int l = 1 , r = lim , lmid , rmid;
        lli cl , cr , ret = -lli_inf;
        while( r > l + 2 ) {
            lmid = ( l + l + r ) / 3 , rmid = ( l + r + r ) / 3;
            cl = (lli) lmid * getmxseg(lmid) , cr = (lli) rmid * getmxseg(rmid);
            if( cl <= cr ) l = lmid;
            else r = rmid;
        }
        for(int i=l;i<=r;i++) ret = max( ret , (lli) i * getmxseg(i) );
        return ret;
    }
    inline lli tri2() { // WAWAWA
        int l = 1 , r = lim , lmid , rmid;
        lli cl , cr , ret = -lli_inf;
        while( r > l + 2 ) {
            lmid = ( l + l + r ) / 3 , rmid = ( l + r + r ) / 3;
            cl = (lli) lmid * getmxseg(lmid) , cr = (lli) rmid * getmxseg(rmid);
            if( cl < cr ) l = lmid;
            else r = rmid;
        }
        for(int i=l;i<=r;i++) ret = max( ret , (lli) i * getmxseg(i) );
        return ret;
    }

    inline void getlog() {
        for(int i=2;i<=n;i++) Log[i] = Log[i>>1] + 1;
        mxl = Log[n];
    }

    inline void work() {
        --k , getlog() , printf("%lld\n",max(tri1(),tri2()));
    }
}

int main() {
    static int T;
    scanf("%d",&T);
    while(T--) {
        scanf("%d%d",&n,&k);
        for(int i=1;i<=n;i++) scanf("%d",in+i);
        if( n <= 3e3 ) Force::work();
        else Sol::work();
    }
    return 0;
}

正解代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#define debug cout
typedef long long int lli;
using namespace std;
const int maxn=1e5+1e2,lim=1e5,blk=1e3;
const int inf=0x3f3f3f3f , minf = -inf;
const lli lli_inf = 0x3f3f3f3f3f3f3f3fll;

int in[maxn],n,k;

namespace Force {
    int s[maxn];
    inline void work() {
        lli ans = -lli_inf;
        memset(s,0x3f,sizeof(s));
        for(int i=n;i;i--) {
            for(int j=i+1;j<=n/*&&j<=i+blk*/;j++) {
                s[j] = min( s[j] , abs(in[i]-in[j]) ) , s[j] = min( s[j] , s[j-1] );
                if( j - i >= k )ans = max( ans , (lli) s[j] * ( j - i ) );
                if( (lli) s[j] * ( n - i ) <= ans ) break;
            }
        }
        printf("%lld\n",ans);
    }
}

int main() {
    static int T;
    scanf("%d",&T);
    while(T--) {
        scanf("%d%d",&n,&k) , --k;
        for(int i=1;i<=n;i++) scanf("%d",in+i);
        Force::work();
    }
}

 

这种题都做不出来，果然还是我太菜啦！
对了我决定把电脑里的Win10删掉以彻底杜绝自己想要推gal的思想

冷(つめ)たかった 寂(さみ)しかった
好冷啊，好寂寞
凍(い)てつく街(まち)に息衝(いきづ)く
生活在这冰封的城镇里
優(やさ)しい愛(あい)の唄(うた)が
温柔地爱的歌谣
胸(むね)の奥(おく)積(つ)もって
在心中回响
変わる景色 幼い私 隔てた 境界線(きょうかいせん
将变化的景色和幼小的自己分隔的境界线
見(み)えなくなるくらい 染(そ)めていたの
变得不再那样清晰