20180507小测

对我而言相当失败的一次考试呢。
(昨天失了智一晚上没睡觉还好意思说)

T1: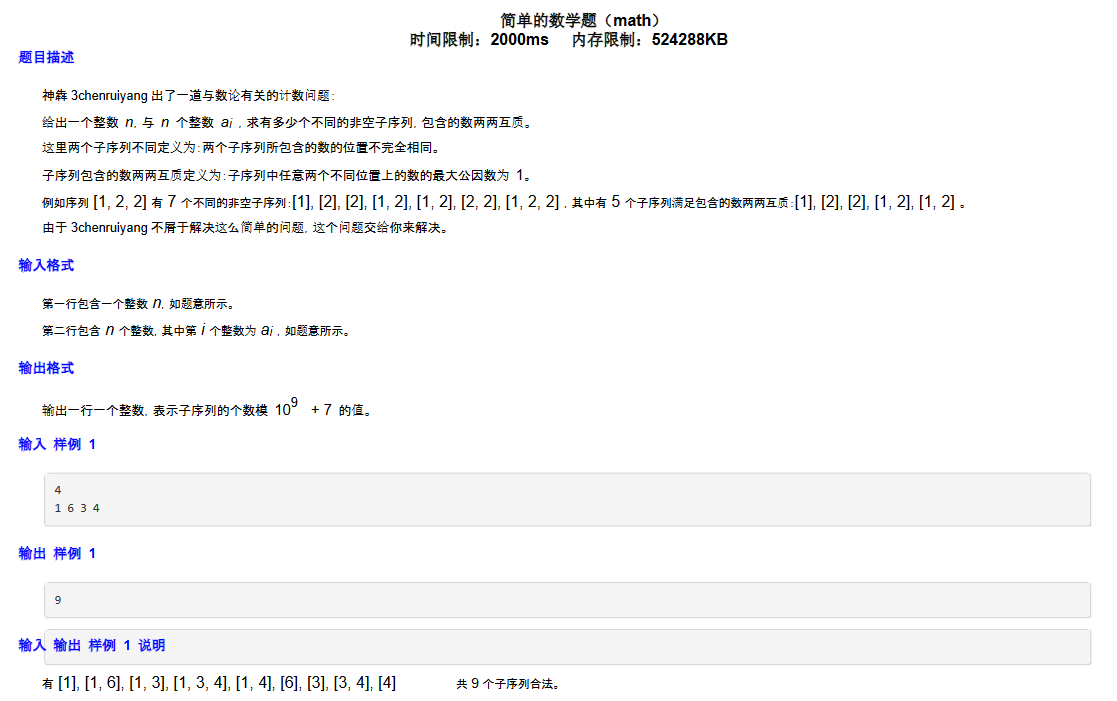

看到数据范围与值域有关，是不是想到了一些有趣的事情呢？
两两gcd为1，显然我们把同时选出的数分解质因子后，每个质数出现最多一次。是不是能状压DP呢？
(然后我发现2000内的质数有将近200个，没法状压，然后写了30分暴力)
这里有一个很显然的性质，数字x>=sqrt(x)的质因子最多只有1个，所以我们只需要状压<=sqrt(2000)的质因数，即{2-43}，只有14个。
其余的，我们能按照大质因子分组，然后每组最多选1个数字。
我们令f[i][sta]表示前i组，质因数状态为sta的方案数。转移的话可以枚举这组选择哪个数字，然后进行转移。
注意没有>43质因子的数字要各自一组，因为它们不存在互斥状态。
代码:

#include<cstdio>
#include<algorithm>
#include<vector>
typedef long long int lli;
const int maxn=2e3+1e2,maxs=(1<<14)+5;
const int prime[]={2,3,5,7,11,13,17,19,23,29,31,37,41,43},pl=14,full=1<<14;
const int mod=1e9+7;

struct Node {
    int sta,mx;
    friend bool operator < (const Node &a,const Node &b) { return a.mx > b.mx; }
}ns[maxn];

std::vector<Node> grp[maxn];
lli f[maxn][maxs],ans;
int n,cnt;

inline Node cut(int x) {
    int ret = 0;
    for(int i=0;i<pl;i++)
        if( ! ( x % prime[i] ) ) {
            ret |= (1<<i);
            while( ! ( x % prime[i] ) ) x /= prime[i];
        }
    return (Node){ret,x};
}

inline void getgrp() {
    std::sort(ns+1,ns+1+n);
    for(int i=1;i<=n;i++) {
        if( ns[i].mx != ns[i-1].mx || ns[i].mx == 1 ) ++cnt;
        grp[cnt].push_back(ns[i]);
    }
}
inline void dp() {
    **f = 1;
    for(int i=1;i<=cnt;i++) {
        for(unsigned cur=0;cur<grp[i].size();cur++)
            for(int sta=0;sta<full;sta++) {
                if( ! ( sta & grp[i][cur].sta ) )
                    f[i][sta|grp[i][cur].sta] = ( f[i][sta|grp[i][cur].sta] + f[i-1][sta] ) % mod;
                }
        for(int sta=0;sta<full;sta++) f[i][sta] = ( f[i][sta] + f[i-1][sta] ) % mod;
    }
    for(int i=0;i<full;i++) ans = ( ans + f[cnt][i] ) % mod;
}

int main() {
    scanf("%d",&n);
    for(int i=1,t;i<=n;i++) scanf("%d",&t) , ns[i] = cut(t);
    getgrp() , dp() , printf("%lld\n",(ans-1+mod)%mod);
    return 0;
}

T2:

字符串题，我只会后缀自动机......
很好，这题，后缀自动机不可做......然后我就GG了。
考虑SAM怎么做这道题，我们用可持久话线段树记录每个点的right集合，然后我们要找<=节点len的right集合中两个数的最大差......
这个东西由于存在自身对自身的贡献，所以没法启发式合并。
然后我就写了48分哈希。

考虑用后缀数组求LCP和LCS。
我们考虑枚举这个串的循环节的一半为i，然后在这个字符串中取1+k*i位置为关键点。
然后枚举两个相邻的关键点。显然如果有一个能满足条件的串存在的话，它一定是前一半过第一个关键点，后一半过第二个关键点的。
好的，我们可以求出这两个点的LCP和LCS之和，如果>=i的话，则证明存在长度>=i的满足条件的串。
复杂度为O(nlogn)，注意构造后缀数组不能用SAM，会MLE.....要么DC3或者后缀平衡树，要么老老实实写倍增(然而我不会倍增)。
爆内存的SAM:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define debug cout
using namespace std;
const int maxn=2e6+1e2,maxl=23;

char in[maxn>>1];
int Log[maxn>>1],li,ans;

struct SuffixAutomatic {
    int ch[maxn][26],tc[maxn][26],fa[maxn],len[maxn],rit[maxn],root,last,cnt;
    int stk[maxn],sa[maxn>>1],rnk[maxn>>1],h[maxn>>1],rmq[maxn>>1][maxl],top,sal;
    SuffixAutomatic() { last = root = cnt = 1; }
    inline int NewNode(int ll) {
        return len[++cnt] = ll , cnt;
    }
    inline void extend(int x,int r) {
        int p = last , np = NewNode(len[p]+1); rit[np] = r;
        while( p && !ch[p][x] ) ch[p][x] = np , p = fa[p];
        if( !p ) fa[np] = root;
        else {
            int q = ch[p][x];
            if( len[q] == len[p] + 1 ) fa[np] = q;
            else {
                int nq = NewNode(len[p]+1);
                memcpy(ch[nq],ch[q],sizeof(ch[q])) , fa[nq] = fa[q] , fa[np] = fa[q] = nq;
                while( p && ch[p][x] == q ) ch[p][x] = nq , p = fa[p];
            }
        }
        last = np;
    }
    inline void pre(int pos) {
        for(int i=0,t;i<26;i++) if( ( t = ch[pos][i] ) && len[t] == len[pos] + 1 ) {
            stk[++top] = i , tc[fa[t]][stk[len[t]-len[fa[t]]]] = t , pre(t) , stk[top--] = '\0';
        }
    }
    inline void dfs(int pos) {
        if( rit[pos] ) sa[++sal] = rit[pos];
        for(int i=0;i<26;i++) if( tc[pos][i] ) dfs(tc[pos][i]);
    }
    inline void geth(char* in,int li) {
        for(int i=1;i<=sal;i++) rnk[sa[i]] = i;
        reverse(in+1,in+1+li);
        for(int i=1,k=0;i<=sal;i++) {
            k -= (bool)k;
            const int p = sa[rnk[i]-1];
            while( in[i+k] == in[p+k] ) ++k;
            h[rnk[i]-1] = k;
        }
        reverse(in+1,in+1+li);
    }
    inline void initrmq() {
        for(int i=1;i<sal;i++) rmq[i][0] = h[i];
        for(int j=1;j<=Log[sal];j++) for(int i=1;i<sal;i++) rmq[i][j] = min( rmq[i][j-1] , rmq[i+(1<<(j-1))][j-1] );
    }
    inline int query(int l,int r) {
        l = rnk[l] , r = rnk[r];
        if( l > r ) swap(l,r);
        --r;
        int L = Log[r-l+1];
        return min( rmq[l][L] , rmq[r-(1<<L)+1][L] );
    }
    inline void work(char* in,int li) {
        for(int i=1;i<=li;i++) extend(in[i]-'a',li-i+1);
        pre(1) , dfs(1);
        in[li+1] = '#' , geth(in,li) , initrmq();
    }
}prf,suf;

inline int lcp(int i,int j) {
    return prf.query(i,j);
}
inline int lcs(int i,int j) {
    return suf.query(li-j+1,li-i+1);
}
inline void calc(int len) {
    for(int st=1,sst,lc;st+len<=li;st+=len) {
        sst = st + len , lc = lcp(st,sst) + lcs(st-1,sst-1);
        if( lc >= len ) {
            ans = max( ans , len * 2 );
        }
    }
}

int main() {
    scanf("%s",in+1) , li = strlen(in+1);
    for(int i=2;i<=li;i++) Log[i] = Log[i>>1] + 1;
    suf.work(in,li) , reverse(in+1,in+1+li) , prf.work(in,li) , reverse(in+1,in+1+li);
    for(int i=1;i<=li;i++) calc(i);
    printf("%d\n",ans);
    return 0;
}

倍增:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define debug cout
using namespace std;
const int maxn=2e6+1e2,maxl=23;

char in[maxn>>1];
int Log[maxn>>1],li,ans;

struct SuffixArray  {
    int sa[maxn],rnk[maxn],h[maxn],tax[maxn],tp[maxn],rmq[maxn][maxl],n,m;
    inline void Resort() {
        for(int i=0;i<=m;i++) tax[i] = 0;
        for(int i=1;i<=n;i++) tax[rnk[i]]++;
        for(int i=1;i<=m;i++) tax[i] += tax[i-1];
        for(int i=n;i;i--) sa[tax[rnk[tp[i]]]--] = tp[i];
    }
    inline bool judge(int* s,int a,int b,int l) {
        return s[a] == s[b] && s[a+l] == s[b+l];
    }
    inline void buildh() {
        for(int i=1,k=0,j;i<=n;i++) {
            k = k ? k - 1 : 0 , j = sa[rnk[i]-1];
            while( in[i+k] == in[j+k] ) ++k;
            h[rnk[i]-1] = k;
        }
    }
    inline void get(char* in,int nn) {
        n = nn;
        for(int i=1;i<=n;i++) rnk[i] = in[i] , tp[i] = i;
        m = 127 , Resort();
        for(int w=1,p=1;p<n;w+=w,m=p) {
            p = 0;
            for(int i=n-w+1;i<=n;i++) tp[++p] = i;
            for(int i=1;i<=n;i++) if( sa[i] > w ) tp[++p] = sa[i] - w;
            Resort(); swap(tp,rnk); rnk[sa[1]] = p = 1;
            for(int i=2;i<=n;i++)
                rnk[sa[i]] = judge(tp,sa[i],sa[i-1],w) ? p : ++p;
        }
        buildh() , initrmq();
    }
    inline void initrmq() {
        for(int i=1;i<n;i++) rmq[i][0] = h[i];
        for(int j=1;j<=Log[n];j++) for(int i=1;i<n;i++) rmq[i][j] = min( rmq[i][j-1] , rmq[i+(1<<(j-1))][j-1] );
    }
    inline int query(int l,int r) {
        l = rnk[l] , r = rnk[r];
        if( l > r ) swap(l,r);
        --r;
        int L = Log[r-l+1];
        return min( rmq[l][L] , rmq[r-(1<<L)+1][L] );
    }
}prf,suf;

inline int lcp(int i,int j) {
    return prf.query(i,j);
}
inline int lcs(int i,int j) {
    return suf.query(li-j+1,li-i+1);
}
inline void calc(int len) {
    for(int st=1,sst,lc;st+len<=li;st+=len) {
        sst = st + len , lc = lcp(st,sst) + lcs(st-1,sst-1);
        if( lc >= len ) {
            ans = max( ans , len * 2 );
        }
    }
}

int main() {
    scanf("%s",in+1) , li = strlen(in+1);
    for(int i=2;i<=li;i++) Log[i] = Log[i>>1] + 1;
    prf.get(in,li) , reverse(in+1,in+1+li) , suf.get(in,li);
    for(int i=1;i<=li;i++) calc(i);
    printf("%d\n",ans);
    return 0;
}

Update 20180509:
然而现在我还不会倍增......
不过我可以后缀平衡树求后缀数组是吧。复杂度也是nlogn。
由于这题测试点1718的特殊性，后缀平衡树的log跑不满，可以随便AC。
而测试点24也能过，只有25跑2s+......
代码:

#pragma GCC optimize("Ofast")
#pragma GCC optimize("no-stack-protector")
#pragma GCC target("avx")
#include<cstdio>
#include<cstring>
#include<algorithm>
const int maxn=1e6+1e2,maxl=23;
const double alpha=0.95;

char in[maxn];
int Log[maxn],li,ans;

struct SuffixArray  {
    int sa[maxn],rnk[maxn],h[maxn],rmq[maxn][maxl],n,m,sal;
    
    int at[maxn],lson[maxn],rson[maxn],siz[maxn],sf[maxn],root,cnt;
    int seq[maxn],sql;
    int fail,failfa;
    double v[maxn],vfl,vfr;
    
    inline bool cmp(int x,int y) {
        if( !x || !y ) return !x;
        if( in[x] != in[y] ) return in[x] < in[y];
        else return v[at[x-1]] < v[at[y-1]];
    }
    inline void upgrade(int pos,double l,double r) {
        siz[pos] = siz[lson[pos]] + siz[rson[pos]] + 1;
        if( std::max( siz[lson[pos]] , siz[rson[pos]] ) > siz[pos] * alpha ) fail = pos , failfa = -1 , vfl = l , vfr = r;
        else if( fail == lson[pos] || fail == rson[pos] ) failfa = pos;
    }
    inline void insert(int &pos,double l,double r,const int &id) {
        if( !pos ) {
            v[at[id]=pos=++cnt]= ( l + r ) / 2.0 , siz[pos] = 1 , sf[pos] = id;
            return;
        } const double vmid = ( l + r ) / 2.0;
        if( cmp(sf[pos],id) ) insert(rson[pos],vmid,r,id) , upgrade(pos,l,r); // id > sf[pos] .
        else insert(lson[pos],l,vmid,id) , upgrade(pos,l,r);
    }
    inline int rebuild(int ll,int rr,double l,double r) {
        const int mid = ( ll + rr ) >> 1 , pos = seq[mid];
        const double vmid = ( l + r ) / 2.0; v[pos] = vmid , siz[pos] = rr - ll + 1;
        if( ll < mid ) lson[pos] = rebuild(ll,mid-1,l,vmid);
        if( mid < rr ) rson[pos] = rebuild(mid+1,rr,vmid,r);
        return pos;
    }
    inline void dfs(int pos) {
        if(lson[pos]) dfs(lson[pos]);
        seq[++sql] = pos;
        if(rson[pos]) dfs(rson[pos]);
        lson[pos] = rson[pos] = siz[pos] = 0;
    }
    inline void insert(const int &id) {
        fail = 0 , failfa = -1 , insert(root,0,1,id);
        if(fail) {
            sql = 0 , dfs(fail);
            if( ~failfa ) {
                if( fail == lson[failfa] ) lson[failfa] = rebuild(1,sql,vfl,vfr);
                else rson[failfa] = rebuild(1,sql,vfl,vfr);
            } else root = rebuild(1,sql,0,1);
        }
    }
    inline void getsa(int pos) {
        if(lson[pos]) getsa(lson[pos]);
        sa[++sal] = n - sf[pos] + 1;
        if(rson[pos]) getsa(rson[pos]);
    }
    
    inline void work(char* in,int li) {
        n = li , std::reverse(in+1,in+1+n) , in[n+1] = '#';
        insert(0);
        for(int i=1;i<=li;i++) insert(i);
        getsa(root) , std::reverse(in+1,in+1+n) , geth() , initrmq();
    }
    
    inline void geth() {
        for(int i=1;i<=n;i++) rnk[sa[i]] =i;
        for(int i=1,k=0,j;i<=n;i++) {
            k = k ? k - 1 : 0 , j = sa[rnk[i]-1];
            while( in[i+k] == in[j+k] ) ++k;
            h[rnk[i]-1] = k;
        }
    }
    inline void initrmq() {
        for(int i=1;i<n;i++) rmq[i][0] = h[i];
        for(int j=1;j<=Log[n];j++) for(int i=1;i+(1<<(j-1))<=n;i++) rmq[i][j] = std::min( rmq[i][j-1] , rmq[i+(1<<(j-1))][j-1] );
    }
    inline int query(int l,int r) {
        l = rnk[l] , r = rnk[r];
        if( l > r ) std::swap(l,r);
        --r;
        int L = Log[r-l+1];
        return std::min( rmq[l][L] , rmq[r-(1<<L)+1][L] );
    }
}prf,suf;

inline int lcp(int i,int j) {
    return prf.query(i,j);
}
inline int lcs(int i,int j) {
    return suf.query(li-j+1,li-i+1);
}
inline void calc(int len) {
    for(int st=1,sst,lc;st+len<=li&&!ans;st+=len) {
        sst = st + len , lc = lcp(st,sst) + lcs(st-1,sst-1);
        if( lc >= len ) ans = len * 2;
    }
}

int main() {
    fread(in+1,1,maxn,stdin) , li = strlen(in+1);
    for(int i=2;i<=li;i++) Log[i] = Log[i>>1] + 1;
    prf.work(in,li) , std::reverse(in+1,in+1+li) , suf.work(in,li);
    for(int i=li;i&&!ans;i--) calc(i);
    printf("%d\n",ans);
    return 0;
}

 

T3:

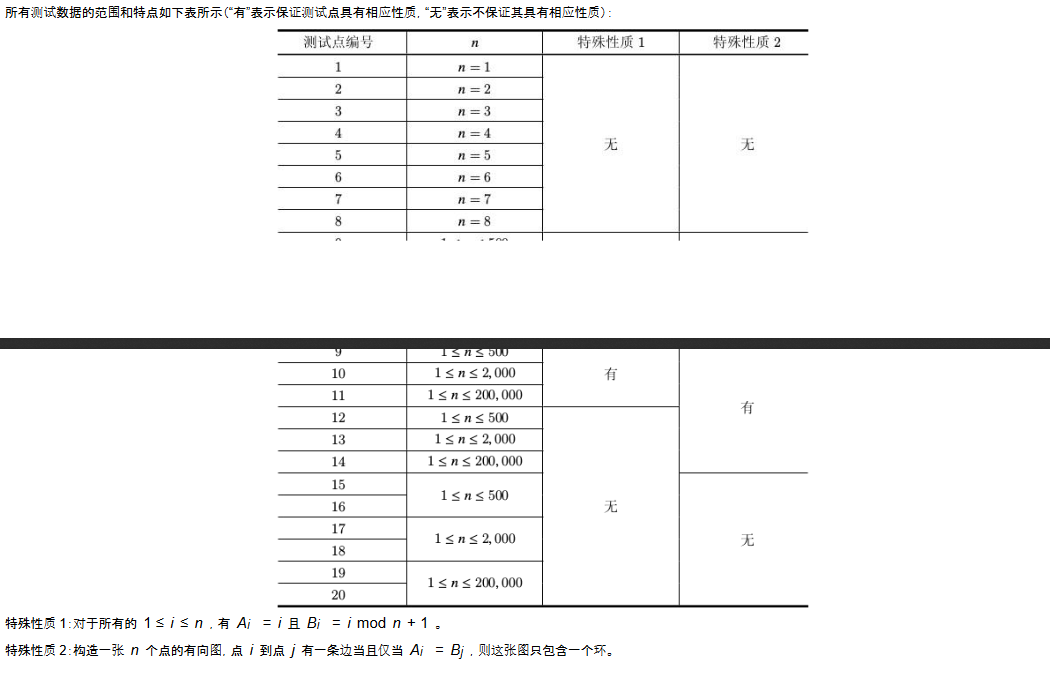
考试的时候根本没时间看这题了(其实是前两题不会就心态爆炸弃疗了)。
正解是一个神奇的构造:

代码:

#include<cstdio>
#include<algorithm>
const int maxn=2e5+1e2;

int a[maxn],b[maxn],sou[maxn],tar[maxn],swa[maxn][2],swb[maxn][2],n,al,bl;

int main() {
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",a+i) , sou[a[i]] = i;
    for(int i=1;i<=n;i++) scanf("%d",b+i) , tar[b[i]] = i;
    for(int i=1,t;i<=n;i++) if( a[i] != b[i] ) {
        if( tar[a[i]] >= sou[b[i]] ) std::swap(a[i],a[t=sou[b[i]]]) , sou[a[t]] = t , sou[a[i]] = i , swa[++al][0] = i , swa[al][1] = t;
        else std::swap(b[i],b[t=tar[a[i]]]) , tar[b[t]] = t , tar[b[i]] = i , swb[++bl][0] = i , swb[bl][1] = t;
    }
    printf("%d\n",al+bl);
    for(int i=1;i<=al;i++) printf("%d %d\n",swa[i][0],swa[i][1]);
    for(int i=bl;i;i--) printf("%d %d\n",swb[i][0],swb[i][1]);
    return 0;
}

我は此処にて石となる 同胞を護る石となる
我愿在此成为一块石 成为保护兄弟姐妹的石头
宜災いを受けてなお 物言わぬ石に在うべし
诚然地承受灾难 一言不发的石头
この災厄に触れたとて 失うがこそ卑しけれ
以体验这灾祸为荣 以错过此为耻
心より憎むものなれど 母の手に似た慰撫に泣く
虽然你从心里憎恨我 但我会用如同母亲般的手抚慰并为你流泪

我は此処にて石となる 幾千の時刻を越えた先
我愿在此成为一块石 成为历经数千年的石头
共に手をとり生きようと その顔を焼き付けて
在那脸上烙上[一起手牵手活下去吧]
呪われた血を今日は泣く 失うがこそ悲しいけれ
今天流下被诅咒的血泪 错过了才是悲伤
愛し愛されたいと哭く 鬼の姿に人の夢
为想爱与被爱而哭 化身鬼魂现于人梦