5312: 冒险 线段树 复杂度分析
国际惯例的题面: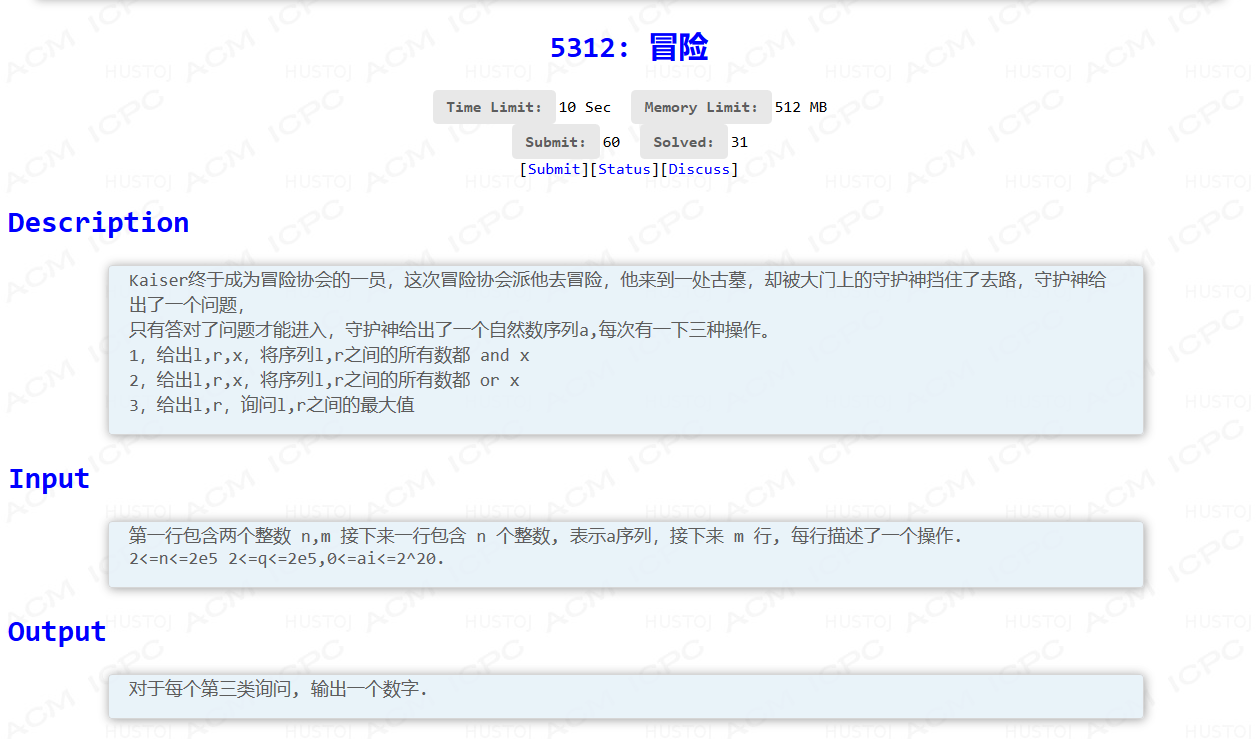
一看到这种维护序列的题,数据范围分块过不去,显然线段树了。
考虑位运算的性质,and相当于钦定一些位必须是0,or相当于钦定一些位必须是1,这都是一些区间赋值操作。
然而我们不可以按位确定,为什么?因为当你确定了最高位之后,你需要在满足高位的情况下求出低位,这相当于是一个取子集操作,单层的树是不可做的。(树套树20层?恭喜你不如n^2暴力了)
于是去ORZ了英文题解,发现他是这样分析的:
我们对每一个位上的操作把数分成两类,有影响的和无影响的。因为操作对这两种数不同,所以我们不能直接维护。
但是,显然在一个操作之后,两种不同的数会被变得相同!
于是,当我们操作到某一个区间,如果这个操作对区间内的所有数并不是全部相同,那么我们递归下去做(也就是访问多余节点)。因为操作后两边这些位的数会变得相同,而变相同的次数有限,所以复杂度是正确的。(表示原文一堆势能分析不明觉厉)
然后就是怎么判断操作对某个区间是否相同的问题了。我们维护区间的and和和or和,显然两者的xor和就是这个区间存在不同的位。如果这些存在不同的位与本次操作会被钦定的位and起来不为0的话,就说明这次操作对这个区间的所有数并非完全相同,需要递归下去做。
另外,这题略卡常......
代码:

1 #pragma GCC optimize(2) 2 #include<cstdio> 3 #include<algorithm> 4 #include<cctype> 5 const unsigned maxn=2e5+1e2,maxe=(maxn<<2)+5; 6 const unsigned full = ( 1 << 21 ) - 1; 7 8 unsigned in[maxn]; 9 struct SegmentTree { 10 unsigned andsu[maxe],orsu[maxe],lazyand[maxe],lazyor[maxe],mx[maxe]; 11 #define lson(pos) (pos<<1) 12 #define rson(pos) (pos<<1|1) 13 inline void upgrade(unsigned pos) { 14 andsu[pos] = andsu[lson(pos)] & andsu[rson(pos)] , orsu[pos] = orsu[lson(pos)] | orsu[rson(pos)] , mx[pos] = std::max( mx[lson(pos)] , mx[rson(pos)] ); 15 } 16 inline void build(unsigned pos,unsigned ll,unsigned rr) { 17 lazyand[pos] = full; 18 if( ll == rr ) return void( andsu[pos] = orsu[pos] = mx[pos] = in[ll] ); 19 const unsigned mid = ( ll + rr ) >> 1; 20 build(lson(pos),ll,mid) , build(rson(pos),mid+1,rr) , upgrade(pos); 21 } 22 inline void apply(unsigned pos,const unsigned &x,const unsigned &tpe) { // tpe = 1 means and , tpe = 2 means or . 23 if( tpe == 1 ) andsu[pos] &= x , orsu[pos] &= x , lazyand[pos] &= x , lazyor[pos] &= x , mx[pos] &= x; 24 else if( tpe == 2 ) andsu[pos] |= x , orsu[pos] |= x , lazyor[pos] |= x , mx[pos] |= x; 25 } 26 inline void push(unsigned pos) { 27 if( lazyand[pos] != full ) apply(lson(pos),lazyand[pos],1) , apply(rson(pos),lazyand[pos],1) , lazyand[pos] = full; 28 if( lazyor ) apply(lson(pos),lazyor[pos],2) , apply(rson(pos),lazyor[pos],2) , lazyor[pos] = 0; 29 } 30 inline bool allsame(unsigned pos,const unsigned &x,const unsigned &tpe) { 31 unsigned dif = andsu[pos] ^ orsu[pos] , ref = ( tpe == 1 ? 0 : full ) ^ x; 32 return ! ( dif & ref ); 33 } 34 inline void update(unsigned pos,unsigned l,unsigned r,const unsigned &ll,const unsigned &rr,const unsigned &x,const unsigned &tpe) { 35 if( ll <= l && r <= rr && allsame(pos,x,tpe) ) return apply(pos,x,tpe); 36 push(pos); const unsigned mid = ( l + r ) >> 1; 37 if( rr <= mid ) update(lson(pos),l,mid,ll,rr,x,tpe); 38 else if( ll > mid ) update(rson(pos),mid+1,r,ll,rr,x,tpe); 39 else update(lson(pos),l,mid,ll,rr,x,tpe) , update(rson(pos),mid+1,r,ll,rr,x,tpe); 40 upgrade(pos); 41 } 42 inline unsigned query(unsigned pos,unsigned l,unsigned r,const unsigned &ll,const unsigned &rr) { 43 if( ll <= l && r <= rr ) return mx[pos]; 44 push(pos); const unsigned mid = ( l + r ) >> 1; 45 if( rr <= mid ) return query(lson(pos),l,mid,ll,rr); 46 else if( ll > mid ) return query(rson(pos),mid+1,r,ll,rr); 47 return std::max( query(lson(pos),l,mid,ll,rr) , query(rson(pos),mid+1,r,ll,rr) ); 48 } 49 }sgt; 50 51 inline char nextchar() { 52 static const unsigned BS = 1 << 22; 53 static unsigned char buf[BS],*st=buf+BS,*ed=st; 54 if( st == ed ) ed = buf + fread(st=buf,1,BS,stdin); 55 return st == ed ? -1 : *st++; 56 } 57 inline unsigned getint() { 58 unsigned ret = 0 , ch; 59 while( !isdigit(ch=nextchar()) ); 60 do ret=ret*10+ch-'0'; while( isdigit(ch=nextchar()) ); 61 return ret; 62 } 63 64 int main() { 65 static unsigned n,m; 66 n = getint() , m = getint(); for(unsigned i=1;i<=n;in[i++]=getint()); 67 sgt.build(1,1,n); 68 for(unsigned i=1,o,l,r,x;i<=m;i++) o = getint() , l = getint() , r = getint() , o == 3 ? printf("%d\n",sgt.query(1,1,n,l,r)) : x = getint() , sgt.update(1,1,n,l,r,x,o); 69 return 0; 70 }
はらり はらり さやかな白よ
飘零的 飞散的 明亮的白色啊
夢の 終わる その場所で
在这里 梦的终结之所
淡く 流れ わたしの恋を
淡淡地 流淌的 我的爱恋
こころ ふかく そめてゆく
深深地 染进心中



 浙公网安备 33010602011771号
浙公网安备 33010602011771号