Bzoj2673 3961: [WF2011]Chips Challenge 费用流
国际惯例题面: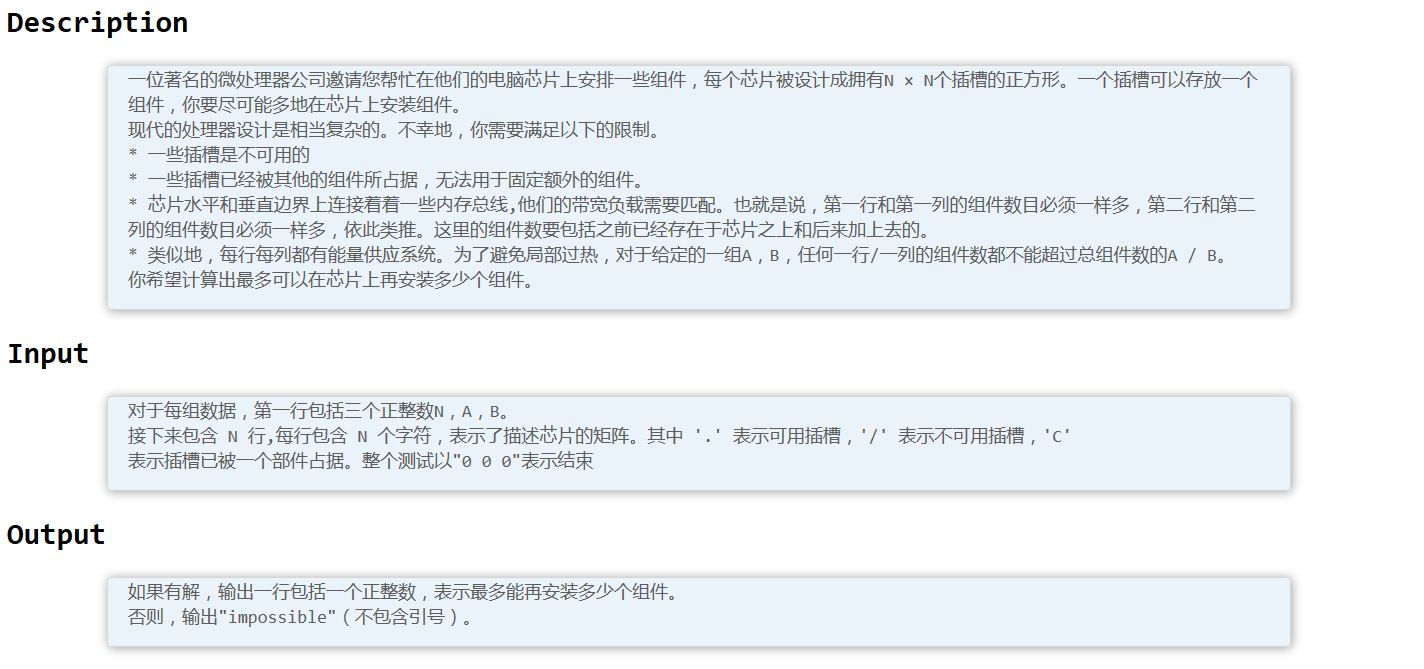
如果我们枚举放几个零件的话,第二个限制很容易解决,但是第一个怎么办?(好的,这么建图不可做)
考虑我们枚举每行每列最多放几个零件t,然后计算零件总数sum。这样如果可行的话,则有t*B<=sum*A。
考虑第一个限制怎么办。我们可以钦定所有可行的位置都放上零件,然后再把多的零件拆下来。
我们令sxi为第i行能放的最多零件数,syi为第i列能放的最多零件数。
由源点向每一行连流量sxi费用0的边,每一列向汇点连流量syi费用0的边。
然后让每一行i向每一列i连流量t费用0的边,表示第i行和第j列最多同时不拆(留下)t个零件。
最后对于所有输入为'.'的格子ij,由第i行向第j列连容量1费用1的边,表示拆下第i行第j列的零件。
跑费用流,必须满流才满足题意(零件要么行和列同时留下,要么拆掉),费用表示拆掉的零件个数。
然后用留下的零件个数和t去比较是否合法,计算答案就行了。
感觉这题就是给了我们一种网络流建图,补集转化的姿势(如果选择的流量行列不移动统一,那么去掉的流量是否统一?如果选择的不好限制,去掉的是否容易限制?)
代码:

1 #pragma GCC optimize(2) 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<queue> 6 const int maxn=1e2+1e1,maxe=maxn*maxn; 7 const int inf=0x3f3f3f3f; 8 9 char in[maxn][maxn]; 10 int s[maxn],t[maxe<<3],nxt[maxe<<3],f[maxe<<3],c[maxe<<3],cnt; 11 int dis[maxn],inq[maxn],ins[maxn],st,ed,cst; 12 int sx[maxn],sy[maxn],su,ini; 13 int n,A,B,ans; 14 15 inline void coredge(int from,int to,int flow,int cost) { 16 t[++cnt] = to , f[cnt] = flow , c[cnt] = cost , 17 nxt[cnt] = s[from] , s[from] = cnt; 18 } 19 inline void singledge(int from,int to,int flow,int cost) { 20 coredge(from,to,flow,cost) , coredge(to,from,0,-cost); 21 } 22 inline bool spfa() { 23 memset(dis,0x3f,sizeof(dis)) , dis[st] = 0; 24 std::queue<int> q; q.push(st) , inq[st] = 1; 25 while( q.size() ) { 26 const int pos = q.front(); q.pop() , inq[pos] = 0; 27 for(int at=s[pos];at;at=nxt[at]) 28 if( f[at] && dis[t[at]] > dis[pos] + c[at] ) { 29 dis[t[at]] = dis[pos] + c[at]; 30 if( !inq[t[at]] ) q.push(t[at]) , inq[t[at]] = 1; 31 } 32 } 33 return dis[ed] != inf; 34 } 35 inline int dfs(int pos,int flow) { 36 if( pos == ed ) return flow; 37 int ret = 0 , now = 0; ins[pos] = 1; 38 for(int at=s[pos];at;at=nxt[at]) 39 if( f[at] && !ins[t[at]] && dis[t[at]] == dis[pos] + c[at] ) { 40 now = dfs(t[at],std::min(flow,f[at])) , 41 ret += now , flow -= now , cst += c[at] * now , 42 f[at] -= now , f[at^1] += now; 43 if( !flow ) return ins[pos] = 0 , ret; 44 } 45 if( !ret ) dis[pos] = inf; 46 return ins[pos] = 0 , ret; 47 } 48 inline int flow() { // we must got full flow . 49 int ret = 0 , now = 0; 50 while( spfa() ) while( ( now = dfs(st,inf) ) ) ret += now; 51 return ret; 52 } 53 54 inline void build(int t) { 55 memset(s,0,sizeof(s)) , cnt = 1 , st = n * 2 + 1 , ed = st + 1 , cst = 0; 56 #define cov(x,id) (x*2-1+id) 57 for(int i=1;i<=n;i++) { 58 singledge(st,cov(i,0),sx[i],0) , 59 singledge(cov(i,0),cov(i,1),t,0) , 60 singledge(cov(i,1),ed,sy[i],0) ; 61 } 62 for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if( in[i][j] == '.' ) singledge(cov(i,0),cov(j,1),1,1); 63 } 64 inline int calc(int t) { 65 build(t); 66 if( flow() != su ) return -1; // illegal . 67 int used = su - cst; 68 return used * A >= t * B ? used - ini : -1; 69 } 70 71 int main() { 72 static int cse; 73 while( scanf("%d%d%d",&n,&A,&B) == 3 && ( n || A || B ) ) { 74 memset(sx,0,sizeof(sx)) , memset(sy,0,sizeof(sy)) , ini = su = 0 , ans = -1; 75 for(int i=1;i<=n;i++) { 76 scanf("%s",in[i]+1); 77 for(int j=1;j<=n;j++){ 78 if( in[i][j] != '/' ) ++sx[i] , ++sy[j] , ++su; 79 ini += in[i][j] == 'C'; 80 } 81 } 82 for(int i=0;i<=n;i++) ans = std::max( ans , calc(i) ); 83 printf("Case %d: ",++cse); 84 if( !~ans ) puts("impossible"); 85 else printf("%d\n",ans); 86 } 87 return 0; 88 }
(话说我都多路增广+码内O2了才卡到332MS,那几个几十MS过掉的是怎么做到的)
華やかな 煌びやかな運命を
做着拥有绚烂命运的梦
夢見て 泣いた夜は
却因为这样的梦 止不住泪水
银色の流星も泣いている
银色的流星也在哭泣
ナツシスに向けて
向着水仙花海
あっけなく さよならを告げぬよう
不想轻易说出再见
唇が 告げぬように
所以咬紧双唇
呟きに星空も木霊する
唯有轻声细语回响在星空下
ナツシスに向けて
朝着水仙
いつまでも届け
将它传递到永远



 浙公网安备 33010602011771号
浙公网安备 33010602011771号