4951: [Wf2017]Money for Nothing 决策单调性 分治
Bzoj4951:决策单调性 分治
国际惯例题面: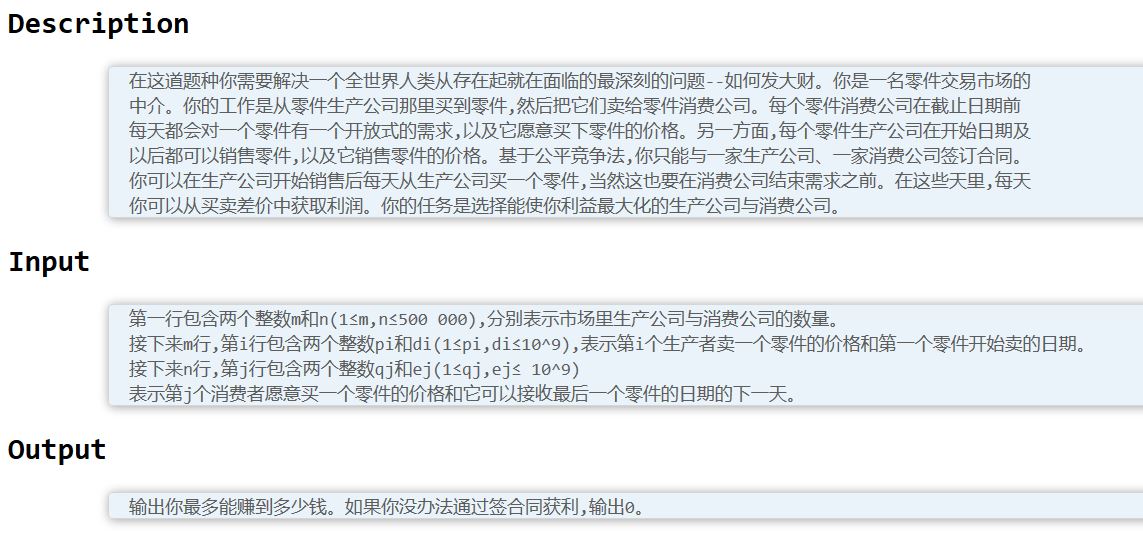
一句话题面:
供应商出货日期为Ei,售价为Pi;用户收购截止日期为Si,收购价格为Gi。我们要求max((Si-Ej)*(Gi-Pj))。
显然如果我们把这两者都按照Ei,Si递增排序,则Pi,Gi都是单调降的。
为什么?如果一个供应商生产时间后且价格高,显然你不会选择他;如果一个用户购买时间短且收购价格低,显然你也不会选择他。
然后我们会写n^2暴力了。考虑优化。
这种DP要么斜率+数据结构优化,要么就是决策单调性。
考虑斜率优化,发现这是一个三维凸包问题,不会做。
考虑决策单调性,我们猜想,对于Si递增的用户,采用的最有供货商的Ei也是单调增的。
如何证明,考虑反证法。
我们假设两个供货商出货日期为E1,E2,价格为P1,P2。
两个用户截止日期为S1,S2,收购价格为G1,G2。
不妨令E1<E2,P1>P2且S1<S2,G1>G2。
如果不满足决策单调性,我们有:
(E1-S2)*(P1-G2)>(E1-S1)*(P1-G1)
(E2-S1)*(P2-G1)>(E2-S1)*(P2-G2)
整理得:
S2*G2-S1*G1>P1*(S2-S1)+E1*(G2-G1)
P2*(S2-S1)+E2*(G2-G1)>S2*G2-S1*G1
根据不等号的传递性,我们有:
P2*(S2-S1)+E2*(G2-G1)>P1*(S2-S1)+E1*(G2-G1)
整理得:
(E2-E1)*(G2-G1)>(S2-S1)*(P1-P2)
根据我们的前提条件,E2-E1>0,G2-G1<0,S2-S1>0,P1-P2>0。
这样的话,左式((E2-E1)*(G2-G1))<0,右式((S2-S1)*(P1-P2))>0。
显然一个<0的数大于一个>0的数是不可能的,所以假设不成立,原结论成立,决策单调性得证。
然后就是代码实现的问题了,我用的是经典的分治写法,就是对于每一个用户区间的中点,找到最优供货商,然后再分离区间递归计算。
注意如果乘法的时候两边都是负数,我们应该特判掉并返回-inf(因为这个状态不合法,不能更新答案),但是只有一边是负数的时候,我们应该计算出他的值(虽然这个状态不能更新答案,但是这个状态能更新决策)。
我一开始看到<0就返回-inf,WA了不知道多少发,身败名裂。
代码:

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 typedef long long int lli; 5 const int maxn=5e5+1e2; 6 const lli inf=0x3f3f3f3f3f3f3f3fll; 7 8 struct Point { 9 int x,y; 10 friend bool operator < (const Point &a,const Point &b) { 11 return a.x != b.x ? a.x < b.x : a.y < b.y; 12 } 13 }pro[maxn],usr[maxn]; 14 15 inline int fix(Point* dst,int len,bool tpe) { // tpe = 0 solve provider by pushing stack , cmp = 1 solve user by poping stack . 16 static Point stk[maxn]; 17 std::sort(dst+1,dst+1+len); 18 int top = 0; 19 if( !tpe ) { 20 for(int i=1;i<=len;i++) if( !top || stk[top].y > dst[i].y ) stk[++top] = dst[i]; 21 } else { 22 for(int i=1;i<=len;i++) { 23 while( top && stk[top].y <= dst[i].y ) --top; 24 stk[++top] = dst[i]; 25 } 26 } 27 memcpy(dst+1,stk+1,sizeof(Point)*top); 28 return top; 29 } 30 31 lli ans; 32 33 inline lli calc(const Point &pro,const Point &usr) { 34 if( usr.x < pro.x && usr.y < pro.y ) return -inf; 35 return (lli) ( usr.x - pro.x ) * ( usr.y - pro.y ); 36 } 37 inline void solve(int pl,int pr,int ul,int ur) { 38 if( pl == pr || ul == ur ) { 39 for(int i=pl;i<=pr;i++) for(int j=ul;j<=ur;j++) ans = std::max( ans , calc(pro[i],usr[j]) ); 40 return; 41 } 42 int pmid = pl , umid = ( ul + ur ) >> 1; 43 lli cur = -inf, cal; 44 for(int i=pl;i<=pr;i++) 45 if( ( cal = calc(pro[i],usr[umid]) ) > cur ) cur = cal , pmid = i; 46 ans = std::max( ans , cur ); 47 if( ul < umid ) solve(pl,pmid,ul,umid-1); 48 if( umid < ur ) solve(pmid,pr,umid+1,ur); 49 } 50 51 int main() { 52 static int n,m; 53 scanf("%d%d",&n,&m); 54 for(int i=1;i<=n;i++) scanf("%d%d",&pro[i].x,&pro[i].y); 55 for(int i=1;i<=m;i++) scanf("%d%d",&usr[i].x,&usr[i].y); 56 n = fix(pro,n,0) , m = fix(usr,m,1); 57 solve(1,n,1,m) , printf("%lld\n",ans); 58 return 0; 59 }
作为业界良心的我还是附送官方数据吧(Lemon格式打包):
链接:https://pan.baidu.com/s/1jbjZ6OvS5Wf5Ls46nvrRNg 密码:434d
祈る事を諦めた
我已经放弃了向神祈祷
透き通る空の朝
在那透明澄澈的清晨中
どんな気持ち抱えてても
无论怀抱着怎样的心绪
誰にも届かないなんて
也完全无法向他人传递
まるで私はエコー
仿佛只是自身在不断回响



 浙公网安备 33010602011771号
浙公网安备 33010602011771号