20180329小测

让大家都AK的信心赛......
话说这种考试有什么意思(不)，还不如做我出的那套模拟题呢......

T1:

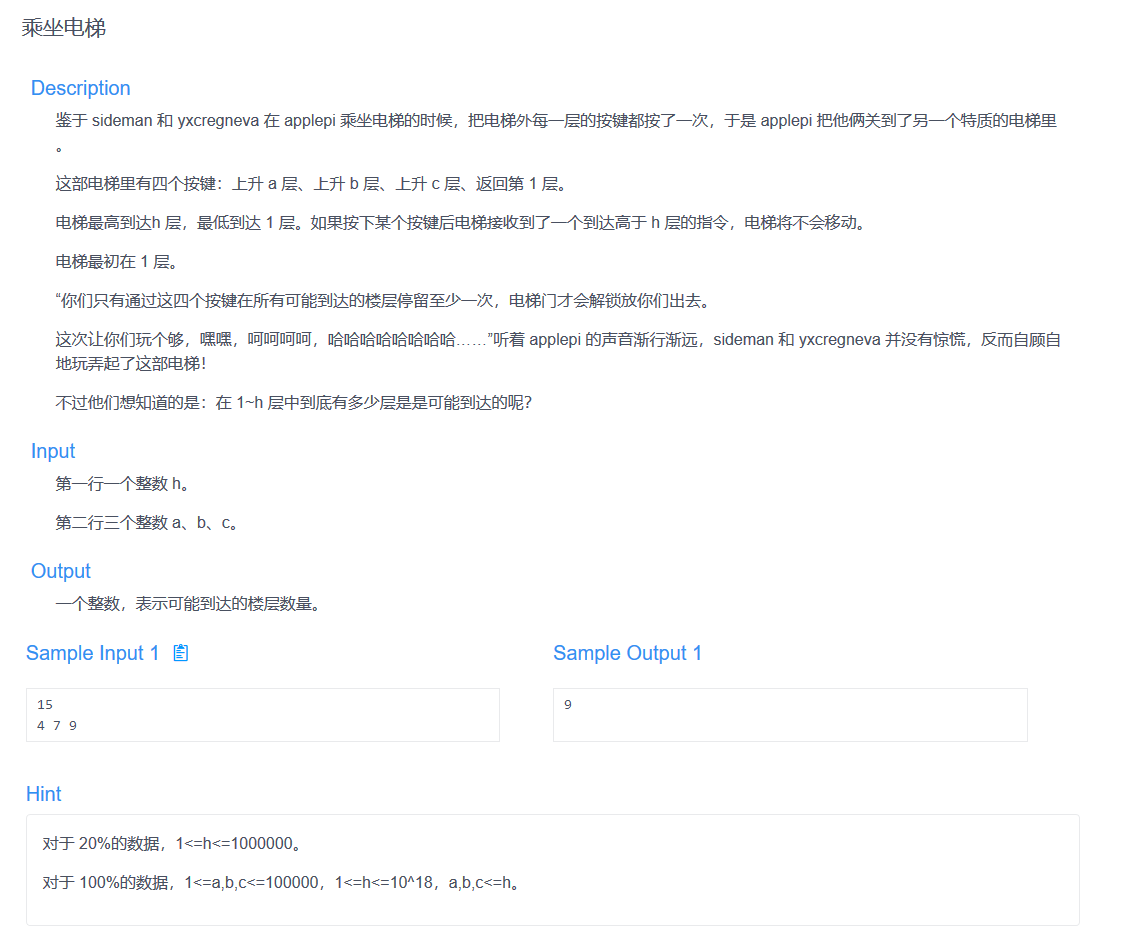
其实这题是我三道题里AC得最晚的......
首先我们能用bitset+大力背包骗到58-64分......
考虑我们如果先枚举两个数能组合出的值，再计算另外一个数的方案数，什么情况下会算重?
显然是当这个值取模最后的那个数相同的时候，这样一个方案数会被计算多次!
此外还有一个十分显然的结论:当两个值取模最后那个数相同时，较大的那个值的答案会被包含在较小的那个值的答里面。
这样的话，我们在取模abc中某一个数的同余系下跑一个最短路，用另外两个数做边进行转移，最后再统计一发答案不就好了。
60分bitset代码:

#pragma GCC optimize(3)
#include<cstdio>
#include<bitset>
const int maxn=1e8+1e2;
std::bitset<maxn> vis;

long long h;
int a,b,c,ans;


int main() {
    scanf("%lld%d%d%d",&h,&a,&b,&c);
    if( a == 1 || b == 1 || c == 1 ) return printf("%lld\n",h),0;
    for(int i=0;a*i<h;i++) {
        if( vis[a*i] ) break;
        for(int j=0;a*i+b*j<h;j++) {
            if( vis[a*i+b*j] ) break;
            for(int k=0;a*i+b*j+k*c<h;k++) {
                if( vis[a*i+b*j+k*c] ) break;
                vis[a*i+b*j+k*c] = 1;
            }
        }
    }
    printf("%llu\n",vis.count());
    return 0;
}

正解代码:

#include<bits/stdc++.h>
#define bool unsigned char
typedef long long int lli;
using namespace std;
const int maxn=1e5+1e2;

lli h,ans;
lli dis[maxn];
int s[maxn],t[maxn<<4],nxt[maxn<<4],l[maxn<<4];
bool inq[maxn];
int a,b,c;

inline void addedge(int from,int to,int len) {
    static int cnt = 0;
    t[++cnt] = to , l[cnt] = len ,
    nxt[cnt] = s[from] , s[from] = cnt;
}
inline void spfa(int st) {
    memset(dis,0x7f,sizeof(dis)) , dis[st] = 0;
    queue<int> q; q.push(st) , inq[st] = 1;
    while( q.size() ) {
        const int pos = q.front(); q.pop() , inq[pos] = 0;
        for(int at=s[pos];at;at=nxt[at])
            if( dis[t[at]] > dis[pos] + l[at] ) {
                dis[t[at]] = dis[pos] + l[at];
                if( !inq[t[at]] ) q.push(t[at]) , inq[t[at]] = 1;
            }
    }
}
inline void getans() {
    --h;
    for(int i=0;i<c;i++)
        if( dis[i] <= h )
            ans += ( h - dis[i] ) / c + 1;
}

int main() {
    scanf("%lld%d%d%d",&h,&a,&b,&c);
    if( a > b ) swap(a,b);
    if( b > c ) swap(b,c);
    for(int i=0;i<c;i++)
        addedge(i,(i+a)%c,a) , addedge(i,(i+b)%c,b);
    spfa(0);
    getans();
    printf("%lld\n",ans);
    return 0;
}

 

T2:

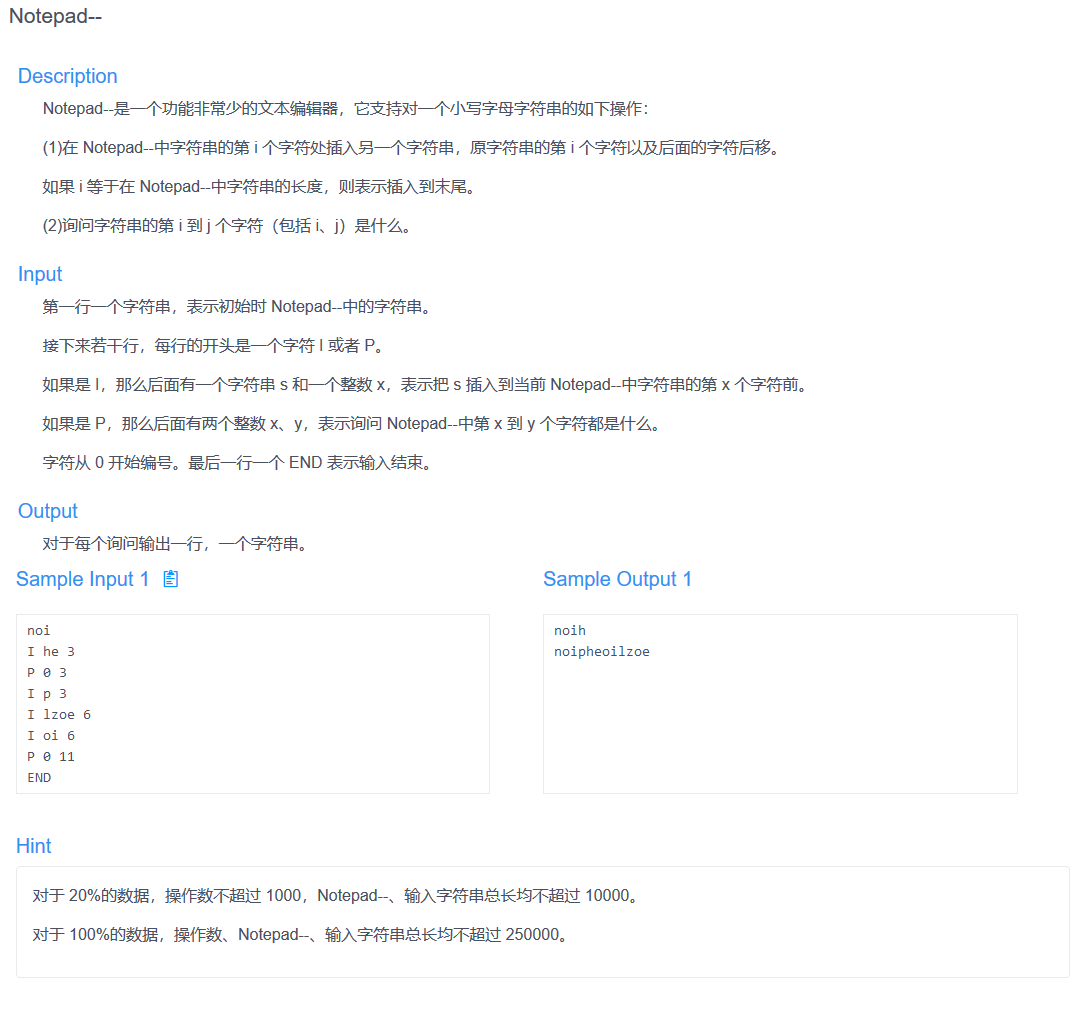
怕不是stl:rope裸题......
rope能实现区间提取，单点插入区间，正好能用来做这道题......
代码:

#include<iostream>
#include<ext/rope>
const int maxn=2.5e5+1e2;

char in[maxn];
__gnu_cxx::rope<char> str,ans;

int main() {
    static char com[10];
    static int k,len;
    std::ios::sync_with_stdio(0) , std::cin.tie(0) , std::cout.tie(0);
    std::cin >> in , str = in;
    while( ( std::cin >> com ) && *com != 'E' ) {
        if( *com == 'I' ) {
            std::cin >> in >> k;
            str.insert(k,in);
        } else if( *com == 'P' ) {
            std::cin >> k >> len;
            ans = str.substr(k,len-k+1);
            std::cout << ans << std::endl;
        }
    }
    return 0;
}

 

T3:

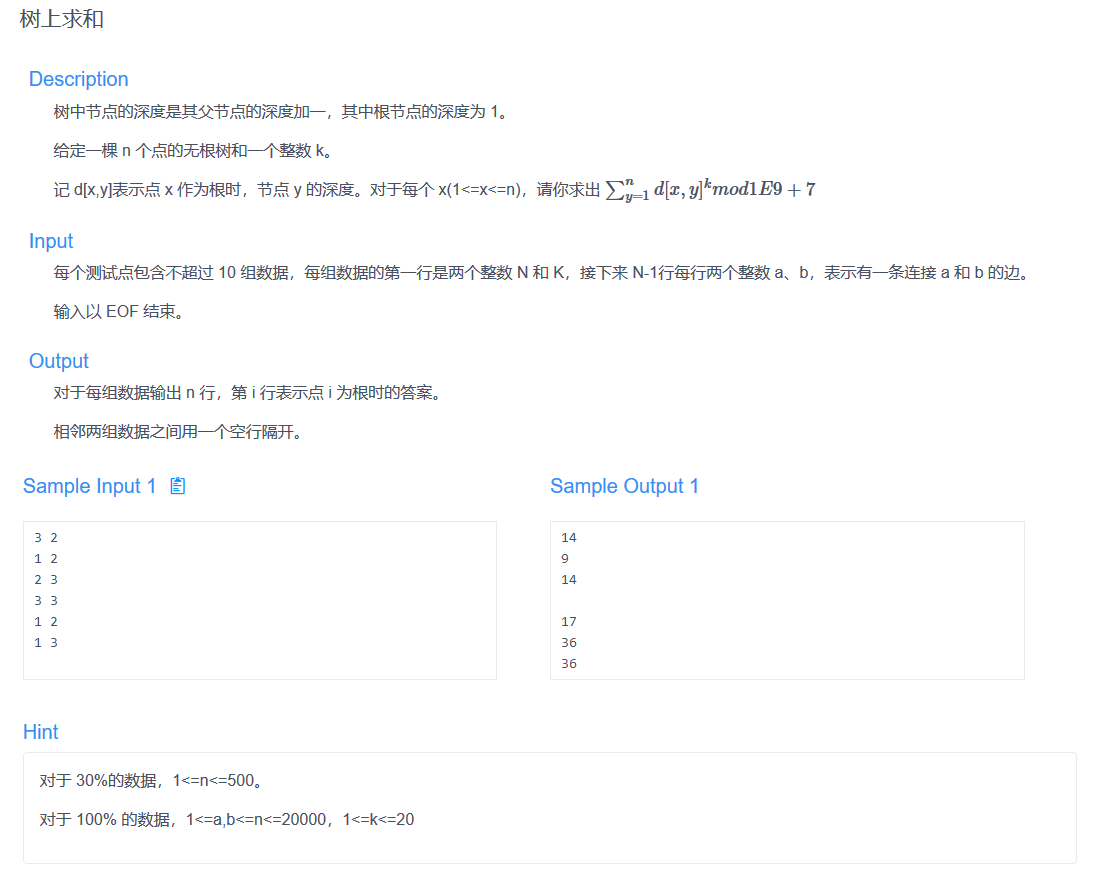
如果只是求和应该怎样做?一个很显然的换根树状DP。
现在要求k次呢?这样的话距离+1-1就需要进行变化了。
我们维护x^0~x^k的一个多项式，在更新x^k的时候利用二项式定理和更低次的项进行更新就好了。
这样一次更新复杂度O(k)，总复杂度O(nkt)，稳稳地AC了。
根节点深度为1好评，省去了对于0^k等问题的繁琐的分类讨论......
代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define debug cout
typedef long long int lli;
using namespace std;
const int maxn=2e4+1e2,maxk=25;
const int mod=1e9+7;


lli c[maxk][maxk];
int n,k;

namespace Pre {
    lli fac[maxk],inv[maxk];
    inline lli fastpow(lli base,int tim) {
        lli ret = 1;
        while( tim ) {
            if( tim & 1 ) ret = ret * base % mod;
            if( tim >>= 1 ) base = base * base % mod;
        }
        return ret;
    }
    inline lli C(int n,int m) {
        return fac[n] * inv[m] % mod * inv[n-m] % mod;
    }
    inline void work() {
        *fac = 1;
        for(int i=1;i<=k;i++) fac[i] = fac[i-1] * i % mod;
        inv[k] = fastpow(fac[k],mod-2);
        for(int i=k;i;i--) inv[i-1] = inv[i] * i % mod;
        for(int i=0;i<=k;i++)
            for(int j=0;j<=i;j++)
                c[i][j] = C(i,j);
    }
}

struct Poly {
    lli dat[maxk];
    Poly() {
        memset(dat,0,sizeof(dat));
    }
    lli& operator [] (const int &x) {
        return dat[x];
    }
    const lli& operator [] (const int &x) const {
        return dat[x];
    }
    friend Poly operator + (const Poly &a,const Poly &b) {
        Poly ret;
        for(int i=0;i<=k;i++)
            ret[i] = ( a[i] + b[i] ) % mod;
        return ret;
    }
    friend Poly operator - (const Poly &a,const Poly &b) {
        Poly ret;
        for(int i=0;i<=k;i++)
            ret[i] = ( a[i] - b[i] + mod ) % mod;
        return ret;
    }
    friend Poly operator + (const Poly &a,lli x) {
        Poly ret; x = ( x + mod ) % mod;
        static lli pows[maxk];
        *pows = 1;
        for(int i=1;i<=k;i++) pows[i] = pows[i-1] * x % mod;
        for(int i=k;~i;i--) {
            for(int j=i;~j;j--)
                ret[i] += a[j] * pows[i-j] % mod * c[i][j] % mod , ret[i] %= mod;
        }
        return ret;
    }
    inline void init() {
        for(int i=0;i<=k;i++) dat[i] = 1;
    }
}sson[maxn],sfa[maxn],f[maxn];
// sson is dis of points in subtree to pos .

int s[maxn],t[maxn<<1],nxt[maxn<<1],fa[maxn],cnt;

inline void addedge(int from,int to) {
    t[++cnt] = to , nxt[cnt] = s[from] , s[from] = cnt;
}
inline void dfsson(int pos) {
    sson[pos].init();
    for(int at=s[pos];at;at=nxt[at]) if( t[at] != fa[pos] ) {
        fa[t[at]] = pos , dfsson(t[at]);
        sson[pos] = sson[pos] + ( sson[t[at]] + 1 ) ;
    }
}
inline void dfsfa(int pos) {
    if( fa[pos] ) {
        sfa[pos] = sfa[fa[pos]] + 1;
        Poly delta = sson[fa[pos]] - ( sson[pos] + 1 );
        sfa[pos] = sfa[pos] + ( delta + 1 );
    }
    for(int at=s[pos];at;at=nxt[at]) if( t[at] != fa[pos] ) dfsfa(t[at]);
}
inline void getans() {
    for(int i=1;i<=n;i++) {
        Poly sum = sfa[i] + sson[i];
        printf("%lld\n",sum.dat[k]);
    }
    putchar('\n');
}

int main() {
    while( scanf("%d%d",&n,&k) == 2 ) {
        memset(s,0,sizeof(int)*(n+1)) , cnt = 0;
        Pre::work();
        for(int i=1,a,b;i<n;i++) {
            scanf("%d%d",&a,&b) ,
            addedge(a,b) , addedge(b,a);
        }
        dfsson(1) , dfsfa(1);
        getans();
    }
    return 0;
}

 

最后上排名。
(为什么3个AK的?因为有一个是我用我老婆的名字注册的账号(四蒸心.jpg))

话说比赛还没结束呢就发题解真的好吗?
另外我的桌子竟然带电!准备报警了!