北京集训:20180320

爆零蒟蒻欢乐多......

T1:

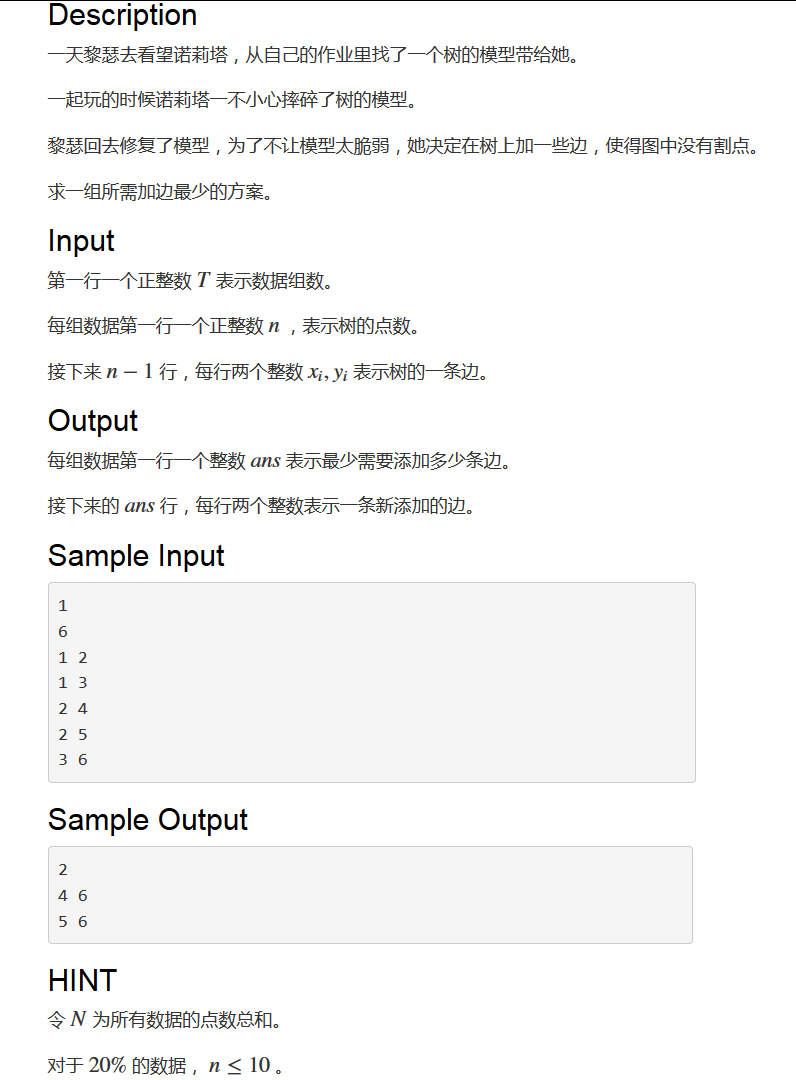
怎么又是构造题啊......
算了扔了不看了......
事实证明这种选择似乎是正确的......
我们直接来看正解:

考虑为什么我们把不同子树的叶子节点连接起来是正确的。
考虑我们割掉一个点，如果他是叶子节点，则原图显然还是联通的。
而如果他不是叶子节点，则他的子树可以通过那些叶子节点连的边通过根节点的其他子树与根节点互连。
所以这个东西显然是正确的，而题解取的max，是因为我们每个叶子节点都必须要连边，
而对于每一个点，分开他形成的叶子节点的子树们都需要互连。
考虑怎么构造，我们先找到重心，并dfs出以他为根的各个子树中的叶子节点。
然后我们钦定一个节点作为hub，其余节点两两配对，如果无法配对则与hub连接。
而为了避免同一个子树内的节点不得不相连(显然这样不优)，我们需要把这些子树按照大小排序，连边的时候按照一个从大到小启发式的顺序连接。
为什么，因为重心的每一个子树中的叶子节点个数一定不大于(fulleaf+1)/2。(否则我们可以调整重心位置是吧)
正解代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
#define debug cout
using namespace std;
const int maxn=5e5+1e2;

int s[maxn],t[maxn<<1],nxt[maxn<<1],deg[maxn],cnt;
int mx[maxn],sizleaf[maxn],full;
vector<int> leafs[maxn];
priority_queue<pair<unsigned,int> > pq;
vector<pair<int,int> > ans;
int n;

inline void addedge(int from,int to) {
    ++deg[to];
    t[++cnt] = to , nxt[cnt] = s[from] , s[from] = cnt;
}
inline void pre(int pos,int fa) {
    mx[pos] = sizleaf[pos] = ( deg[pos] == 1 );
    for(int at=s[pos];at;at=nxt[at]) if( t[at] != fa ) {
        pre(t[at],pos) , sizleaf[pos] += sizleaf[t[at]] , 
        mx[pos] = max(mx[pos],sizleaf[t[at]]);
    }
}
inline void dfs(int pos,int fa) {
    if( deg[pos] == 1 ) return leafs[full].push_back(pos);
    for(int at=s[pos];at;at=nxt[at]) if( t[at] != fa ) dfs(t[at],pos);
}

inline bool cmp(const vector<int> &a,const vector<int> &b) {
    return a.size() > b.size();
}
inline void repush(int p) {
    leafs[p].pop_back();
    if( leafs[p].size() ) pq.push(make_pair(leafs[p].size(),p));
}
inline void solve_case() {
    pre(1,-1);
    const int fulleaf = sizleaf[1];
    int cent = 1;
    for(int i=1;i<=n;i++) {
        mx[i] = max( mx[i] , fulleaf - sizleaf[i] );
        if( mx[i] < mx[cent] ) cent = i;
    }
    for(int at=s[cent];at;at=nxt[at]) {
        ++full;
        dfs(t[at],cent);
    }
    sort(leafs+1,leafs+1+full,cmp);
    pq.push(make_pair(leafs[1].size(),1));
    const int tp = leafs[1].back();
    for(int i=2;i<=full;i++)
        if( leafs[i].size() ) {
            if( pq.empty() ) {
                ans.push_back(make_pair(leafs[i].back(),tp));
            } else {
                const int j = pq.top().second; pq.pop();
                ans.push_back(make_pair(leafs[i].back(),leafs[j].back()));
                repush(j);
            }
            repush(i);
        }
    while( pq.size() ) {
        const int i = pq.top().second; pq.pop();
        if( !pq.size() ) {
            ans.push_back(make_pair(leafs[i].back(),tp));
        } else {
            const int j = pq.top().second; pq.pop();
            ans.push_back(make_pair(leafs[i].back(),leafs[j].back()));
            repush(j);
        }
        repush(i);
    }
    printf("%u\n",(unsigned)ans.size());
    for(unsigned i=0;i<ans.size();i++) printf("%d %d\n",ans[i].first,ans[i].second);
}

inline void reset() {
    #define mem(x) memset(x,0,sizeof(*x)*(n+1))
    mem(s) , mem(deg) , mem(mx) , mem(sizleaf);
    cnt = full = 0 , ans.clear();
    for(int i=0;i<=n;i++) leafs[i].clear();
    while( pq.size() ) pq.pop();
}

int main() {
    static int T;
    scanf("%d",&T);
    while(T--) {
        scanf("%d",&n) , reset();
        for(int i=1,a,b;i<n;i++) {
            scanf("%d%d",&a,&b) ,
            addedge(a,b) , addedge(b,a);
        }
        solve_case();
    }
    return 0;
}

T2:

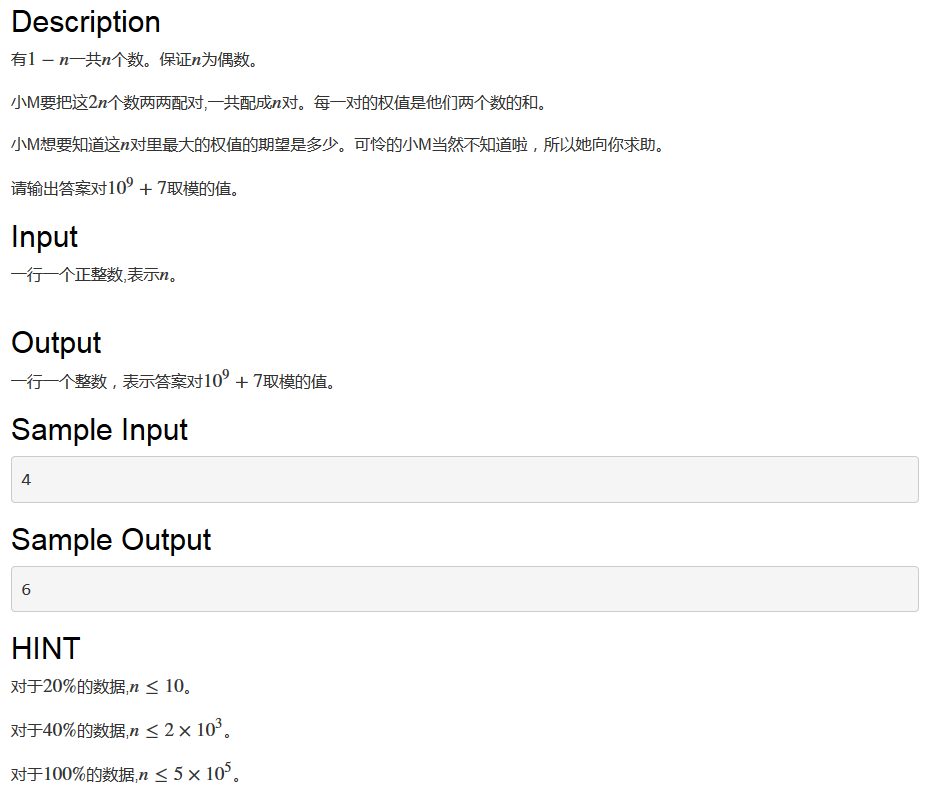
看起来很可做的样子啊。
这种期望一看就是先算出总和再除总方案数......
考虑我们怎么计算，20分可以爆搜......
然后看到40分的部分分，考虑n^2怎么做。
我们枚举最大一组的值，然后求让最大的一组的值正好为我们枚举的值的方案数。
然后发现我不会做，但是我们可以求出最大一组<=某个值的方案数，然后差分一下就能得到我们想要的东西。
方法就是我们从后向前遍历这些数字，考虑大于n/2的数字是怎么匹配的。
那么他能匹配的数字的限制就是当前值v-他本身的大小i，当然还要减去比他大的数字用掉的数字数量used(显然他们的方案一定是这个数的方案的子集)。
这样发现你会WA，因为我们可能会计算到自己对自己或者自己对比自己大的数的匹配......
好的，我们让前面的限制与 n-大于等于自己的数字的个数 取min就好了......
于是你get到了40分(我在考场上也就能想到这些了QAQ)。
其实正解已经很接近了......
仔细分析刚才的过程，是不是有一些数他的匹配方案的数量相同?还有一些数可以随意配对?
我们考虑按照限定的最大值v分组，显然>v/2的数字一定要与<v/2的数字配对。
这样的话，这些数的配对方案数就是(n-v/2)^(v/2)，注意这里的/2是下取整。
为什么这是对的？考虑后面的数每递减1，前面可选的区间递增1，而更大的数又用掉了一个，所以可用的数的数量不变。
考虑剩下的数怎么配对，假设剩下的数为x个，显然x一定是一个偶数(你告诉我 n-(v/2)*2 怎么能是奇数?），且他们可以两两配对。
那么方案数为x!/((x/2)!*2^x)。
为什么？我们先枚举全排列，钦定相邻的两个数配对，那么我们每个组内无序，所有组间无序，我们除去他们的排列即可。
考场40分代码:

#include<cstdio>
#include<algorithm>
typedef long long int lli;
const int maxn=5e3+1e2;
const int mod=1e9+7;

lli ways[maxn<<1],sum,full;
int n;

inline lli getinv(lli base) {
    lli ret = 1;
    int tim = mod - 2;
    while( tim ) {
        if( tim & 1 ) ret = ret * base % mod;
        if( tim >>= 1 ) base = base * base % mod;
    }
    return ret;
}

inline lli calc(int x) {
    lli ret = 1;
    int used = 0;
    for(int i=n;i>(n>>1);i--) {
        ret = ret * ( std::min(n-used-1,x-i) - used ) % mod;
        ++used;
    }
    return ret;
}

int main() {
    scanf("%d",&n);
    for(int i=n+1;i<n+n;i++) ways[i] = calc(i);
    for(int i=n+1;i<n+n;i++) {
        ( sum += ( ways[i] - ways[i-1] + mod ) % mod * i % mod ) %= mod ,
        ( full += ( ways[i] - ways[i-1] + mod ) % mod ) %= mod;
    }
    printf("%lld\n",sum*getinv(full)%mod);
    return 0;
}

正解代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define debug cout
typedef long long int lli;
using namespace std;
const int maxn=5e5+1e2,lim=5e5;
const int mod=1e9+7;

lli sum,full;
lli fac[maxn],inv[maxn],in[maxn<<1];
inline lli fastpow(lli base,int tim) {
    lli ret = 1;
    while( tim ) {
        if( tim & 1 ) ret = ret * base % mod;
        if( tim >>= 1 ) base = base * base % mod;
    }
    return ret;
}

inline void pre() {
    *fac = 1;
    for(int i=1;i<=lim;i++) fac[i] = fac[i-1] * i  % mod;
    inv[lim] = fastpow(fac[lim],mod-2);
    for(int i=lim;i;i--) inv[i-1] = inv[i] * i % mod;
}
inline lli f(lli x) {
    return fac[x] * inv[x>>1] % mod * fastpow(inv[2],x>>1) % mod;
}
inline lli g(int n,int v) {
    int l = n - ( v >> 1 );
    return fastpow(v-n,l) * f(n-(l<<1)) % mod;
}

int main() {
    static int n;
    scanf("%d",&n) , pre();
    for(int i=n+1;i<n<<1;i++) in[i] = g(n,i);
    for(int i=n+1;i<n<<1;i++) {
        const lli siz = ( in[i] - in[i-1] + mod ) % mod;
        ( sum += siz * i % mod ) %= mod ,
        ( full += siz ) %= mod;
    }
    printf("%lld\n",sum*fastpow(full,mod-2)%mod);
    return 0;
}

T3:

显然有一个O(n^2)的暴力区间DP......
然后前缀和in[i]+=in[i-1]写成了in[i]+=in[i+1]，爆零了......
正解是一个复杂度玄学的东西:

考虑我们每次的拓展过程，遍历整个可行的区间，如果可以拓展则拓展，显然这种贪心拓展是不会让答案变得更劣的。
然后发现我们无法贪心拓展了，这样我们就必须钦定一边的边界移动。
首先判定一定无解的情况，然后当前的情况就可能有解。
然后我们进行移动，而如果移动后变得非法，则直接返回无解。
为什么么这是正确的?显然l--和r++的两个条件不可能同时满足，否则可以贪心拓展。
(上面那句话为我口胡，其实正确性我也不是很明白......)
考场爆零代码(修改前缀和后有30分):

#include<cstdio>
#include<cstring>
typedef long long int lli;
const int maxn=1e3+1e2;

lli in[maxn];
bool f[maxn][maxn];

int main() {
    static int T,n,k;
    scanf("%d",&T);
    while(T--) {
        scanf("%d%d",&n,&k) , memset(f,0,sizeof(f)) , f[k][k] = 1;
        for(int i=1;i<=n;i++) scanf("%lld",in+i) , in[i] += in[i+1];
        for(int len=2;len<=n;len++)
            for(int st=1,ed;(ed=st+len-1)<=n;st++)
                if( in[ed] - in[st] <= 0 )
                    f[st][ed] |= f[st+1][ed] , f[st][ed] |= f[st][ed-1];
        puts(f[1][n]?"Yes":"No");
    }
    return 0;
}

正解代码:

#include<cstdio>
typedef long long int lli;
const int maxn=1e5+1e2;

lli in[maxn];
lli prvmi[maxn],prvmx[maxn],sufmi[maxn],sufmx[maxn];
int n,k;

inline void pre(lli* dst,int st,int delta,lli (calc)(lli,lli)) {
    dst[st] = in[st];
    for(int i=st+delta;1<=i&&i<=n;i+=delta)
        dst[i] = calc(in[i],dst[i-delta]);
}
inline lli _min(lli a,lli b) {
    return a < b ? a : b;
}
inline lli _max(lli a,lli b) {
    return a < b ? b : a;
}

inline bool calc() {
    for(int i=1;i<=n;i++) in[i] += in[i-1];
    pre(prvmi,1,1,_min) , pre(prvmx,1,1,_max) ,
    pre(sufmi,n,-1,_min) , pre(sufmx,n,-1,_max);
    
    int l = k , r = k;
    while( l != 1 || r != n ) {
        bool failed = 0;
        while( !failed ) {
            failed = 1;
            for(int i=l-1;i&&in[i]>=in[r];i--)
                if( in[i] >= in[l] ) l = i , failed = 0;
            for(int i=r+1;i<=n&&in[i]<=in[l];i++)
                if( in[i] <= in[r] ) r = i , failed = 0;
        }
        if( prvmx[l] < sufmi[r] || in[l] < in[r] ) return 0; // Not fixed
        if( l == 1 && r == n ) return 1;
        if( l == 1 ) ++r; // Do some operation which may be illeagle .
        else if( r == n ) --l;
        else {
            if( prvmx[l-1] < sufmx[r+1] && prvmi[l-1] < sufmi[r+1] ) return 0; // No way to extend .
            if( prvmx[l-1] >= sufmx[r+1] ) --l;
            else ++r;
        }
        if( prvmx[l] < sufmi[r] || in[l] < in[r] ) return 0;
    }
    return 1; // It may be (1,n] after extended .
}

int main() {
    static int T;
    scanf("%d",&T);
    while(T--) {
        scanf("%d%d",&n,&k);
        for(int i=1;i<=n;i++) scanf("%lld",in+i);
        puts(calc()?"Yes":"No");
    }
    return 0;
}

解放什么的，真的存在吗?

https://music.163.com/#/song?id=473403621