北京集训:20180316

吃了某种抑制神经的药的蒟蒻真是药丸......
别问我为什么推到今天才补，才不告诉你我拖延症犯了......

T1:

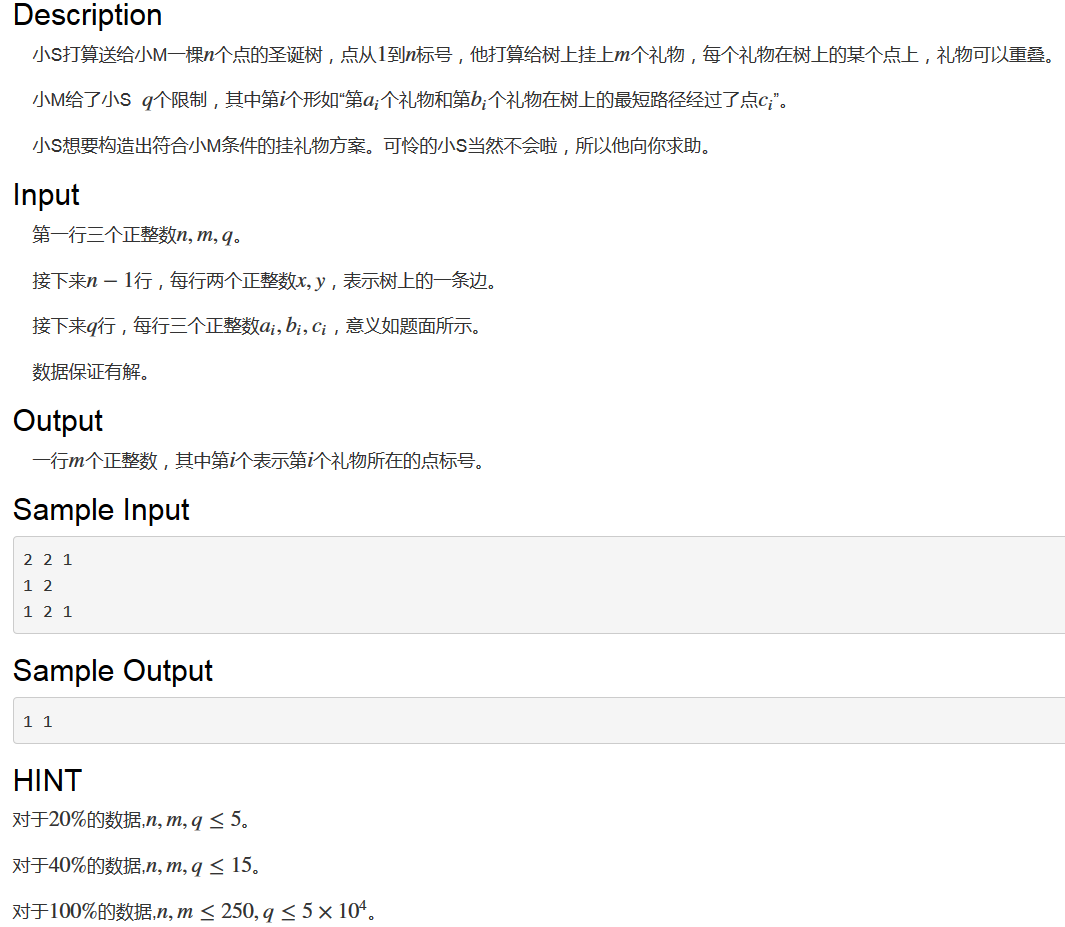
一看就是不可做的构造题......
前20分爆搜，后20分估计是什么状压，然而并不会写......
考虑f[i][j][k][l]表示礼物i在j，k在l是否可行，
我们可以通过一个类似于点分治的dfs预处理出这些信息。
如果我们把每个礼物在某个节点看做新图上一个点的话，我们就要在新图上找一个大小为n的团......
最大团什么的，不是NP问题吗?这玩意人干事?
算了，写个爆搜搞搞就好......
成绩出来发现跑过了4个点，第一个点WA了woc......
正解是2-sat。
考虑f[i][j][0/1]表示礼物i是否在点j的的子树中。
那么对于礼物x,y经过点pos，我们需要:
f[son][x]&f[son][y] = 0
f[pos][x]|f[pos][y] = 1
f[son][x]&f[son2][x] = 0
f[pos][x] -> f[fa][x]。
然后2-sat建图按照tarjan求出强连通的顺序输出方案即可。
然而写挂了还是30分......
考场30分暴力:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#include<bitset>
using namespace std;
const int maxn=252;

int s[maxn],t[maxn<<1],nxt[maxn<<1];
bitset<maxn> can[maxn][maxn][maxn],now[maxn][maxn];
bitset<maxn> sons[maxn],full;
vector<pair<int,int> > vs[maxn];
bool bad[maxn][maxn];
int fm[maxn],ans[maxn];
int n,m,q;

inline void addedge(int from,int to) {
    static int cnt = 0;
    t[++cnt] = to , nxt[cnt] = s[from] , s[from] = cnt;
}
inline void dfs(int pos,int fa,int bel) {
    sons[bel][pos] = 1 , fm[pos] = bel;
    for(int at=s[pos];at;at=nxt[at]) if( t[at] != fa ) dfs(t[at],pos,bel);
}
inline void solvepos(int pos) {
    if( !vs[pos].size() ) return;
    for(int at=s[pos];at;at=nxt[at]) {
        sons[t[at]] &= 0;
        dfs(t[at],pos,t[at]);
    }
    for(unsigned j=0;j<vs[pos].size();j++) {
        const int x = vs[pos][j].first , y = vs[pos][j].second;
        for(int i=1;i<=n;i++) if( i != pos ) {
            can[x][i][y] &= ( full ^ sons[fm[i]] );
            can[y][i][x] &= ( full ^ sons[fm[i]] );
        }
    }
}
inline void cpy(int dst,int sou) {
    for(int i=1;i<=m;i++) now[dst][i] = now[sou][i];
}
inline void afs(int pos) {
    if( pos == 1 ) {
        for(int i=1;i<=m;i++)
            for(int j=1;j<=m;j++)
                now[i][j] = full;
    }
    if( pos > m ) {
        for(int i=1;i<=m;i++) printf("%d%c",ans[i],i!=m?' ':'\n');
        exit(0);
    }
    for(int i=1,fail;i<=n;i++) if( now[pos][pos][i] && !bad[pos][i] ) {
        ans[pos] = i , fail = 0;
        cpy(pos+1,pos);
        for(int j=1;j<=m;j++) {
            now[pos+1][j] &= can[pos][i][j];
            if( !now[pos+1][j].count() ) {
                fail = 1;
                break;
            }
        }
        if( !fail ) afs(pos+1);
    }
}
inline void getbad() {
    for(int i=1;i<=m;i++)
        for(int j=1;j<=n;j++)
            for(int k=1;k<=m;k++)
                if( !can[i][j][k].count() ) {
                    bad[i][j] = 1;
                    break;
                }
}
int main() {
    scanf("%d%d%d",&n,&m,&q);
    for(int i=1,a,b;i<n;i++) {
        scanf("%d%d",&a,&b);
        addedge(a,b) , addedge(b,a);
    }
    for(int i=1,a,b,t;i<=q;i++) {
        scanf("%d%d%d",&a,&b,&t);
        vs[t].push_back(make_pair(a,b));
    }
    for(int i=1;i<=n;i++) full[i] = i;
    for(int i=1;i<=m;i++) for(int j=1;j<=n;j++) for(int k=1;k<=m;k++) can[i][j][k] = full;
    for(int i=1;i<=n;i++) solvepos(i);
    getbad();
    afs(1);
    return 0;
}

写挂的30分正解:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#define debug cout
using namespace std;
const int maxn=13000,maxe=6300000,maxl=300;

int n,m;
int ans[maxl],dep[maxl];

namespace Tsat {
    int s[maxn],t[maxe],nxt[maxe];
    int vis[maxn],dfn[maxn],low[maxn],bel[maxn],dd,iid;
    int ins[maxn],stk[maxn],top;
    inline void addedge(int from,int to) {
        static int cnt = 0;
        t[++cnt] = to , nxt[cnt] = s[from] , s[from] = cnt;
    }
    inline int cov(int pri,int pos,int sta) { // sta == 0 means not , sta == 1 means yes .
        return m * 2 * ( pri - 1 ) + ( pos - 1 ) * 2 + 1 + sta;
    }
    inline void dfs(int pos) {
        vis[pos] = 1;
        stk[++top] = pos , ins[pos] = 1;
        low[pos] = dfn[pos] = ++dd;
        for(int at=s[pos];at;at=nxt[at])
            if( !vis[t[at]] ) {
                dfs(t[at]);
                low[pos] = min( low[pos] , low[t[at]] );
            } else if( ins[t[at]] ) low[pos] = min( low[pos] , dfn[t[at]] );
        if( low[pos] == dfn[pos] ) {
            ++iid;
            do {
                const int x = stk[top--];
                bel[x] = iid , ins[x] = 0;
            } while( ins[pos] );
        }
    }
    inline void findway() {
        for(int i=1;i<=m;i++) ans[i] = 1;
        for(int i=1;i<=m;i++)
            for(int j=1;j<=n;j++) {
                const int c0 = cov(i,j,0) , c1 = cov(i,j,1);
                if( bel[c1] < bel[c0] && dep[ans[i]] < dep[j] ) ans[i] = j;
            }
    }
    inline void work() {
        for(int i=1;i<=n*m*2;i++) if( !vis[i] ) dfs(i);
        findway();
    }
}

namespace Tree {
    int s[maxl],t[maxl<<1],nxt[maxl<<1];
    vector<pair<int,int> > vec[maxl];
    inline void addedge(int from,int to) {
        static int cnt = 0;
        t[++cnt] = to , nxt[cnt] = s[from] , s[from] = cnt;
    }
    inline void dfs(int pos,int fa) {
        vector<int> sons;
        for(int at=s[pos];at;at=nxt[at]) if( t[at] != fa ) {
            sons.push_back(t[at]);
            dep[t[at]] = dep[pos] + 1 , dfs(t[at],pos);
        }
        #define cov(x,y,z) Tsat::cov(x,y,z)
        #define _addedge(a,b) Tsat::addedge(a,b)
        for(unsigned i=0;i<vec[pos].size();i++) {
            const int x = vec[pos][i].first , y = vec[pos][i].second;
            for(unsigned j=0;j<sons.size();j++) {
                const int c = sons[j];
                _addedge(cov(x,c,1),cov(y,c,0)) ,
                _addedge(cov(y,c,1),cov(x,c,0)) ;
            }
            _addedge(cov(x,pos,0),cov(y,pos,1)) ,
            _addedge(cov(y,pos,0),cov(x,pos,1)) ;
        }
        if( ~fa ) for(int k=1;k<=m;k++) _addedge(cov(k,pos,1),cov(k,fa,1));
        for(unsigned i=0;i<sons.size();i++)
            for(unsigned j=i+1;j<sons.size();j++)
                for(int k=1;k<=m;k++) {
                    const int x = sons[i] , y = sons[j];
                    _addedge(cov(k,x,1),cov(k,y,0)) ,
                    _addedge(cov(k,y,1),cov(k,x,0)) ;
                }
    }
}

int main() {
    static int q;
    scanf("%d%d%d",&n,&m,&q);
    for(int i=1,a,b;i<n;i++) {
        using Tree::addedge;
        scanf("%d%d",&a,&b) , addedge(a,b) , addedge(b,a);
    }
    for(int i=1,a,b,c;i<=q;i++) {
        using Tree::vec;
        scanf("%d%d%d",&a,&b,&c) , vec[c].push_back(make_pair(a,b));
    }
    dep[1] = 1;
    Tree::dfs(1,-1);
    Tsat::work();
    for(int i=1;i<=m;i++) printf("%d%c",ans[i],i!=m?' ':'\n');
    return 0;
}

/*
5 5 5
1 2
1 3
3 4
2 5
1 1 2
2 4 2
5 4 2
2 4 5
1 4 1

2 5 1 1 2
*/

Commit @ 2018.03.19
这个2sat终于调对了......
其实我们还需要加一条边:!f[fa][x] -> !f[pos][x]。
然后就是数组又开小了，250*250是1.3e5级别的，我开了1.3e4......
真·蒟蒻不识数
代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#define debug cout
using namespace std;
const int maxn=130000,maxe=6300000,maxl=300;

int n,m;
int ans[maxl],dep[maxl];

vector<pair<int,int> > es;
namespace Tsat {
    int s[maxn],t[maxe],nxt[maxe];
    int vis[maxn],dfn[maxn],low[maxn],bel[maxn],dd,iid;
    int ins[maxn],stk[maxn],top;
    inline void addedge(int from,int to) {
        static int cnt = 0;
        t[++cnt] = to , nxt[cnt] = s[from] , s[from] = cnt;
        es.push_back(make_pair(from,to));
    }
    inline int cov(int pri,int pos,int sta) { // sta == 0 means not , sta == 1 means yes .
        return m * 2 * ( pri - 1 ) + ( pos - 1 ) * 2 + 1 + sta;
    }
    inline void dfs(int pos) {
        vis[pos] = 1;
        stk[++top] = pos , ins[pos] = 1;
        low[pos] = dfn[pos] = ++dd;
        for(int at=s[pos];at;at=nxt[at])
            if( !vis[t[at]] ) {
                dfs(t[at]);
                low[pos] = min( low[pos] , low[t[at]] );
            } else if( ins[t[at]] ) low[pos] = min( low[pos] , dfn[t[at]] );
        if( low[pos] == dfn[pos] ) {
            ++iid;
            do {
                const int x = stk[top--];
                bel[x] = iid , ins[x] = 0;
            } while( ins[pos] );
        }
    }
    inline void findway() {
        for(int i=1;i<=m;i++) ans[i] = 1;
        for(int i=1;i<=m;i++)
            for(int j=1;j<=n;j++) {
                const int c0 = cov(i,j,0) , c1 = cov(i,j,1);
                if( bel[c1] < bel[c0] && dep[ans[i]] < dep[j] ) ans[i] = j;
            }
    }
    inline void work() {
        for(int i=1;i<=n*m*2;i++) if( !vis[i] ) dfs(i);
        findway();
    }
}

namespace Tree {
    int s[maxl],t[maxl<<1],nxt[maxl<<1];
    vector<pair<int,int> > vec[maxl];
    vector<int> sons[maxl];
    inline void addedge(int from,int to) {
        static int cnt = 0;
        t[++cnt] = to , nxt[cnt] = s[from] , s[from] = cnt;
    }
    inline void dfs(int pos,int fa) {
        for(int at=s[pos];at;at=nxt[at]) if( t[at] != fa ) {
            sons[pos].push_back(t[at]);
            dep[t[at]] = dep[pos] + 1 , dfs(t[at],pos);
        }
        #define cov(x,y,z) Tsat::cov(x,y,z)
        #define _addedge(a,b) Tsat::addedge(a,b)
        for(unsigned i=0;i<vec[pos].size();i++) {
            const int x = vec[pos][i].first , y = vec[pos][i].second;
            for(unsigned j=0;j<sons[pos].size();j++) {
                const int c = sons[pos][j];
                _addedge(cov(x,c,1),cov(y,c,0)) ,
                _addedge(cov(y,c,1),cov(x,c,0)) ;
            }
            _addedge(cov(x,pos,0),cov(y,pos,1)) , 
            _addedge(cov(y,pos,0),cov(x,pos,1)) ;
        }
        if( ~fa ) for(int k=1;k<=m;k++) {
            _addedge(cov(k,pos,1),cov(k,fa,1));
            _addedge(cov(k,fa,0),cov(k,pos,0)); // !
        }
        for(unsigned i=0;i<sons[pos].size();i++)
            for(unsigned j=i+1;j<sons[pos].size();j++)
                for(int k=1;k<=m;k++) {
                    const int x = sons[pos][i] , y = sons[pos][j];
                    _addedge(cov(k,x,1),cov(k,y,0)) ,
                    _addedge(cov(k,y,1),cov(k,x,0)) ;
                }
    }
}

int main() {
    static int q;
    scanf("%d%d%d",&n,&m,&q);
    for(int i=1,a,b;i<n;i++) {
        using Tree::addedge;
        scanf("%d%d",&a,&b) , addedge(a,b) , addedge(b,a);
    }
    for(int i=1,a,b,c;i<=q;i++) {
        using Tree::vec;
        scanf("%d%d%d",&a,&b,&c) , vec[c].push_back(make_pair(a,b));
    }
    dep[1] = 1;
    Tree::dfs(1,-1);
    Tsat::work();
    sort(es.begin(),es.end());
    for(int i=1;i<=m;i++) printf("%d%c",ans[i],i!=m?' ':'\n');
    return 0;
}

T2:

显然有一个非常好写的k^2插值。
然而我连拉格朗日插值都不会......
写了个多项式取模乱搞，卡成O(k^3)一分没有......
只有第一个点的10分。
其实拉格朗日插值不用求出多项式的，只要把你需要求值的x带进去即可。
正解为下面的一堆......

求出g然后用g插n即可。
拉格朗日插值的作用大概就是是用小范围的信息计算大范围的信息。
考场10分代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#define debug cout
typedef long long int lli;
using namespace std;
const int maxn=4e3+1e2;
const int mod=1e9+7;

lli inv[maxn];
int in[maxn];
int k;

inline lli fastpow(lli base,int tim) {
    lli ret = 1;
    while( tim ) {
        if( tim & 1 ) ret = ret * base % mod;
        if( tim >>= 1 ) base = base * base % mod;
    }
    return ret;
}

struct Poly {
    lli dat[maxn];
    Poly(int aa=0,int bb=0) {
        memset(dat,0,sizeof(dat));
        dat[1] = ( aa % mod + mod ) % mod , dat[0] = ( bb % mod + mod ) % mod;
    }
    lli& operator [] (const int &x) {
        return dat[x];
    }
    const lli& operator [] (const int &x) const {
        return dat[x];
    }
    friend Poly operator * (const Poly &a,const Poly &b) {
        Poly ret;
        for(int i=0;i<k+2;i++) for(int j=0;j<k+2;j++) ( ret[i+j] += a[i] * b[j] % mod ) %= mod;
        return ret;
    }
    friend Poly operator / (const Poly &a,const Poly &b) {
        Poly ret,tp=a;
        int hgh = k+2;
        while( !b[hgh] ) --hgh;
        for(int i=(k+2)<<1;i>=hgh;i--) if( tp[i] ) {
            const lli mul = tp[i] * fastpow(b[hgh],mod-2);
            ret[i-hgh] = mul;
            for(int t=0;t<=hgh;t++) ( ( tp[i-t] -= b[hgh-t] * mul % mod ) += mod ) %= mod;
        }
        return ret;
    }
    friend Poly operator + (const Poly &a,const Poly &b) {
        Poly ret;
        for(int i=0;i<k+2;i++)
            ret[i] = ( a[i] + b[i] ) % mod;
        return ret;
    }
    friend Poly operator * (const Poly &a,const lli &t) {
        Poly ret;
        for(int i=0;i<k+2;i++) ret[i] = a[i] * t % mod;
        return ret;
    }
    inline lli calc(lli base) {
        lli ret = 0 , now = 1;
        for(int i=0;i<k;i++) {
            ( ret += now * dat[i] % mod ) %= mod ,
            now = now * base % mod;
        }
        return ret;
    }
}pol;

inline Poly getval() {
    Poly ret,pi(0,1),now;
    for(int i=0;i<k;i++) pi = pi * Poly(1,-i);
    for(int i=0;i<k;i++) {
        lli mul = in[i];
        for(int j=0;j<k;j++) if( i != j ) {
            mul = mul * inv[abs(i-j)] % mod;
            if( i - j < 0 ) mul = mod - mul;
        }
        now = pi / Poly(1,-i);
        ret = ret + now * mul;
    }
    return ret;
}

inline void getinv() {
    static lli fac[maxn];
    *fac = 1;
    for(int i=1;i<=k;i++) fac[i] = fac[i-1] * i % mod;
    inv[k] = fastpow(fac[k],mod-2);
    for(int i=k;i;i--) inv[i-1] = inv[i] * i % mod;
    for(int i=1;i<=k;i++) inv[i] = inv[i] * fac[i-1] % mod;
}

int main() {
    static int n,q;
    static lli ans;
    scanf("%d%d%d",&n,&k,&q) , ++k;
    for(int i=0;i<k;i++) scanf("%d",in+i);
    if( n < k ) {
        for(int i=0;i<=n;i++) ans = ( ans + in[i] * fastpow(q,i) % mod ) % mod;
        return printf("%lld\n",ans),0;
    }
    getinv();
    pol = getval();
    for(int i=0;i<=n;i++) ans = ( ans + pol.calc(i) * fastpow(q,i) % mod ) % mod;
    printf("%lld\n",ans);
    return 0;
}

修正40分暴力:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#define debug cout
typedef long long int lli;
using namespace std;
const int maxn=5e5+1e2;
const int mod=1e9+7;

struct Node {
    lli a,b;
    friend Node operator + (const Node &a,const Node &b) {
        return (Node){(a.a+b.a)%mod,(a.b+b.b)%mod};
    }
    friend Node operator * (const Node &a,const lli &x) {
        return (Node){a.a*x%mod,a.b*x%mod};
    }
    friend Node operator + (const Node &a,const lli &x) {
        return (Node){a.a,(a.b+x)%mod};
    }
}ns[maxn];

lli in[maxn],g[maxn],fac[maxn],inv[maxn];
int k,p;

inline lli fastpow(lli base,int tim) {
    lli ret = 1;
    while(tim) {
        if( tim & 1 ) ret = ret * base % mod;
        if( tim >>= 1 ) base = base * base % mod;
    }
    return ret;
}

inline void pre() {
    *fac = 1;
    for(int i=1;i<=k;i++) fac[i] = fac[i-1] * i % mod;
    inv[k] = fastpow(fac[k],mod-2);
    for(int i=k;i;i--) inv[i-1] = inv[i] * i % mod;
}
inline lli c(int n,int m) {
    return fac[n] * inv[m] % mod * inv[n-m] % mod;
}

namespace Inter {
    lli fac[maxn],facrev[maxn],pprv[maxn],ssuf[maxn],*prv=pprv+1,*suf=ssuf+1;
    inline lli getmul(int p) {
        return p ? fac[p] * facrev[k-p-1] % mod : facrev[k-1];
    }
    inline lli getval(lli* in,lli x) {
        lli ret = 0;
        prv[-1] = 1;
        for(int i=0;i<k;i++) prv[i] = prv[i-1] * (x-i+mod) % mod;
        suf[k] = 1;
        for(int i=k-1;~i;i--) suf[i] = suf[i+1] * (x-i+mod) % mod;
        for(int i=0;i<k;i++) {
            lli now = prv[i-1] * suf[i+1] % mod;
            ret = ret + now * in[i] % mod * getmul(i) % mod , ret %= mod;
        }
        return ret;
    }
    inline void getinv() {
        static lli inv[maxn];
        *fac = 1;
        for(int i=1;i<=k;i++) fac[i] = fac[i-1] * i % mod;
        inv[k] = fastpow(fac[k],mod-2);
        for(int i=k;i;i--)inv[i-1] = inv[i] * i % mod;
        for(int i=1;i<=k;i++) inv[i] = inv[i] * fac[i-1] % mod;
        for(int i=1;i<=k;i++) fac[i] = fac[i-1] * inv[i] % mod;
        facrev[0] = 1;
        for(int i=1;i<=k;i++) facrev[i] = facrev[i-1] * ( mod - inv[i] ) % mod;
    }
}

inline void getg0() {
    static Node now;
    int mul = 1;
    for(int i=0;i<=k;i++) {
        now = now + ns[k-i] * ( mul == 1 ? c(k,i) : mod - c(k,i) );
        mul *= -1;
    }
    g[0] = ( mod - now.b ) % mod * fastpow(now.a,mod-2) % mod;
}
inline void calc() {
    const lli inv = fastpow(p,mod-2);
    ns[0] = (Node){1,0};
    for(int i=1;i<=k;i++) ns[i] = ( ns[i-1] + in[i-1] ) * inv;
    getg0();
    for(int i=1;i<=k;i++) g[i] = ( g[i-1] + in[i-1] ) % mod * inv % mod;
}

int main() {
    static lli ans,n;
    scanf("%lld%d%d",&n,&k,&p) , ++k;
    for(int i=0;i<k;i++) scanf("%lld",in+i);
    pre() , calc();
    Inter::getinv();
    ans = ( Inter::getval(g,n+1) * fastpow(p,(n+1)%(mod-1)) % mod - g[0] + mod ) % mod;
    printf("%lld\n",ans);
    return 0;
}

正解代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#define debug cout
typedef long long int lli;
using namespace std;
const int maxn=5e5+1e2;
const int mod=1e9+7;

struct Node {
    lli a,b;
    friend Node operator + (const Node &a,const Node &b) {
        return (Node){(a.a+b.a)%mod,(a.b+b.b)%mod};
    }
    friend Node operator * (const Node &a,const lli &x) {
        return (Node){a.a*x%mod,a.b*x%mod};
    }
    friend Node operator + (const Node &a,const lli &x) {
        return (Node){a.a,(a.b+x)%mod};
    }
}ns[maxn];

lli in[maxn],g[maxn],fac[maxn],inv[maxn];
int k,p;

inline lli fastpow(lli base,int tim) {
    lli ret = 1;
    while(tim) {
        if( tim & 1 ) ret = ret * base % mod;
        if( tim >>= 1 ) base = base * base % mod;
    }
    return ret;
}
inline lli fastpow_lli(lli base,lli tim) {
    lli ret = 1;
    while(tim) {
        if( tim & 1 ) ret = ret * base % mod;
        if( tim >>= 1 ) base = base * base % mod;
    }
    return ret;
}

inline void pre() {
    *fac = 1;
    for(int i=1;i<=k;i++) fac[i] = fac[i-1] * i % mod;
    inv[k] = fastpow(fac[k],mod-2);
    for(int i=k;i;i--) inv[i-1] = inv[i] * i % mod;
}
inline lli c(int n,int m) {
    return fac[n] * inv[m] % mod * inv[n-m] % mod;
}

namespace Inter {
    lli fac[maxn],facrev[maxn],pprv[maxn],ssuf[maxn],*prv=pprv+1,*suf=ssuf+1;
    inline lli getmul(int p) {
        return p ? fac[p] * facrev[k-p-1] % mod : facrev[k-1];
    }
    inline lli getval(lli* in,lli x) {
        x %= mod;
        lli ret = 0;
        prv[-1] = 1;
        for(int i=0;i<k;i++) prv[i] = prv[i-1] * (x-i+mod) % mod;
        suf[k] = 1;
        for(int i=k-1;~i;i--) suf[i] = suf[i+1] * (x-i+mod) % mod;
        for(int i=0;i<k;i++) {
            lli now = prv[i-1] * suf[i+1] % mod;
            ret = ret + now * in[i] % mod * getmul(i) % mod , ret %= mod;
        }
        return ret;
    }
    inline void getinv() {
        static lli inv[maxn];
        *fac = 1;
        for(int i=1;i<=k;i++) fac[i] = fac[i-1] * i % mod;
        inv[k] = fastpow(fac[k],mod-2);
        for(int i=k;i;i--) inv[i-1] = inv[i] * i % mod;
        for(int i=1;i<=k;i++) inv[i] = inv[i] * fac[i-1] % mod;
        for(int i=1;i<=k;i++) fac[i] = fac[i-1] * inv[i] % mod;
        facrev[0] = 1;
        for(int i=1;i<=k;i++) facrev[i] = facrev[i-1] * ( mod - inv[i] ) % mod;
    }
}

inline void getg0() {
    static Node now;
    int mul = 1;
    for(int i=0;i<=k;i++) {
        now = now + ns[k-i] * ( mul == 1 ? c(k,i) : mod - c(k,i) );
        mul *= -1;
    }
    g[0] = ( mod - now.b ) % mod * fastpow(now.a,mod-2) % mod;
}
inline void calc() {
    const lli inv = fastpow(p,mod-2);
    ns[0] = (Node){1,0};
    for(int i=1;i<=k;i++) ns[i] = ( ns[i-1] + in[i-1] ) * inv;
    getg0();
    for(int i=1;i<=k;i++) g[i] = ( g[i-1] + in[i-1] ) % mod * inv % mod;
}

int main() {
    static lli ans,n;
    scanf("%lld%d%d",&n,&k,&p) , ++k;
    for(int i=0;i<k;i++) scanf("%lld",in+i);
    pre() , calc();
    Inter::getinv();
    ans = ( Inter::getval(g,n+1) * fastpow_lli(p,n+1) % mod - g[0] + mod ) % mod;
    printf("%lld\n",ans);
    return 0;
}

T3:

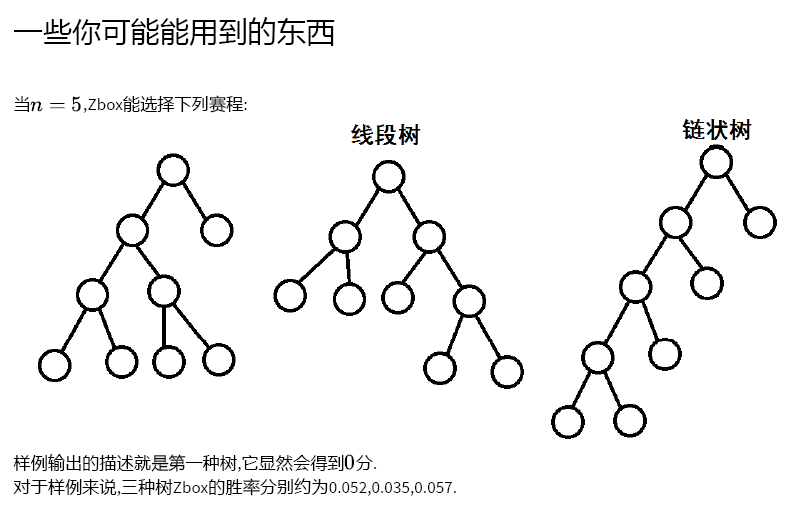
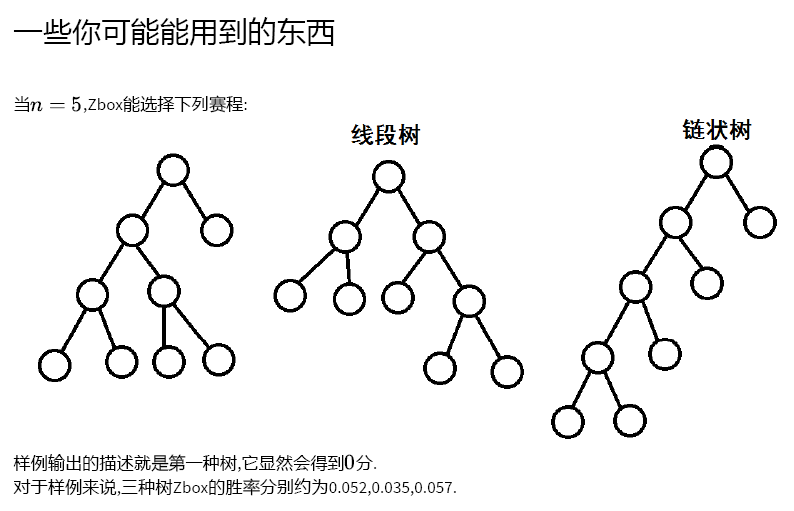
一个很不靠谱的构造题......
还有很不靠谱的题解......

不想改了，把标程丢上来吧......

#include<bits/stdc++.h>
#define lowbit(x) (x&(-x))
#define N 16
using namespace std;
int size[2*N],l[2*N],r[2*N],a[N],n;
double f[2*N][1<<N][N],fac[N];
vector<int> vec[N];
int ls[1<<N],ln,lg[1<<N];
int bitcount(int s){int ans=0;while (s) {ans++;s-=lowbit(s);}return ans;}
void dfs(int s)
{
    if (!l[s]) {size[s]=1;return;}
    dfs(l[s]);dfs(r[s]);
    size[s]=size[l[s]]+size[r[s]];
}
int st[18],top;
void gao(int now,int rem,int w)
{
    if (now>top) {ls[++ln]=w;return;}
    if (top-now>=rem) gao(now+1,rem,w);
    if (rem) gao(now+1,rem-1,w+st[now]);
}
void search(int s,int sz)
{
    top=0; 
    while (s)
    {
        st[++top]=lowbit(s);
        s-=lowbit(s);
    }
    gao(1,sz,0);
}
void work(int s)
{
    if (!l[s])
    {
        for (int i=0;i<n;i++) f[s][1<<i][i]=1;
        return;
    }
    work(l[s]);work(r[s]);
    double pp=fac[size[l[s]]]*fac[size[r[s]]]/fac[size[s]];
    for (int k=0;k<vec[size[s]].size();k++)
    {
        int d=vec[size[s]][k];
        ln=0;search(d,size[l[s]]);
        for (int kk=1;kk<=ln;kk++)
        {
            int dd=ls[kk];
            for (int ii=dd,i=lg[lowbit(ii)];ii;ii-=lowbit(ii),i=lg[lowbit(ii)])
            for (int jj=d-dd,j=lg[lowbit(jj)];jj;jj-=lowbit(jj),j=lg[lowbit(jj)])
            {
                double p=pp*f[l[s]][dd][i]*f[r[s]][d-dd][j]/(a[i]+a[j]);
                f[s][d][i]+=p*a[i];
                f[s][d][j]+=p*a[j];
            }
        }
    }
}
double zuo()
{
    memset(f,0,sizeof(f));
    memset(size,0,sizeof(size));
    dfs(1);work(1);
    return f[1][(1<<n)-1][0];
}
int tp;
int gen1(int n)
{
    int s=++tp;
    if (n==1) {l[s]=r[s]=0;return s;}
    int dv=1;
    l[s]=gen1(dv);r[s]=gen1(n-dv);
    return s;
}
int gen2(int n)
{
    int s=++tp;
    if (n==1) {l[s]=r[s]=0;return s;}
    int dv=n/2;
    l[s]=gen2(dv);r[s]=gen2(n-dv);
    return s;
}
int gen3(int n)
{
    int s=++tp;
    if (n==1) {l[s]=r[s]=0;return s;}
    int dv=rand()%(n-1)+1;
    l[s]=gen3(dv);r[s]=gen3(n-dv);
    return s;
}
int main()
{
    scanf("%d",&n);
    for (int i=0;i<=n;i++) lg[1<<i]=i;
    fac[0]=1;for (int i=1;i<=n;i++) fac[i]=fac[i-1]*i;
    for (int s=0;s<(1<<n);s++)
    {
        vec[bitcount(s)].push_back(s);
    }
    for (int i=0;i<n;i++) scanf("%d",&a[i]);
     
    int ll=1,rr=100;
    while (ll+1!=rr)
    {
        int mid=(ll+rr)>>1;a[0]=mid;
        double p1,p2;
        tp=0;gen1(n);p1=zuo();
        tp=0;gen2(n);p2=zuo();
        if (p1<p2) rr=mid;else ll=mid;
    }
    a[0]=ll;
    double p1,p2,ans;
    tp=0;gen1(n);p1=zuo();
    tp=0;gen2(n);p2=zuo();
    ans=max(p1,p2);
    while (1)
    {
        tp=0;gen3(n);
        if (zuo()>ans+1e-9)
        {
            printf("1\n1 %d\n",a[0]);
            for (int i=1;i<=2*n+1;i++) printf("%d %d\n",l[i],r[i]);
            return 0;
        }
    }
}