北京集训:20180310
北京集训的第一天,我完美爆零......
这其中的经历,十分有趣呢。
T1:


这题一看就是先猜一个性质然后利用他去求解。
如果我们知道怎么插入,怎么判定的话,可以线段树分治的说。
然后我猜了一个结论:如果稳定,则一定有一个x的四联通块能同时通向上下左右边界。
乍一看是对的,实际上这个东西充分,但不必要。
考虑3*3的网格图,我们染色左下角三个点,再染色右上角三个点,结果应该是稳定的。
然后这个算法就错了。
问题是由于我太菜了,故考场上并没有想到这个反例......
正解的确是线段树分治,然而他是用角度推的。
考虑对于一个四边形的四个定点,每个点在左上角的那个角,显然对角线的角和相同。
而如果一个格子为x,则他右下角和左上角的角度均为90度,相当于让另外两个角必须满足某些条件。
而如果这个条件让整个图都被限制的话,显然就固定了。
现在我们可以做什么?O(nmq)暴力。
然而正解要更加优美:
显然我们可以用第一行的所有角度和第一列的所有角度算出所有角,所以限制就相当于是行列连边。
经典的二分图模型啦。
然后用可回退并查集维护是否左右行列都在一个联通块里就好了QwQ。
考场爆零代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<vector> 6 #define debug cout 7 using namespace std; 8 const int maxn=9e6+1e2,maxl=3e3+1e2,maxq=1e5+1e2; 9 const int dx[]={1,-1,0,0},dy[]={0,0,1,-1}; 10 11 char in[maxl][maxl],now[maxl][maxl]; 12 int tim[maxl][maxl],ans[maxq]; 13 int l[maxq<<3],r[maxq<<3],lson[maxq<<3],rson[maxq<<3],cnt; 14 int fa[maxn],siz[maxn],sta[maxn]; 15 int n,m,q; 16 int pp; 17 18 struct ONode { 19 int x,y; 20 }; 21 vector<ONode> ns[maxq<<3]; 22 23 struct MemNode { 24 int *dst,val; 25 MemNode() {} 26 MemNode(int &x) { dst = &x , val = x; } 27 inline void res() { 28 *dst = val; 29 } 30 }stk[maxn]; 31 int top; 32 33 inline int findfa(int x) { 34 return fa[x] == x ? x : findfa(fa[x]); 35 } 36 inline bool merge(int x,int y) { 37 x = findfa(x) , y = findfa(y); 38 if( x == y ) return 0; 39 if( siz[x] < siz[y] ) swap(x,y); 40 if( pp != 1 ) stk[++top] = MemNode(siz[x]) , stk[++top] = MemNode(fa[y]) , stk[++top] = MemNode(sta[x]); 41 fa[y] = x , siz[x] += siz[y] , sta[x] |= sta[y]; 42 return sta[x] == 15; 43 } 44 45 inline void reset(int ltop) { 46 while( top > ltop ) stk[top].res() , --top; 47 } 48 inline int cov(int x,int y) { 49 return m * --x + y; 50 } 51 inline int operat(int x,int y) { 52 int ret = 0; 53 now[x][y] = 'x'; 54 ret |= ( sta[findfa(cov(x,y))] == 15 ); 55 for(int i=0;i<4;i++) { 56 const int tx = x + dx[i] , ty = y + dy[i]; 57 if( 0 < tx && tx <= n && 0 < ty && ty <= m && now[tx][ty] == 'x' ) ret |= merge(cov(x,y),cov(tx,ty)); 58 } 59 return ret; 60 } 61 62 inline void build(int pos,int ll,int rr) { 63 l[pos] = ll , r[pos] = rr; 64 if( ll == rr ) return; 65 const int mid = ( ll + rr ) >> 1; 66 build(lson[pos]=++cnt,ll,mid) , build(rson[pos]=++cnt,mid+1,rr); 67 } 68 inline void insert(int pos,int ll,int rr,const ONode &o) { 69 if( ll <= l[pos] && r[pos] <= rr ) { 70 ns[pos].push_back(o); 71 return; 72 } const int mid = ( l[pos] + r[pos] ) >> 1; 73 if( rr <= mid ) insert(lson[pos],ll,rr,o); 74 else if( ll > mid ) insert(rson[pos],ll,rr,o); 75 else insert(lson[pos],ll,rr,o) , insert(rson[pos],ll,rr,o); 76 } 77 inline void dfs(int pos,int stable) { 78 pp = pos; 79 const int memtop = top; 80 for(unsigned i=0;i<ns[pos].size();i++) stable |= operat(ns[pos][i].x,ns[pos][i].y); 81 if( l[pos] == r[pos] ) { 82 ans[l[pos]] = stable; 83 } 84 else dfs(lson[pos],stable) , dfs(rson[pos],stable); 85 if( pos != 1 ) { 86 reset(memtop); 87 for(unsigned i=0;i<ns[pos].size();i++) now[ns[pos][i].x][ns[pos][i].y] = 0; 88 } 89 } 90 91 int main() { 92 static int q; 93 scanf("%d%d%d",&n,&m,&q); 94 for(int i=1;i<=n;i++) { 95 scanf("%s",in[i]+1); 96 for(int j=1;j<=m;j++) if( in[i][j] == 'x' ) tim[i][j] = 1; 97 } 98 build(cnt=1,1,q+1); 99 for(int i=1,x,y;i<=q;i++) { 100 scanf("%d%d",&x,&y); 101 if( tim[x][y] ) { 102 insert(1,tim[x][y],i,(ONode){x,y}) , tim[x][y] = 0; 103 } 104 else tim[x][y] = i+1; 105 } 106 for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if( tim[i][j] ) { 107 insert(1,tim[i][j],q+1,(ONode){i,j}); 108 } 109 for(int i=1;i<=n;i++) 110 for(int j=1;j<=m;j++) { 111 const int c = cov(i,j); 112 fa[c] = c , siz[c] = 1; 113 if( i == 1 ) sta[c] |= 1; 114 if( j == 1 ) sta[c] |= 2; 115 if( i == n ) sta[c] |= 4; 116 if( j == m ) sta[c] |= 8; 117 } 118 dfs(1,0); 119 for(int i=1;i<=q+1;i++) puts(ans[i]?"S":"U"); 120 return 0; 121 }
考后AC代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<vector> 6 #include<stack> 7 #define debug cout 8 using namespace std; 9 const int maxn=9e6+1e2,maxl=3e3+1e2,maxq=3e5+1e2; 10 11 char in[maxl][maxl]; 12 int tim[maxl][maxl]; 13 int l[maxq<<2],r[maxq<<2],lson[maxq<<2],rson[maxq<<2],cnt; 14 int fa[maxn],siz[maxn]; 15 int ans[maxq]; 16 int n,m; 17 18 struct Node { 19 int x,y; 20 }; 21 vector<Node> ns[maxq<<2]; 22 struct StkNode { 23 int *dst,val; 24 StkNode() {} 25 StkNode(int &x) { dst = &x , val = x; } 26 inline void res() { *dst = val ; } 27 }stk[maxq<<2]; 28 int top; 29 30 inline int findfa(int x) { 31 return fa[x] == x ? x : findfa(fa[x]); 32 } 33 inline void merge(int x,int y,int pos) { 34 x = findfa(x) , y = findfa(y); 35 if( x == y ) return; 36 if( siz[x] < siz[y] ) swap(x,y); 37 if( pos != 1 ) stk[++top] = StkNode(fa[y]) , stk[++top] = StkNode(siz[x]); 38 fa[y] = x , siz[x] += siz[y]; 39 } 40 inline void reset(int last) { 41 while( top > last ) stk[top--].res(); 42 } 43 44 inline void build(int pos,int ll,int rr) { 45 l[pos] = ll , r[pos] = rr; 46 if( ll == rr ) return; 47 const int mid = ( ll + rr ) >> 1; 48 build(lson[pos]=++cnt,ll,mid) , 49 build(rson[pos]=++cnt,mid+1,rr) ; 50 } 51 inline void insert(int pos,int ll,int rr,const Node &o) { 52 if( ll <= l[pos] && r[pos] <= rr ) return ns[pos].push_back(o); 53 const int mid = r[lson[pos]]; 54 if( rr <= mid ) return insert(lson[pos],ll,rr,o); 55 if( ll > mid ) return insert(rson[pos],ll,rr,o); 56 insert(lson[pos],ll,rr,o) , 57 insert(rson[pos],ll,rr,o) ; 58 } 59 inline void dfs(int pos) { 60 const int mtop = top; 61 for(unsigned i=0;i<ns[pos].size();i++) merge(ns[pos][i].x,ns[pos][i].y+n,pos); 62 if( l[pos] == r[pos] ) ans[l[pos]] = ( siz[findfa(1)] == n + m ); 63 else dfs(lson[pos]) , dfs(rson[pos]); 64 if( pos != 1 ) reset(mtop); 65 } 66 67 int main() { 68 static int q; 69 scanf("%d%d%d",&n,&m,&q) , memset(tim,-1,sizeof(tim)); 70 for(int i=1;i<=n;i++) { 71 scanf("%s",in[i]+1); 72 for(int j=1;j<=m;j++) if( in[i][j] == 'x' ) tim[i][j] = 0; 73 } 74 build(cnt=1,0,q); 75 for(int i=1,x,y;i<=q;i++) { 76 scanf("%d%d",&x,&y); 77 if( ~tim[x][y] ) insert(1,tim[x][y],i-1,(Node){x,y}) , tim[x][y] = -1; 78 else tim[x][y] = i; 79 } 80 for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if( ~tim[i][j] ) insert(1,tim[i][j],q,(Node){i,j}); 81 for(int i=1;i<=n+m;i++) fa[i] = i , siz[i] = 1; 82 dfs(1); 83 for(int i=0;i<=q;i++) puts(ans[i]?"S":"U"); 84 return 0; 85 }
T2:

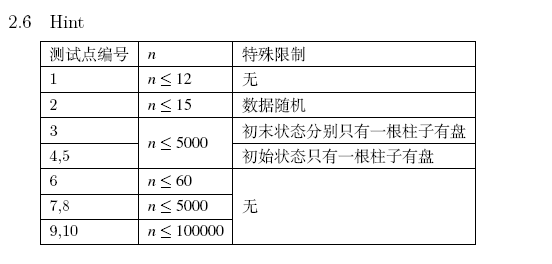
前两个测试点可以大力状压哈希bfs(不,大力bfs是过不去第二个测试点的)。
然后我们考虑分析一发:
首先我们只有三根柱子(废话)。
考虑最大的位置不对的盘子,我们一定要把他从一根柱子移动到另一根。
也就是说,我们需要让他所在的柱子为只有他,他需要到的柱子为空。
其他的盘子呢?必须都移到剩下的一个柱子上啊。这个步数大力计算一下就好了。
然后我们移动了最大的盘子,现在我们有一摞盘子和他们需要的地方。
一个一个摆放到位就可以了,反正(大概)只有一种不走重复步的方案吧。
接着你会发现你会WA,你过不了样例。
因为样例的最优解是把最大的盘子先放到中间。
好,这也是一种策略,我们把第一步的这种方式也考虑进去,反正接下来对一摞盘子的分析一定是对的。
关于我为什么爆零?考场上以为1是最大的盘子,然后直接贪心过了样例,自然也没有想第二种情况啦......
其实更正了看错题的问题还是有60分的。
考场爆零代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<bitset> 6 #include<map> 7 #include<queue> 8 #define lli long long int 9 #define ulli unsigned long long 10 #define debug cout 11 using namespace std; 12 const int maxn=1e6+1e2,mod=998244353; 13 const int base=17; 14 const int maxl=20; 15 16 int n; 17 18 namespace Sol { 19 int st[3][maxn],ed[3][maxn],now[3][maxn],n; 20 lli pows[maxn]; 21 22 inline int findmx(int sou[3][maxn]) { 23 int ret = -1; 24 for(int i=0;i<3;i++) 25 if( sou[i][0] && ( ret == -1 || sou[i][sou[i][0]] < sou[ret][sou[ret][0]] ) ) ret = i; 26 return ret; 27 } 28 inline int solve_merge(int siz,int tar) { 29 int xp = findmx(st); 30 while( siz && xp == tar ) st[xp][st[xp][0]] = 0 , st[xp][0]-- , siz-- , xp = findmx(st); 31 if( !siz ) return 0; 32 st[xp][st[xp][0]] = 0 , st[xp][0]--; 33 const int nt = 3 - xp - tar; 34 return ( solve_merge(siz-1,nt) + 1 + pows[siz-1] ) % mod; 35 } 36 37 inline void solve() { 38 int ms,me,siz=n; 39 lli ans = 0; 40 while( siz ) { 41 ms = findmx(st) , me = findmx(ed); 42 if( ms == me ) { 43 st[ms][st[ms][0]] = 0 , --st[ms][0]; 44 ed[me][ed[me][0]] = 0 , --ed[me][0]; 45 --siz; 46 } else break; 47 } 48 if( !siz ) { 49 puts("0"); 50 return; 51 } 52 int ftar = 3 - ms - me; 53 st[ms][st[ms][0]] = 0 , --st[ms][0]; 54 ed[me][ed[me][0]] = 0 , --ed[me][0]; 55 --siz; 56 ans = solve_merge(siz,ftar) + 1; 57 //debug<<"inital ans = "<<ans<<endl; 58 while( siz ) { 59 while( siz && ( me = findmx(ed) ) == ftar ) { 60 ed[me][ed[me][0]] = 0 , --ed[me][0]; 61 --siz; 62 } 63 if( !siz ) break; 64 ans = ( ans + pows[siz-1] + 1 ) % mod; 65 ftar = 3 - me - ftar; 66 ed[me][ed[me][0]] = 0 , --ed[me][0] , --siz; 67 } 68 ans = ( ans + mod ) % mod; 69 printf("%lld\n",ans); 70 } 71 int main() { 72 for(int i=1;i<=n;i++) pows[i] = ( ( pows[i-1] << 1 ) | 1 ) % mod; 73 for(int i=0;i<3;i++) { 74 scanf("%d",st[i]); 75 for(int j=1;j<=st[i][0];j++) scanf("%d",st[i]+j); 76 reverse(st[i]+1,st[i]+1+st[i][0]); 77 } 78 for(int i=0;i<3;i++) { 79 scanf("%d",ed[i]); 80 for(int j=1;j<=ed[i][0];j++) scanf("%d",ed[i]+j); 81 reverse(ed[i]+1,ed[i]+1+ed[i][0]); 82 } 83 solve(); 84 return 0; 85 } 86 } 87 88 namespace Force { 89 struct Statement { 90 bitset<maxl> s[3]; 91 inline ulli h() const { 92 ulli ret = 0; 93 for(int i=0;i<3;i++) 94 for(int j=1;j<=n;j++) 95 ret = ret * base + ( j * s[i][j] ); 96 return ret; 97 } 98 inline void findtop(int* ret) const { 99 for(int i=0;i<3;i++) { 100 ret[i] = 0; 101 for(int j=n;j;j--) 102 if( s[i][j] ) { 103 ret[i] = j; 104 break; 105 } 106 } 107 } 108 }st,ed; 109 110 map<ulli,int> mp; 111 queue<pair<Statement,int> > q; 112 ulli tar; 113 int ans; 114 115 inline void extend(const Statement &x,const int step) { 116 Statement nxt = x; 117 int tops[3]; 118 x.findtop(tops); 119 for(int i=0;i<3;i++) 120 for(int j=0;j<3;j++) 121 if( i != j && tops[j] < tops[i]) { // move from i to j . 122 nxt.s[i][tops[i]] = 0 , nxt.s[j][tops[i]] = 1; 123 ulli h = nxt.h(); 124 if( h == tar ) { 125 ans = step + 1; 126 return; 127 } else if( !mp.count(h) ) { 128 mp[h] = step + 1; 129 q.push(make_pair(nxt,step+1)); 130 } 131 nxt.s[i][tops[i]] = 1 , nxt.s[j][tops[i]] = 0; 132 } 133 } 134 135 int main() { 136 ans = -1; 137 if( n <= 15 ) { 138 for(int i=0,t,x;i<3;i++) { 139 scanf("%d",&t); 140 while(t--) scanf("%d",&x) , st.s[i][x] = 1; 141 } 142 ulli h = st.h(); 143 for(int i=0,t,x;i<3;i++) { 144 scanf("%d",&t); 145 while(t--) scanf("%d",&x) , ed.s[i][x] = 1; 146 } 147 tar = ed.h(); 148 q.push(make_pair(st,0)) , mp[h] = 0; 149 while( q.size() && !~ans ) { 150 extend(q.front().first,q.front().second) , q.pop(); 151 } 152 if( h == tar ) return puts("0"),0; 153 printf("%d\n",ans); 154 } else { 155 int ans = 1; 156 while(n--) ans = (long long) ans * 2 % 998244353; 157 ans = ( ans - 1 + 998244353 ) % 998244353; 158 printf("%d\n",ans); 159 } 160 return 0; 161 } 162 } 163 164 int main() { 165 scanf("%d",&n); 166 if( n <= 15 ) Force::main(); 167 else Sol::main(); 168 return 0; 169 }
稍加修改的60分代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<bitset> 6 #include<map> 7 #include<queue> 8 #define lli long long int 9 #define ulli unsigned long long 10 #define debug cout 11 using namespace std; 12 const int maxn=1e6+1e2,mod=998244353; 13 const int base=17; 14 const int maxl=20; 15 16 int n; 17 18 namespace Sol { 19 int st[3][maxn],ed[3][maxn],now[3][maxn]; 20 lli pows[maxn]; 21 22 inline int findmx(int sou[3][maxn]) { 23 int ret = -1; 24 for(int i=0;i<3;i++) 25 if( sou[i][0] && ( ret == -1 || sou[i][sou[i][0]] < sou[ret][sou[ret][0]] ) ) ret = i; 26 return ret; 27 } 28 inline int solve_merge(int siz,int tar) { 29 int xp = findmx(st); 30 while( siz && xp == tar ) st[xp][st[xp][0]] = 0 , st[xp][0]-- , siz-- , xp = findmx(st); 31 if( !siz ) return 0; 32 st[xp][st[xp][0]] = 0 , st[xp][0]--; 33 const int nt = 3 - xp - tar; 34 return ( solve_merge(siz-1,nt) + 1 + pows[siz-1] ) % mod; 35 } 36 37 inline void solve() { 38 int ms,me,siz=n; 39 lli ans = 0; 40 while( siz ) { 41 ms = findmx(st) , me = findmx(ed); 42 //debug<<"ms = "<<ms<<"me = "<<me<<endl; 43 if( ms == me ) { 44 st[ms][st[ms][0]] = 0 , --st[ms][0]; 45 ed[me][ed[me][0]] = 0 , --ed[me][0]; 46 --siz; 47 } else break; 48 } 49 if( !siz ) { 50 puts("0"); 51 return; 52 } 53 int ftar = 3 - ms - me; 54 st[ms][st[ms][0]] = 0 , --st[ms][0]; 55 ed[me][ed[me][0]] = 0 , --ed[me][0]; 56 --siz; 57 ans = solve_merge(siz,ftar) + 1; 58 //debug<<"inital ans = "<<ans<<endl; 59 while( siz ) { 60 while( siz && ( me = findmx(ed) ) == ftar ) { 61 ed[me][ed[me][0]] = 0 , --ed[me][0]; 62 --siz; 63 } 64 if( !siz ) break; 65 ans = ( ans + pows[siz-1] + 1 ) % mod; 66 ftar = 3 - me - ftar; 67 ed[me][ed[me][0]] = 0 , --ed[me][0] , --siz; 68 } 69 ans = ( ans + mod ) % mod; 70 printf("%lld\n",ans); 71 } 72 int main() { 73 for(int i=1;i<=n;i++) pows[i] = ( ( pows[i-1] << 1 ) | 1 ) % mod; 74 for(int i=0;i<3;i++) { 75 scanf("%d",st[i]); 76 for(int j=1;j<=st[i][0];j++) scanf("%d",st[i]+j) , st[i][j] = n - st[i][j] + 1; 77 //reverse(st[i]+1,st[i]+1+st[i][0]); 78 } 79 for(int i=0;i<3;i++) { 80 scanf("%d",ed[i]); 81 for(int j=1;j<=ed[i][0];j++) scanf("%d",ed[i]+j) , ed[i][j] = n - ed[i][j] + 1; 82 //reverse(ed[i]+1,ed[i]+1+ed[i][0]); 83 } 84 solve(); 85 return 0; 86 } 87 } 88 89 namespace Force { 90 struct Statement { 91 bitset<maxl> s[3]; 92 inline ulli h() const { 93 ulli ret = 0; 94 for(int i=0;i<3;i++) 95 for(int j=1;j<=n;j++) 96 ret = ret * base + ( j * s[i][j] ); 97 return ret; 98 } 99 inline void findtop(int* ret) const { 100 for(int i=0;i<3;i++) { 101 ret[i] = 0; 102 for(int j=n;j;j--) 103 if( s[i][j] ) { 104 ret[i] = j; 105 break; 106 } 107 } 108 } 109 }st,ed; 110 111 map<ulli,int> mp; 112 queue<pair<Statement,int> > q; 113 ulli tar; 114 int ans; 115 116 inline void extend(const Statement &x,const int step) { 117 Statement nxt = x; 118 int tops[3]; 119 x.findtop(tops); 120 for(int i=0;i<3;i++) 121 for(int j=0;j<3;j++) 122 if( i != j && tops[j] < tops[i]) { // move from i to j . 123 nxt.s[i][tops[i]] = 0 , nxt.s[j][tops[i]] = 1; 124 ulli h = nxt.h(); 125 if( h == tar ) { 126 ans = step + 1; 127 return; 128 } else if( !mp.count(h) ) { 129 mp[h] = step + 1; 130 q.push(make_pair(nxt,step+1)); 131 } 132 nxt.s[i][tops[i]] = 1 , nxt.s[j][tops[i]] = 0; 133 } 134 } 135 136 int main() { 137 ans = -1; 138 if( n <= 15 ) { 139 for(int i=0,t,x;i<3;i++) { 140 scanf("%d",&t); 141 while(t--) scanf("%d",&x) , st.s[i][n-x+1] = 1; 142 } 143 ulli h = st.h(); 144 for(int i=0,t,x;i<3;i++) { 145 scanf("%d",&t); 146 while(t--) scanf("%d",&x) , ed.s[i][n-x+1] = 1; 147 } 148 tar = ed.h(); 149 q.push(make_pair(st,0)) , mp[h] = 0; 150 while( q.size() && !~ans ) { 151 extend(q.front().first,q.front().second) , q.pop(); 152 } 153 if( h == tar ) return puts("0"),0; 154 printf("%d\n",ans); 155 } else { 156 int ans = 1; 157 while(n--) ans = (long long) ans * 2 % 998244353; 158 ans = ( ans - 1 + 998244353 ) % 998244353; 159 printf("%d\n",ans); 160 } 161 return 0; 162 } 163 } 164 165 int main() { 166 scanf("%d",&n); 167 if( n < 15 ) Force::main(); 168 else Sol::main(); 169 return 0; 170 }
考后AC代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #define lli long long int 6 using namespace std; 7 const int maxn=1e6+1e2; 8 const int mod=998244353; 9 10 int st[maxn],ed[maxn],way1[maxn],way2[maxn]; 11 lli ans; 12 13 inline void calc(int* dst,const int* sou,int pos,int tar) { 14 if( !pos ) return; 15 if( sou[pos] == tar ) return calc(dst,sou,pos-1,tar); 16 ++dst[pos-1] , calc(dst,sou,pos-1,6-tar-sou[pos]); 17 } 18 inline void fix(int* dst,int len) { 19 for(int i=0;i<len;i++) 20 dst[i+1] += dst[i] >> 1 , dst[i] &= 1; 21 } 22 inline bool cmp(int* lhs,int* rhs,int len) { 23 for(int i=len;~i;i--) if( lhs[i] != rhs[i] ) return lhs[i] < rhs[i]; 24 return 0; 25 } 26 inline lli getans(int* sou,int len) { 27 lli ret = 0; 28 for(int i=len;~i;i--) ret = ( ( ret << 1 ) + sou[i] ) % mod; 29 return ret; 30 } 31 32 int main() { 33 static int n,siz; 34 scanf("%d",&n),siz=n; 35 for(int i=1,p,x;i<=3;i++) { 36 scanf("%d",&p); 37 while(p--) scanf("%d",&x) , st[x] = i; 38 } 39 for(int i=1,p,x;i<=3;i++) { 40 scanf("%d",&p); 41 while(p--) scanf("%d",&x) , ed[x] = i; 42 } 43 while( st[siz] == ed[siz] ) --siz; 44 if( !siz ) return puts("0"),0; 45 calc(way1,st,siz-1,6-st[siz]-ed[siz]) , calc(way1,ed,siz-1,6-st[siz]-ed[siz]) , ++*way1; 46 calc(way2,st,siz-1,ed[siz]) , calc(way2,ed,siz-1,st[siz]) , ++*way2 , ++way2[siz-1]; 47 fix(way1,n+3) , fix(way2,n+3); 48 ans = cmp(way1,way2,n+3) ? getans(way1,n+3) : getans(way2,n+3); 49 printf("%lld\n",ans); 50 return 0; 51 }
T3:


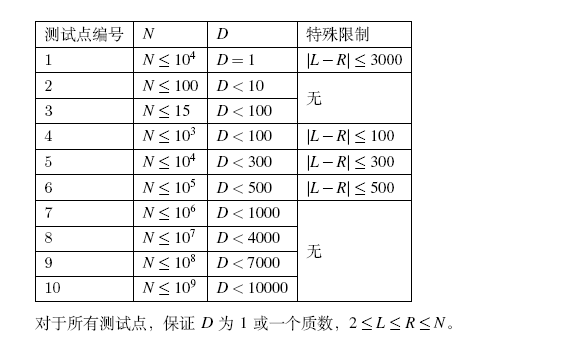
这一看就是神仙题啊,这东西人干事?
以下是官方的题解:



看不懂题解的我只好写了一个60分大力反演,弃坑了。
60分代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 #define lli long long int 7 #define debug cout 8 using namespace std; 9 const int maxn=1e6+1e2; 10 const int mod=998244353; 11 12 int bas[maxn],tim[maxn],mu[maxn]; 13 int n,D,L,R; 14 15 inline lli fastpow(lli base,int tim) { 16 lli ret = 1; 17 while( tim ) { 18 if( tim & 1 ) ret = ret * base % mod; 19 if( tim >>= 1 ) base = base * base % mod; 20 } 21 return ret % mod; 22 } 23 inline int gcd(int x,int y) { 24 if( ! ( x && y ) ) return x | y; 25 register int t; 26 while( ( t = x % y ) ) 27 x = y , y = t; 28 return y; 29 } 30 31 inline void pre() { 32 bas[1] = tim[1] = 1; 33 for(int i=2;i<=n;i++) { 34 if( !bas[i] ) for(lli j=i,cnt=1;j<=n;j*=i,++cnt) bas[j] = i , tim[j] = cnt; 35 } 36 } 37 inline void sieve() { 38 static int prime[maxn],cnt; 39 static char vis[maxn]; 40 mu[1] = 1; 41 for(int i=2;i<=n;i++) { 42 if( !vis[i] ) prime[++cnt] = i , mu[i] = -1; 43 for(int j=1;j<=cnt&&(lli)i*prime[j]<=n;j++) { 44 const int tar = i * prime[j]; 45 vis[tar] = 1; 46 if( ! ( i % prime[j]) ) break; 47 mu[tar] = -mu[i]; 48 } 49 } 50 } 51 52 inline lli force_g(int x,int sqt) { 53 int g = gcd( sqt , tim[x] ); 54 return fastpow(fastpow(bas[x],tim[x]/g),sqt/g); 55 } 56 inline lli force(int x) { 57 lli ret = 0; 58 const int lim = (int) ( log2(x) * D + 1e-6 ); 59 for(int i=D;i<=lim;i+=D) { 60 for(int j=1;j*i<=lim;j++) 61 ret += mu[i/D] * mu[j] * fastpow(j,D) * force_g(x,i*j) % mod , 62 ret %= mod; 63 } 64 return ret; 65 } 66 67 int main() { 68 static lli ans; 69 scanf("%d%d%d%d",&n,&D,&L,&R) , pre() , sieve(); 70 for(int i=L;i<=R;i++) ( ans += force(i) ) %= mod; 71 ans = ( ans % mod + mod ) % mod; 72 printf("%lld\n",ans); 73 return 0; 74 }
然后把神仙写的标程丢上来好了,反正我已经凉了。
神仙题的std:

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 typedef long long lint; 5 typedef long double db; 6 const int N = 500010, MO = 998244353; 7 8 inline int add(int a,int b) { return (a+b)%MO; } 9 inline int mul(int a,int b) { return (lint)a*b%MO; } 10 inline int powmod(int a,int b) 11 { 12 int s = 1; 13 for(;b;b>>=1,a=mul(a,a)) if(b&1) s = mul(s,a); 14 return s; 15 } 16 17 int n,D,L,R; 18 int sk[N],mu[N],c[N],pr[N],np[N],ps; 19 20 void pre() 21 { 22 int i,j; np[1] = 1, mu[1] = 1; 23 for(i=2;i<N;i++) 24 { 25 if(!np[i]) pr[++ps] = i, mu[i] = MO-1; 26 for(j=1;j<=ps&&i*pr[j]<N;j++) 27 { 28 np[i*pr[j]] = 1; 29 if(i%pr[j]==0) break; 30 mu[i*pr[j]] = (MO-mu[i])%MO; 31 } 32 } 33 for(i=1;i<=33;i++) 34 { 35 for(j=1;j<=i;j++) if(i%j==0) 36 c[i] = add(c[i],mul(mul(mu[j],mu[i/j]),powmod(i/j,D))); 37 } 38 } 39 40 int sum(int k,int l,int r) 41 { 42 if(l>r) return 0; 43 k++; 44 int s = 0, top = min(k,r); 45 int i,j; 46 sk[1] = 1; 47 for(i=2;i<=top;i++) 48 { 49 if(!np[i]) sk[i] = powmod(i,k-1); 50 for(j=1;j<=ps&&pr[j]<=i&&i*pr[j]<=top;j++) 51 { 52 sk[i*pr[j]] = mul(sk[i],sk[pr[j]]); 53 if(i%pr[j]==0) break; 54 } 55 } 56 if(r<=k) 57 { 58 for(int i=l;i<=r;i++) 59 s = add(s,sk[i]); 60 return s; 61 } 62 for(i=1;i<=k;i++) sk[i] = add(sk[i],sk[i-1]); 63 static int fc[N],iv[N],ml[N],mr[N]; 64 fc[0] = 1, ml[0] = 1, mr[k] = 1; 65 for(i=1;i<=k;i++) fc[i] = mul(fc[i-1],i), ml[i] = mul(ml[i-1],r-k+i-1); 66 iv[k] = powmod(fc[k],MO-2); 67 for(i=k-1;i>=0;i--) mr[i] = mul(mr[i+1],r-k+i+1), iv[i] = mul(iv[i+1],i+1); 68 for(i=0;i<=k;i++) s = add(s,(MO+(i&1?-1:1)*mul(sk[k-i],mul(mul(ml[i],mr[i]),mul(iv[i],iv[k-i]))))%MO); 69 70 l--; 71 for(i=1;i<=k;i++) ml[i] = mul(ml[i-1],l-k+i-1); 72 for(i=k-1;i>=0;i--) mr[i] = mul(mr[i+1],l-k+i+1); 73 for(i=0;i<=k;i++) s = add(s,(MO-(i&1?-1:1)*mul(sk[k-i],mul(mul(ml[i],mr[i]),mul(iv[i],iv[k-i]))))%MO); 74 return s; 75 } 76 77 inline int rtceil(int a,int b) 78 { 79 int x = pow(a,1/(db)b); 80 while(pow(x,b)>a) x--; 81 while(pow(x,b)<a) x++; 82 return x; 83 } 84 85 inline int rtfloor(int a,int b) 86 { 87 int x = pow(a,1/(db)b); 88 while(pow(x,b)<a) x++; 89 while(pow(x,b)>a) x--; 90 return x; 91 } 92 93 int calcg(int m) 94 { 95 int s = 0; 96 for(int k=1;k<=m;k++) if(m%k==0) 97 { 98 int x = max(rtceil(L,k),(int)ceil(pow(2,m/k/(db)D))); 99 int y = rtfloor(R,k); 100 s = add(s,sum(m/k,x,y)); 101 } 102 for(int l=2;l<=m;l++) if(m%l==0&&mu[l]) 103 { 104 int t = 0; 105 for(int k=1;k*l<=m;k++) if(m%(k*l)==0) 106 { 107 int _l = max((int)ceil(pow(2,m/(k*l)/(db)D)),rtceil(L,k*l)); 108 int _r = rtfloor(R,k*l); 109 t = add(t,sum(m/k*l,_l,_r)); 110 } 111 s = add(s,mul(t,mu[l])); 112 } 113 return s; 114 } 115 116 int work() 117 { 118 int s = 0; 119 pre(); 120 for(lint m=D,p=2;p<=R;m+=D,p<<=1) 121 s = add(s,mul(c[m/D],calcg(m))); 122 return s; 123 } 124 125 int main() 126 { 127 scanf("%d%d%d%d",&n,&D,&L,&R); 128 printf("%d\n",work()); 129 return 0; 130 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号