Bzoj2694/Bzoj4659:莫比乌斯反演
Bzoj2694/Bzoj4659:莫比乌斯反演
先上题面:
首先看到这数据范围显然是反演了,然而第三个限制条件十分不可做。于是我们暂且无视他,大不了补集转化算完再减是吧。
于是我们有: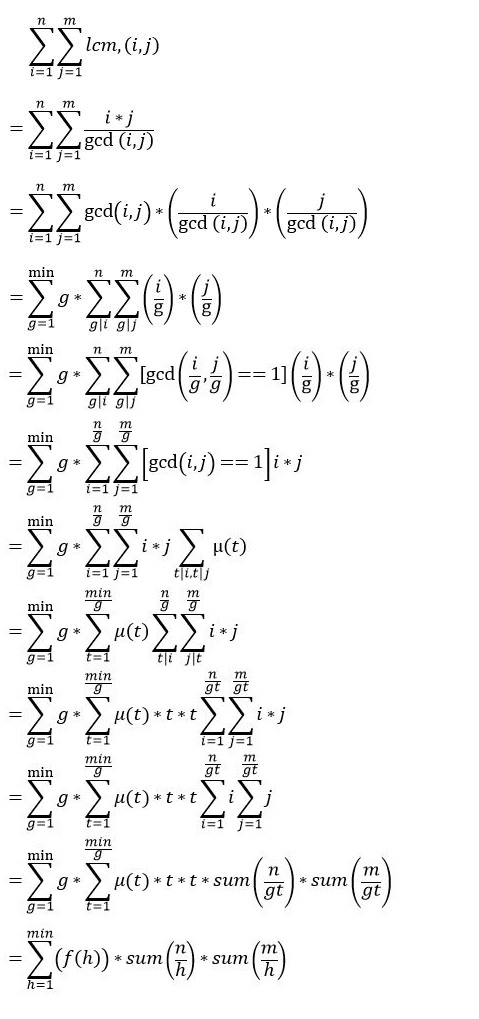
这里我们定义: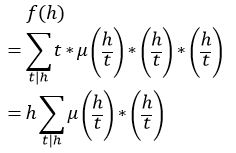
于是这个东西我们可以nlogn筛的说。
也就是说,我们求出f的前缀和后,就可以O(sqrt(n)+sqrt(m))分块计算了。
然而需要减去的东西怎么办呢?
反演题最难的不是推公式,而是你推出了公式却不知道是否可做。
仔细观察以上两个式子,原式中的g(也就是上式中的t),不就是我们枚举的gcd吗?
题面要求两个数不同时含某个平方因数,也就是他们的gcd不同时含某个平方因数。
那不就是我们原式中的g(上式中的t)不含平方因数吗?
而一个数x含平方因数,会有什么性质呢?μ(x)=0!
所以我们先枚举t,判断其μ值非0,然后去枚举h/t,更新f(h)即可。
这题取模2^30,我们直接用int自然溢出就好了。
(为什么?因为这样加减乘显然是对的,然而除法,只有在计算sum的时候会除二,这样我们会损失一位的精度。而int的正数精度为取模2^31的,损失一位后正好够用,所以我们可以这样做。理论上取模2^31我们也可以用unsigned int做,然而取模2^32就必须long long了。以上内容纯属口胡,如果因此wa了别打我就是了QAQ……)
代码:
(一开始sieve里面开的数组没加static wa了一次,身败名裂)

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #define lli long long int 6 #define debug cout 7 using namespace std; 8 const int maxn=4e6+1e2,lim=4e6; 9 const int mod = 1 << 30; 10 11 int mu[maxn],f[maxn]; 12 13 inline void sieve() { 14 static int prime[maxn],cnt; 15 static bool vis[maxn]; 16 mu[1] = 1; 17 for(int i=2;i<=lim;i++) { 18 if( !vis[i] ) prime[++cnt] = i , mu[i] = -1; 19 for(int j=1;j<=cnt&&(lli)i*prime[j]<=lim;j++) { 20 const int tar = i * prime[j]; 21 vis[tar] = 1; 22 if( ! ( i % prime[j] ) ) break; 23 mu[tar] = -mu[i]; 24 } 25 } 26 for(int i=1;i<=lim;i++) if( mu[i] ) { 27 for(int j=1;(lli)i*j<=lim;j++) f[i*j] += j * mu[j]; 28 } 29 for(int i=1;i<=lim;i++) f[i] *= i , f[i] += f[i-1]; 30 } 31 inline int sum(int x) { 32 return x * ( x + 1 ) >> 1; 33 } 34 inline int calc(int n,int m) { 35 if( n > m ) swap(n,m); 36 int ret = 0; 37 for(int l=1,r;l<=n;l=r+1) { 38 r = min( n / ( n / l ) , m / ( m / l ) ); 39 ret += ( f[r] - f[l-1] ) * sum(n/l) * sum(m/l); 40 } 41 return ret; 42 } 43 44 int main() { 45 static int T,a,b; 46 static lli ans; 47 scanf("%d",&T) , sieve(); 48 while(T--) { 49 scanf("%d%d",&a,&b) , ans = calc(a,b); 50 ans = ( ans % mod + mod ) % mod; 51 printf("%lld\n",ans); 52 } 53 return 0; 54 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号