20180222小测
今天又是猝不及防的一场考试。
我赶紧去打卡,于是get:参加模拟赛,爆零。

T1:

这不是秦神上次的原题吗?赶紧粘一发代码走了(不)。

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<vector> 6 #include<queue> 7 #define debug cout 8 using namespace std; 9 const int maxn=2e2+1e1,maxm=4e4+1e2,maxe=55; 10 const int inf=0x3f3f3f3f; 11 12 int k[maxn],sum[maxn],n,full,mip,ans; 13 int st,ed,len; 14 bool vis[maxn]; 15 16 struct Elevator { 17 int h,x,y; 18 friend bool operator < (const Elevator &a,const Elevator &b) { 19 if( a.h != b.h ) return a.h < b.h; 20 if( a.x != b.x ) return a.x < b.x; 21 return a.y < b.y; 22 } 23 friend bool operator == (const Elevator &a,const Elevator &b) { 24 return a.h == b.h && a.x == b.x && a.y == b.y; 25 } 26 }; 27 vector<Elevator> v; 28 29 namespace Flow { 30 int s[maxn],t[maxm<<1],nxt[maxm<<1],f[maxm<<1],dep[maxn],cnt=1; 31 32 inline void coredge(int from,int to,int flow) { 33 t[++cnt] = to , f[cnt] = flow , 34 nxt[cnt] = s[from] , s[from] = cnt; 35 } 36 inline void singledge(int from,int to,int flow) { 37 coredge(from,to,flow) , coredge(to,from,0); 38 } 39 inline bool bfs() { 40 memset(dep,-1,sizeof(dep)) , dep[st] = 0; 41 queue<int> q; q.push(st); 42 while( q.size() ) { 43 const int pos = q.front(); q.pop(); 44 for(int at=s[pos];at;at=nxt[at]) { 45 if( f[at] && !~dep[t[at]] ) dep[t[at]] = dep[pos] + 1 , q.push(t[at]); 46 } 47 } 48 return ~dep[ed]; 49 } 50 inline int dfs(int pos,int flow) { 51 if( pos == ed ) return flow; 52 int ret = 0 , now = 0; 53 for(int at=s[pos];at;at=nxt[at]) 54 if( f[at] && dep[t[at]] > dep[pos] ) { 55 now = dfs(t[at],min(flow,f[at])); 56 ret += now , flow -= now , 57 f[at] -= now , f[at^1] += now; 58 if( !flow ) return ret; 59 } 60 if( !ret ) dep[pos] = -1; 61 return ret; 62 } 63 inline int dinic() { 64 int ret = 0 , now = 0; 65 while( bfs() ) 66 while( ( now = dfs(st,inf) ) ) ret += now; 67 return ret; 68 } 69 inline void reset() { 70 memset(s,0,sizeof(s)) , cnt = 1; 71 } 72 } 73 74 inline int countbit(int x) { 75 #define lowbit(x) (x&-x) 76 int ret = 0; 77 while( x ) ++ret , x -= lowbit(x); 78 return ret; 79 } 80 inline int covdep(int dep,int pos) { 81 return sum[dep-1] + pos; 82 } 83 84 inline int rebuild(int sta) { 85 Flow::reset() , memset(vis,0,sizeof(vis)); 86 int ret = 0; 87 for(int i=0;i<k[mip];i++) if( ! ( sta & ( 1 << i ) ) ) vis[covdep(mip,i+1)] = 1; 88 for(int i=0;i<len;i++) { 89 const int h = v[i].h , th = h != n ? h + 1 : 1; 90 if( h == mip) { 91 if( ( 1 << ( v[i].x - 1 ) ) & sta ) vis[covdep(th,v[i].y)] = 1; 92 } 93 else if( th == mip ) { 94 if( ( 1 << ( v[i].y - 1 ) ) & sta ) vis[covdep(h,v[i].x)] = 1; 95 }else { 96 if( ( h > mip && ( ( h - mip ) & 1 ) ) || ( h < mip && ! ( ( mip - h ) & 1 ) ) ) 97 Flow::singledge(covdep(h,v[i].x),covdep(th,v[i].y),1); 98 else Flow::singledge(covdep(th,v[i].y),covdep(h,v[i].x),1); 99 } 100 } 101 for(int i=1;i<=n;i++) { 102 if( ( i > mip && ( ( i - mip ) & 1 ) ) || ( i < mip && !( ( mip - i ) & 1 ) ) ) { 103 for(int j=1;j<=k[i];j++) 104 if( !vis[covdep(i,j)] ) Flow::singledge(st,covdep(i,j),1); 105 } else if( i != mip ) { 106 for(int j=1;j<=k[i];j++) 107 if( !vis[covdep(i,j)] ) Flow::singledge(covdep(i,j),ed,1); 108 } 109 } 110 for(int i=1;i<=full;i++) ret += !vis[i]; 111 ret -= Flow::dinic(); 112 return ret; 113 } 114 inline void getansodd() { 115 int fs = ( 1 << k[mip] ); 116 for(int i=0;i<fs;i++) ans = max( ans , rebuild(i) ); 117 } 118 inline void getanseven() { 119 for(int i=0;i<len;i++) { 120 const int x = covdep(v[i].h,v[i].x); 121 const int y = covdep(v[i].h!=n?v[i].h+1:1,v[i].y); 122 if( v[i].h & 1 ) Flow::singledge(x,y,1); 123 else Flow::singledge(y,x,1); 124 } 125 for(int i=1;i<=n;i++) { 126 if( i & 1 ) { 127 for(int j=1;j<=k[i];j++) 128 Flow::singledge( st , covdep(i,j) , 1 ); 129 } else { 130 for(int j=1;j<=k[i];j++) 131 Flow::singledge( covdep(i,j) , ed , 1 ); 132 } 133 } 134 ans = full - Flow::dinic(); 135 } 136 137 inline void pre() { 138 sort(v.begin(),v.end()); 139 len = unique(v.begin(),v.end()) - v.begin(); 140 for(int i=1;i<=n;i++) sum[i] = sum[i-1] + k[i]; 141 full = sum[n] , st = full + 1 , ed = full + 2; 142 *k = inf; 143 for(int i=1;i<=n;i++) if( k[i] < k[mip] ) mip = i; 144 } 145 146 int main() { 147 static int h,x,y; 148 scanf("%d",&n); 149 int t = 0; 150 while( scanf("%d%d%d",&x,&y,&h) == 3 ) { 151 v.push_back((Elevator){h,x,y}); 152 k[h] = max( k[h] , x ) , k[h!=n?h+1:1] = max( k[h!=n?h+1:1] , y ); 153 ++t; 154 } 155 pre(); 156 if( n & 1 ) getansodd(); 157 else getanseven(); 158 printf("%d\n",ans); 159 return 0; 160 }
T2:
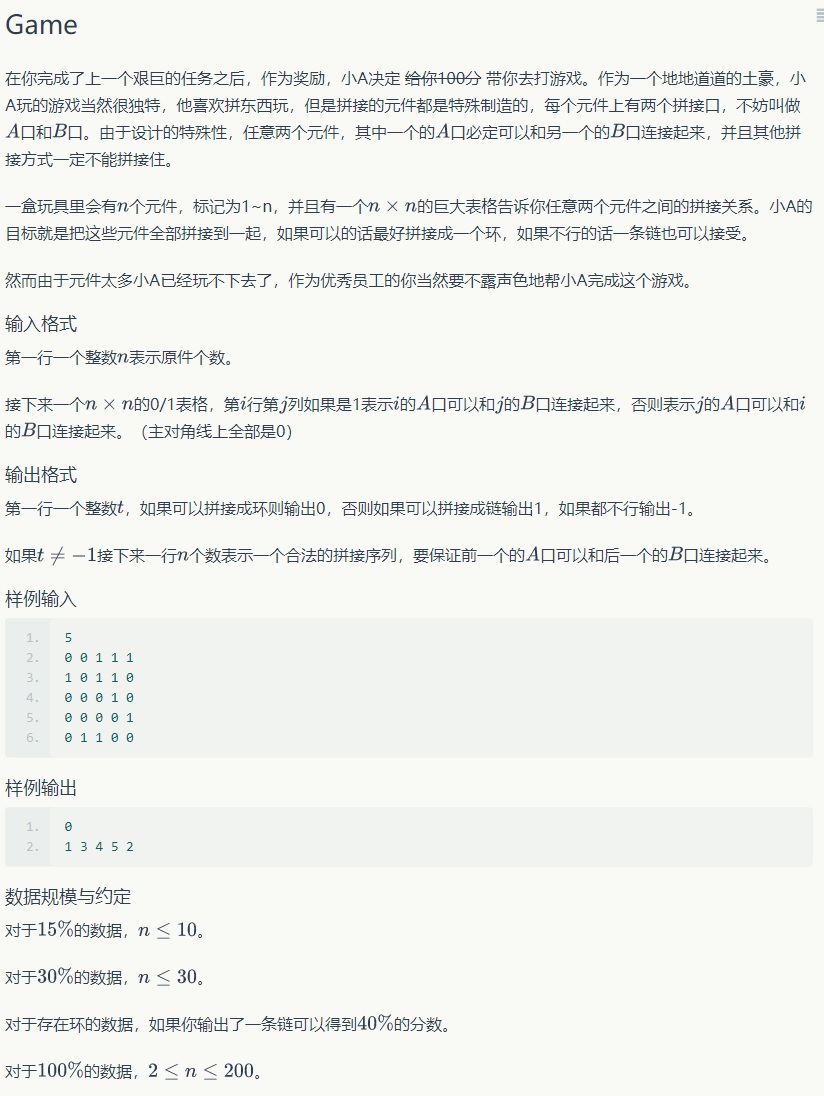
让你找一个长度为n的简单环或链并输出方案。
首先先考虑环是否存在的问题,随便乱搞一下看有没有长为n的简单路径就行了,等等,这东西能搞?30分钟过去了。
有没有环?tarjan一发看看所有点是否在一个强连通里不就行了……
输出方案,这东西怎么办?
手玩了多种方案发现无解后,我开始考虑弃疗。
这不是哈密顿回路吗?这不NP吗?woc这玩意能做?
n<=10的15分枚举全排列就好,n<=30的15分大概给什么随机化了吧(写了也不一定有分,不写了QAQ)。
n<=200,最短路乱搞骗分得了。
等会,这是二分图?然而二分图有一堆小环怎么办啊,弃了弃了。
--------我是废话的分割线--------
其实这种图是一张竞赛图,我们能够通过归纳法证明这张图中一定存在哈密顿通路。
怎么证?考虑2个点的初始情况一定可行,那么我们要用归纳法证明在n个点可行的情况下n+1个点也可行。
如果新加进来的点只有出边或只有入边,那么我们把他放到尾就好了。
考虑序列中的每一个位置,如果新加的点有顺序边(原来序列a->b新加点x,我们有a->x,x->b的边),我们直接把新加点x加入就行。
否则,则新加点有且仅有逆序边,由于逆序边这种东西不可连续,则新加点x一定向序列前一段的点连出边,被序列后一段的点连入边(脑补一下),这样我们就可以把x放在头或者尾了。
所以我们证明了,n>=2的竞赛图一定有哈密顿通路。
关于环(哈密顿回路)的问题,Dirac定理告诉我们顶点的度数大于等于N/2,则哈密顿回路一定存在,同时鸽巢原理告诉我们如果一张竞赛图所有点在同一个强连通分量中,则一定存在哈密顿回路(别问我怎么证明),然后就是构造的问题。
构造的话,我们可以枚举初始点,然后加点,构造出没有重复点的最长链。最后是不是环就听天由命吧。(某神奇定理告诉我们只要枚举所有初始点则能构造出环)。
看成绩时发现,直接无脑匈牙利输出方案有55分,dinic输出方案能A(天知道这数据怎么回事)。
考场25分代码:

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #define debug cout 5 #include<iostream> 6 using namespace std; 7 const int maxn=4e2+1e1; 8 const int inf=0x3f3f3f3f; 9 10 int in[maxn][maxn]; 11 int n; 12 13 namespace Force { 14 int pts[maxn],ans[maxn],sta=-1; 15 inline int judge() { // return 0 if it is a ring , 1 if it is a chain . 16 for(int i=1;i<n;i++) 17 if( !in[pts[i]][pts[i+1]] ) return -1; 18 return 1 - in[pts[n]][pts[1]]; 19 } 20 inline void work() { 21 for(int i=1;i<=n;i++) pts[i] = i; 22 do { 23 int t = judge(); 24 if( t == 0 ) { 25 sta = 0 , memcpy(ans+1,pts+1,sizeof(int)*n); 26 break; 27 } else if( t == 1 && !~sta ) { 28 sta = 1 , memcpy(ans+1,pts+1,sizeof(int)*n); 29 } 30 } while( std::next_permutation(pts+1,pts+1+n) ); 31 printf("%d\n",sta); 32 if( ~sta ) for(int i=1;i<=n;i++) printf("%d%c",ans[i],i!=n?' ':'\n'); 33 } 34 } 35 namespace Exp { 36 int dis[maxn][maxn]; 37 int ans[maxn],cnt,sta=-1,sx,sy; 38 inline void gen() { 39 for(int i=1;i<=n;i++) 40 for(int j=1;j<=n;j++) { 41 dis[i][j] = -inf; 42 if( in[i][j] ) dis[i][j] = 1; 43 } 44 } 45 inline void floyd() { 46 for(int k=1;k<=n;k++) 47 for(int i=1;i<=n;i++) 48 for(int j=1;j<=n;j++) { 49 if( i == k || j == k ) continue; 50 if( dis[i][j] < dis[i][k] + dis[k][j] ) { 51 dis[i][j] = dis[i][k] + dis[k][j]; 52 } 53 } 54 } 55 inline void getans() { 56 for(int i=1;i<=n;i++) 57 if( dis[i][i] == n ) { 58 sta = 0 , sx = i; 59 return; 60 } 61 for(int i=1;i<=n;i++) 62 for(int j=1;j<=n;j++) 63 if( dis[i][j] == n - 1 ) { 64 sta = 1 , sx = i; 65 return; 66 } 67 } 68 int t = 0; 69 inline void work() { 70 gen() , floyd() , getans(); 71 if( ~sta ) { 72 for(int i=1;i<=n;i++) ans[dis[sx][i]%n] = i; 73 printf("%d\n",sta); 74 for(int i=0;i<n;i++) printf("%d ",ans[i]); 75 } 76 } 77 } 78 79 int main() { 80 scanf("%d",&n); 81 for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) scanf("%d",&in[i][j]); 82 if( n <= 15 ) Force::work(); 83 else Exp::work(); 84 fclose(stdout); 85 return 0; 86 }
考后AC代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #define debug cout 6 using namespace std; 7 const int maxn=2e2+1e1; 8 9 int in[maxn][maxn],ans[maxn]; 10 int n,tpe; 11 12 namespace Tarjan { 13 int dfn[maxn],low[maxn],id[maxn],stk[maxn],vis[maxn],ins[maxn],top,dd,iid; 14 inline void dfs(int pos) { 15 vis[pos] = 1; 16 low[pos] = dfn[pos] = ++dd , 17 stk[++top] = pos , ins[pos] = 1; 18 for(int i=1;i<=n;i++) 19 if( in[pos][i] && !vis[i] ) { 20 dfs(i); 21 low[pos] = min( low[pos] , low[i] ); 22 } else if( ins[i] ) low[pos] = min( low[pos] , dfn[i] ); 23 if( low[pos] == dfn[pos] ) { 24 ++iid; 25 do { 26 const int x = stk[top--]; ins[x] = 0; 27 id[x] = iid; 28 } while( ins[pos] ); 29 } 30 } 31 inline bool work() { 32 for(int i=1;i<=n;i++) if( !vis[i] ) dfs(i); 33 for(int i=1;i<=n;i++) if( id[i] != id[1] ) return 0; 34 return 1; 35 } 36 } 37 namespace Build { 38 int nxt[maxn],used[maxn],head,tail; 39 inline void init(int hh) { 40 memset(nxt,0,sizeof(nxt)); 41 head = tail = hh; 42 } 43 inline int build(int hh) { 44 init(hh); 45 for(int i=1;i<=n;i++) 46 if( i != hh ) { 47 if( in[i][head] ) nxt[i] = head , head = i; 48 else { 49 int now; 50 for(now=head;nxt[now]&&in[nxt[now]][i];now=nxt[now]); 51 nxt[i] = nxt[now] , nxt[now] = i; 52 if( !nxt[i] ) tail = i; 53 } 54 } 55 return in[tail][head]; 56 } 57 inline void getans(int tpe) { 58 if( tpe ) build(1); 59 else for(int i=1;i<=n;i++) if( build(i) ) break; 60 for(int i=head,now=0;i;i=nxt[i]) ans[++now] = i; 61 } 62 63 } 64 65 int main() { 66 scanf("%d",&n); 67 for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) scanf("%d",in[i]+j); 68 int tpe = Tarjan::work() ^ 1; 69 Build::getans(tpe); 70 printf("%d\n",tpe); 71 for(int i=1;i<=n;i++) printf("%d%c",ans[i],i!=n?' ':'\n'); 72 return 0; 73 }
T3:

全世界都知道这题是费用流(不),为什么只有我在想怎么dp?
考场写了30分爆搜,结果没开long long 10分滚粗啦!(你不告诉我数据范围怪我喽)
首先我们先钦定小A全程睡觉,我们设0/1变量xi为第i天睡觉是否改成吃饭。
然后我们就是要在符合要求的情况下让修改的代价尽可能小,也就是说最小费用最大流了。
关于要求,我们有:

我们全部加入变量y,补成等式:

关于y的范围:前n-k个为[0,n-ms-me],后
上下作差:
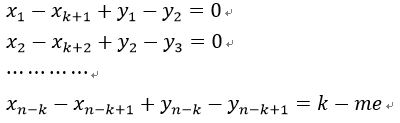
如果我们把每个方程看做点,x,y的加减看做边,x,y的范围看做流量,x,y改动的价值看做边权,这不就是费用流了呢?
关于数值细节自己推吧。
考场10分代码:

1 #include<cstdio> 2 #include<algorithm> 3 const int maxn=1e2+1e1; 4 5 int in[maxn][2],sta[maxn]; 6 int n,k,ms,me,ans; 7 8 inline void judge() { 9 int ss = 0 , se = 0 , sum = 0; 10 for(int i=1;i<k;i++) ss += sta[i] == 1 , se += sta[i] == 2 , sum += in[i][sta[i]-1]; 11 for(int i=k;i<=n;i++) { 12 ss += sta[i] == 1 , se += sta[i] == 2 , sum += in[i][sta[i]-1]; 13 ss -= sta[i-k] == 1 , se -= sta[i-k] == 2; 14 if( ss < ms || se < me ) return; 15 } 16 ans = std::max(ans,sum); 17 } 18 inline void dfs(int pos) { 19 if( pos > n ) return judge(); 20 sta[pos] = 1 , dfs(pos+1) , 21 sta[pos] = 2 , dfs(pos+1) ; 22 } 23 24 int main() { 25 scanf("%d%d%d%d",&n,&k,&ms,&me) , ans = -0x7fffffff; 26 for(int i=1;i<=n;i++) scanf("%d",in[i]); 27 for(int i=1;i<=n;i++) scanf("%d",in[i]+1); 28 dfs(1); 29 printf("%d\n",ans); 30 fclose(stdout); 31 return 0; 32 }
考后AC代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<queue> 6 #define lli long long int 7 #define debug cout 8 using namespace std; 9 const int maxn=1e3+1e2,maxe=maxn<<4; 10 const int int_inf=0x3f3f3f3f; 11 const lli lli_inf=0x3f3f3f3f3f3f3f3fll; 12 13 lli ins[maxn],ine[maxn]; 14 int s[maxn],t[maxe],nxt[maxe],f[maxe],sou[maxn]; 15 lli c[maxe],dis[maxn]; 16 bool inq[maxn]; 17 int n,k,ms,me,st,ed,lim; 18 19 inline void coredge(int from,int to,int flow,lli cost) { 20 static int cnt = 1; 21 t[++cnt] = to , f[cnt] = flow , c[cnt] = cost , 22 nxt[cnt] = s[from] , s[from] = cnt; 23 } 24 inline void singledge(int from,int to,int flow,lli cost) { 25 coredge(from,to,flow,cost) , coredge(to,from,0,-cost); 26 } 27 inline bool spfa() { 28 memset(dis,0x3f,sizeof(dis)) , dis[st] = 0; 29 queue<int> q; q.push(st) , inq[st] = 1; 30 while( q.size() ) { 31 const int pos = q.front(); q.pop() , inq[pos] = 0; 32 for(int at=s[pos];at;at=nxt[at]) 33 if( f[at] && dis[t[at]] > dis[pos] + c[at] ) { 34 dis[t[at]] = dis[pos] + c[at] , sou[t[at]] = at; 35 if( !inq[t[at]] ) q.push(t[at]) , inq[t[at]] = 1; 36 } 37 } 38 return dis[ed] != lli_inf; 39 } 40 inline int release() { 41 int ret = int_inf; 42 for(int i=ed;i!=st;i=t[sou[i]^1]) 43 ret = min( ret , f[sou[i]] ); 44 for(int i=ed;i!=st;i=t[sou[i]^1]) 45 f[sou[i]] -= ret , f[sou[i]^1] += ret; 46 return ret; 47 } 48 inline lli flow() { 49 lli ret = 0; 50 while( spfa() ) ret += dis[ed] * release(); 51 return ret; 52 } 53 54 int main() { 55 static lli ans; 56 scanf("%d%d%d%d",&n,&k,&ms,&me) , st = n + 1 , ed = n + 2; 57 for(int i=1;i<=n;i++) scanf("%lld",ins+i) ; // ine :: value we lost in chageing e into s . 58 for(int i=1;i<=n;i++) scanf("%lld",ine+i) , ans += ine[i] , ine[i] -= ins[i]; 59 lim = k - ms - me ; 60 61 singledge(st,1,lim,0) , singledge(n,ed,k-me,0); 62 for(int i=1;i<n;i++) singledge(i,i+1,i>=n-k+1?k-me:lim,0); 63 for(int i=1;i<=k;i++) singledge(st,i,1,ine[i]); 64 for(int i=1;i+k<=n;i++) singledge(i,i+k,1,ine[i+k]); 65 66 /*singledge(st,1,k-me,0) , singledge(n,ed,lim,0); 67 for(int i=1;i<n;i++) singledge(i,i+1,i<k?k-me:lim,0); 68 for(int i=1;i+k<=n;i++) singledge(i,i+k,1,ine[i]); 69 for(int i=n-k+1;i<=n;i++) singledge(i,ed,1,ine[i]);*/ 70 71 ans -= flow(); 72 printf("%lld\n",ans); 73 74 return 0; 75 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号