20180213小测
20180213小测
上了几天课后,我么迎来了秦神的考试……
上次秦神出题T1T3集体爆零的心里阴影还没有褪去QAQ……
T1:


说白了就是让你在原串中选出一些子串使之价值和最大,已经被删去的子串使得区间两端合并。
首先注意这题是子串而不是子序列。考试的时候我当子序列做了半天,什么贪心、DP、网络流全都试了一遍,发现根本不可做,连爆搜都不会写……
然而看到这题这样就肯定是区间DP了,因为我们选择的是一个子串,所以对于一个我们要选出的串,他要么在原串中连续出现,要么在原串中分开出现且间隔部分可以全部被选出。
所以我们令f[i][j][p][k]表示原串区间[i,j],匹配目标串p,第i位匹配第1位,第j维匹配第k位,dp[i][j]表示原串[i,j]能否被完全选出(先别管我为什么这么定义,一会看转移就明白了QAQ)。
我们考虑串p的位置k-1匹配的位置。我们在区间[I,j)枚举l,表示第k-1位匹配的位置。
若l==k-1,则中间没有间隔串,f[i][j][p][k]从f[i][l][p][k-1]转移。
若l!=k-1,说明中间间隔了一些部分且他们必须完全消去,所以我们让f[i][j][p][k]从f[i][l][p][k-1]&&dp[l+1][j]转移。
对于dp数组,一个能完全选出的区间要么由两边两个能完全选出的区间组成,要么恰好完美匹配某个目标串,我们枚举一下分割位置或者匹配的目标串即可。
复杂度?f的转移把[p][k]摊还下来是O(n^4)的,且为区间DP,有一个最大1/8的常数。dp的转移只用枚举中间位置或匹配串,复杂度O(n^3)。实测跑得飞快。
然而这题限制64mb内存,你直接开会MLE。用vector进行动态resize依旧会MLE(亲测还会TLE)。你需要开出f[i][j][p]的指针,最后一维k用C++的new分配内存就好了。
关于答案统计,我们可以看做在区间内选择几条有权值且不相同的线段覆盖,做线段覆盖就好了。
代码:

1 #include<cstdio> 2 #include<cstring> 3 #include<vector> 4 #define bool unsigned char 5 const int maxn=1e2+1e1,maxl=1.5e2+1e1; 6 7 char in[maxl],tar[maxn][maxl]; 8 int val[maxn],sum[maxl],lt[maxn],g[maxl]; 9 bool* f[maxl][maxl][maxn]; 10 bool dp[maxl][maxl]; 11 int n,li; 12 13 inline void getans() { 14 for(int len=1;len<=li;len++) 15 for(int st=1;st+len-1<=li;st++) { 16 const int ed = st + len - 1; 17 for(int p=1;p<=n;p++) { // p is the pairing string . 18 for(int k=1;k<=lt[p]&&k<=len;k++) { 19 if( in[ed] != tar[p][k] ) continue; 20 if( k == 1 ) { 21 if( st == ed ) f[st][ed][p][k] = 1; 22 else f[st][ed][p][k] = dp[st][ed-1]; 23 continue; 24 } 25 for(int l=st;l<ed;l++) { 26 if( l == ed - 1 ) f[st][ed][p][k] |= f[st][l][p][k-1]; 27 else f[st][ed][p][k] |= f[st][l][p][k-1] && dp[l+1][ed-1]; 28 } 29 } 30 } 31 for(int mid=st;mid<ed;mid++) 32 dp[st][ed] |= ( dp[st][mid] && dp[mid+1][ed] ); 33 for(int p=1;p<=n;p++) 34 dp[st][ed] |= f[st][ed][p][lt[p]]; 35 } 36 for(int i=0;i<=li;i++) { // g[i] is proccessed 37 if( i ) g[i] = std::max( g[i] , g[i-1] ); 38 for(int ed=i+1;ed<=li;ed++) 39 if( dp[i+1][ed] ) g[ed] = std::max( g[ed] , g[i] + sum[ed] - sum[i] ); 40 } 41 } 42 inline void readin() { 43 static int k,p; 44 static char s[maxl]; 45 scanf("%d",&k); 46 while( k-- ) { 47 scanf("%s%d",s,&p); 48 val[(int)*s-'a'] = p; 49 } 50 scanf("%s",in+1) , li = strlen(in+1); 51 for(int i=1;i<=li;i++) sum[i] = sum[i-1] + val[(int)in[i]-'a']; 52 scanf("%d",&n); 53 for(int i=1;i<=n;i++) { 54 scanf("%s",tar[i]+1); 55 lt[i] = strlen(tar[i]+1); 56 for(int j=1;j<=li;j++) 57 for(int k=1;k<=li;k++) { 58 f[j][k][i] = new bool [lt[i]+1]; 59 for(int p=0;p<=lt[i];p++) 60 f[j][k][i][p] = 0; 61 } 62 } 63 } 64 65 int main() { 66 readin(); 67 getans(); 68 printf("%d\n",g[li]); 69 return 0; 70 }
T2:

关于题意:如果若干个点全都距离很近能相互到达,使得能到达每家店的数量大于等于k,则全部关门。
我们把距离转成切比雪夫距离,那么一家店能到达的店在一个矩形内。我们只用统计出一家店能被多少家到达,就可以知道他是否需要关门。
二维数据结构随便做啊,然而64mb内存卡树套树,懒得调扫描线或分治。考虑n只有10w,分块的数据范围,所以好写好调的kdtree随便过啊。
我们对于每个节点记录这个节点被完整覆盖了多少遍,最后再把树dfs一遍好了。统计答案的时候别忘了减去自身对自身的贡献。
码了十几分钟考场一发AC,话说这题为什么就我一个拿分的?别人都写跪了?
代码:

1 #pragma GCC optimize(3) 2 #include<iostream> 3 #include<cstdio> 4 #include<cstring> 5 #include<algorithm> 6 #define lli long long int 7 #define debug cout 8 using namespace std; 9 const int maxn=1e5+1e2; 10 11 int cmp; 12 struct Point { 13 int d[2],id; // 0 means x , 1 means y . 14 friend bool operator < (const Point &a,const Point &b) { 15 return a.d[cmp] < b.d[cmp]; 16 } 17 }ps[maxn],nv[maxn]; 18 int lson[maxn],rson[maxn],mx[maxn][2],mi[maxn][2],lazy[maxn],cnt; 19 int inx[maxn],iny[maxn],ind[maxn],ans[maxn]; 20 21 inline void fill(int pos,const Point &p) { 22 nv[pos] = p; 23 for(int i=0;i<2;i++) 24 mx[pos][i] = mi[pos][i] = p.d[i]; 25 } 26 inline void update(int fa,int son) { 27 if( !son ) return; 28 for(int i=0;i<2;i++) 29 mx[fa][i] = max( mx[fa][i] , mx[son][i] ) , 30 mi[fa][i] = min( mi[fa][i] , mi[son][i] ); 31 } 32 inline void build(int pos,int dir,int l,int r) { 33 const int mid = ( l + r ) >> 1; 34 cmp = dir; 35 nth_element(ps+l,ps+mid,ps+r+1); 36 fill(pos,ps[mid]); 37 if( l < mid ) build(lson[pos]=++cnt,dir^1,l,mid-1); 38 if( mid < r ) build(rson[pos]=++cnt,dir^1,mid+1,r); 39 update(pos,lson[pos]) , update(pos,rson[pos]); 40 } 41 inline bool insqr(int p,int sx,int tx,int sy,int ty) { 42 return sx <= mi[p][0] && mx[p][0] <= tx 43 && sy <= mi[p][1] && mx[p][1] <= ty; 44 } 45 inline bool insqr(const Point &p,int sx,int tx,int sy,int ty) { 46 return sx <= p.d[0] && p.d[0] <= tx 47 && sy <= p.d[1] && p.d[1] <= ty; 48 } 49 inline bool outsqr(int p,int sx,int tx,int sy,int ty) { 50 return mx[p][0] < sx || tx < mi[p][0] 51 || mx[p][1] < sy || ty < mi[p][1]; 52 } 53 inline void update(int pos,int sx,int tx,int sy,int ty) { 54 if( !pos || outsqr(pos,sx,tx,sy,ty) ) return; 55 if( insqr(pos,sx,tx,sy,ty) ) { 56 ++lazy[pos]; 57 return; 58 } 59 if( insqr(nv[pos],sx,tx,sy,ty) ) ans[nv[pos].id]++; 60 update(lson[pos],sx,tx,sy,ty) , update(rson[pos],sx,tx,sy,ty); 61 } 62 inline void dfs(int pos) { 63 ans[nv[pos].id] += lazy[pos]; 64 if( lson[pos] ) lazy[lson[pos]] += lazy[pos] , dfs(lson[pos]); 65 if( rson[pos] ) lazy[rson[pos]] += lazy[pos] , dfs(rson[pos]); 66 } 67 68 int main() { 69 static int n,k,cn; 70 scanf("%d%d",&n,&k); 71 for(int i=1,x,y;i<=n;i++) { 72 scanf("%d%d%d",&x,&y,ind+i); 73 inx[i] = x + y , iny[i] = x - y; 74 ps[i] = (Point){ { inx[i] , iny[i] } , i }; 75 } 76 build(cnt=1,0,1,n); 77 for(int i=1;i<=n;i++) { 78 update(1, 79 max((lli)inx[i]-ind[i],-2147483648ll), 80 min((lli)inx[i]+ind[i],2147483647ll), 81 max((lli)iny[i]-ind[i],-2147483648ll), 82 min((lli)iny[i]+ind[i],2147483647ll)); 83 } 84 dfs(1); 85 for(int i=1;i<=n;i++) cn += ( ans[i] > k ); 86 printf("%d\n",cn); 87 for(int i=1;i<=n;i++) if( ans[i] > k ) printf("%d ",i); 88 puts(""); 89 return 0; 90 }
T3:

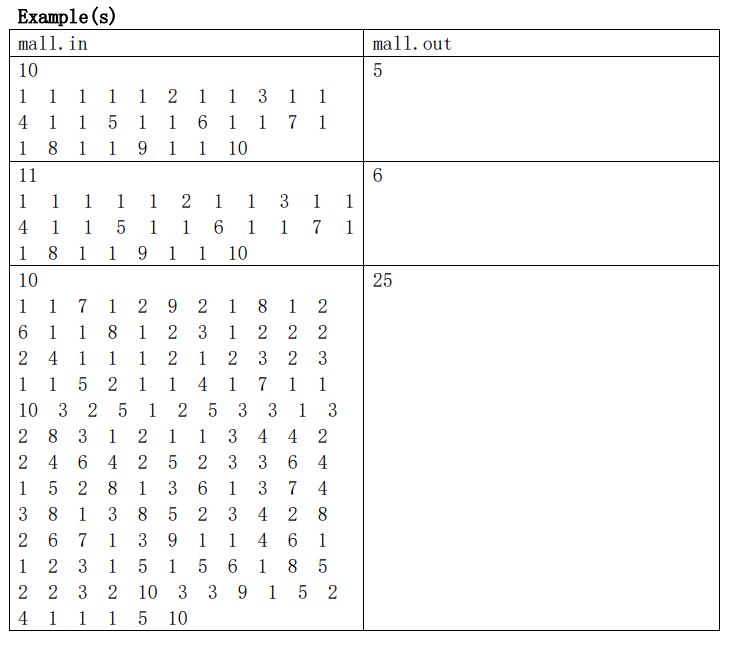
不能相互到达?不就是最大独立集?点数减最大匹配就好了。
等等,一般图最大匹配?这不是经典的NP问题吗?这题能做?
发现按照行列分组后这是一个二分图,然后就拿到了48分……
这个思路为什么有问题呢?因为一旦n为奇数的话,这图存在奇环,就不是二分图了……
根据鸽笼原理,一定有一行点数<=10,我们暴力枚举这一行状态,剩下的就是二分图了。
说着简单写着难系列。
考场48分代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<vector> 6 #include<queue> 7 #define debug cout 8 using namespace std; 9 const int maxn=2e2+1e1,maxm=maxn*maxn,maxe=55; 10 const int inf=0x3f3f3f3f; 11 12 int k[maxe],sum[maxn],n,full; 13 int st,ed; 14 15 struct Elevator { 16 int h,x,y; 17 friend bool operator < (const Elevator &a,const Elevator &b) { 18 if( a.h != b.h ) return a.h < b.h; 19 if( a.x != b.x ) return a.x < b.x; 20 return a.y < b.y; 21 } 22 friend bool operator == (const Elevator &a,const Elevator &b) { 23 return a.h == b.h && a.x == b.x && a.y == b.y; 24 } 25 }; 26 vector<Elevator> v; 27 28 namespace Flow { 29 int s[maxn],t[maxm<<1],nxt[maxm<<1],f[maxm<<1],dep[maxn]; 30 31 inline void coredge(int from,int to,int flow) { 32 static int cnt = 1; 33 t[++cnt] = to , f[cnt] = flow , 34 nxt[cnt] = s[from] , s[from] = cnt; 35 } 36 inline void singledge(int from,int to,int flow) { 37 coredge(from,to,flow) , coredge(to,from,0); 38 } 39 inline bool bfs() { 40 memset(dep,-1,sizeof(dep)) , dep[st] = 0; 41 queue<int> q; q.push(st); 42 while( q.size() ) { 43 const int pos = q.front(); q.pop(); 44 for(int at=s[pos];at;at=nxt[at]) { 45 if( f[at] && !~dep[t[at]] ) dep[t[at]] = dep[pos] + 1 , q.push(t[at]); 46 } 47 } 48 return ~dep[ed]; 49 } 50 inline int dfs(int pos,int flow) { 51 if( pos == ed ) return flow; 52 int ret = 0 , now = 0; 53 for(int at=s[pos];at;at=nxt[at]) 54 if( f[at] && dep[t[at]] > dep[pos] ) { 55 now = dfs(t[at],min(flow,f[at])); 56 ret += now , flow -= now , 57 f[at] -= now , f[at^1] += now; 58 if( !flow ) return ret; 59 } 60 if( !ret ) dep[pos] = -1; 61 return ret; 62 } 63 inline int dinic() { 64 int ret = 0 , now = 0; 65 while( bfs() ) { 66 while( ( now = dfs(st,inf) ) ) ret += now; 67 } 68 return ret; 69 } 70 } 71 72 inline int covdep(int dep,int pos) { 73 return sum[dep-1] + pos; 74 } 75 inline int cov(int id,int tpe) { // tpe == 0 means out point , 1 means in point 76 return id * 2 + tpe - 1; 77 } 78 79 inline void pre() { 80 sort(v.begin(),v.end()); 81 unsigned len = unique(v.begin(),v.end()) - v.begin(); 82 for(int i=1;i<=n;i++) sum[i] = sum[i-1] + k[i]; 83 full = sum[n] , st = full * 2 + 1 , ed = full * 2 + 2; 84 for(unsigned i=0;i<len;i++) { 85 const int x = covdep(v[i].h,v[i].x); 86 const int y = covdep(v[i].h!=n?v[i].h+1:1,v[i].y); 87 if( v[i].h & 1 ) { 88 Flow::singledge(cov(x,1),cov(y,0),1); 89 } else { 90 Flow::singledge(cov(y,1),cov(x,0),1); 91 } 92 } 93 for(int i=1;i<=full;i++) 94 Flow::singledge(cov(i,0),cov(i,1),1); 95 for(int i=1;i<=n;i++) 96 if( i & 1 ) { 97 for(int j=1;j<=k[i];j++) 98 Flow::singledge( st , cov(sum[i-1]+j,0) , 1 ); 99 } else { 100 for(int j=1;j<=k[i];j++) 101 Flow::singledge( cov(sum[i-1]+j,1) , ed , 1 ); 102 } 103 } 104 105 int main() { 106 static int h,x,y,ans; 107 scanf("%d",&n); 108 int t = 0; 109 while( scanf("%d%d%d",&x,&y,&h) == 3 ) { 110 v.push_back((Elevator){h,x,y}); 111 k[h] = max( k[h] , x ) , k[h!=n?h+1:1] = max( k[h!=n?h+1:1] , y ); 112 ++t; 113 } 114 pre(); 115 ans = full - Flow::dinic(); 116 printf("%d\n",ans); 117 return 0; 118 }
考后AC代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<vector> 6 #include<queue> 7 #define debug cout 8 using namespace std; 9 const int maxn=2e2+1e1,maxm=4e4+1e2,maxe=55; 10 const int inf=0x3f3f3f3f; 11 12 int k[maxe],sum[maxn],n,full,mip,ans; 13 int st,ed,len; 14 bool vis[maxn]; 15 16 struct Elevator { 17 int h,x,y; 18 friend bool operator < (const Elevator &a,const Elevator &b) { 19 if( a.h != b.h ) return a.h < b.h; 20 if( a.x != b.x ) return a.x < b.x; 21 return a.y < b.y; 22 } 23 friend bool operator == (const Elevator &a,const Elevator &b) { 24 return a.h == b.h && a.x == b.x && a.y == b.y; 25 } 26 }; 27 vector<Elevator> v; 28 29 namespace Flow { 30 int s[maxn],t[maxm<<1],nxt[maxm<<1],f[maxm<<1],dep[maxn],cnt=1; 31 32 inline void coredge(int from,int to,int flow) { 33 t[++cnt] = to , f[cnt] = flow , 34 nxt[cnt] = s[from] , s[from] = cnt; 35 } 36 inline void singledge(int from,int to,int flow) { 37 coredge(from,to,flow) , coredge(to,from,0); 38 } 39 inline bool bfs() { 40 memset(dep,-1,sizeof(dep)) , dep[st] = 0; 41 queue<int> q; q.push(st); 42 while( q.size() ) { 43 const int pos = q.front(); q.pop(); 44 for(int at=s[pos];at;at=nxt[at]) { 45 if( f[at] && !~dep[t[at]] ) dep[t[at]] = dep[pos] + 1 , q.push(t[at]); 46 } 47 } 48 return ~dep[ed]; 49 } 50 inline int dfs(int pos,int flow) { 51 if( pos == ed ) return flow; 52 int ret = 0 , now = 0; 53 for(int at=s[pos];at;at=nxt[at]) 54 if( f[at] && dep[t[at]] > dep[pos] ) { 55 now = dfs(t[at],min(flow,f[at])); 56 ret += now , flow -= now , 57 f[at] -= now , f[at^1] += now; 58 if( !flow ) return ret; 59 } 60 if( !ret ) dep[pos] = -1; 61 return ret; 62 } 63 inline int dinic() { 64 int ret = 0 , now = 0; 65 while( bfs() ) 66 while( ( now = dfs(st,inf) ) ) ret += now; 67 return ret; 68 } 69 inline void reset() { 70 memset(s,0,sizeof(s)) , cnt = 1; 71 } 72 } 73 74 inline int countbit(int x) { 75 #define lowbit(x) (x&-x) 76 int ret = 0; 77 while( x ) ++ret , x -= lowbit(x); 78 return ret; 79 } 80 inline int covdep(int dep,int pos) { 81 return sum[dep-1] + pos; 82 } 83 84 inline int rebuild(int sta) { 85 Flow::reset() , memset(vis,0,sizeof(vis)); 86 int ret = 0; 87 for(int i=0;i<k[mip];i++) if( ! ( sta & ( 1 << i ) ) ) vis[covdep(mip,i+1)] = 1; 88 for(int i=0;i<len;i++) { 89 const int h = v[i].h , th = h != n ? h + 1 : 1; 90 if( h == mip) { 91 if( ( 1 << ( v[i].x - 1 ) ) & sta ) vis[covdep(th,v[i].y)] = 1; 92 } 93 else if( th == mip ) { 94 if( ( 1 << ( v[i].y - 1 ) ) & sta ) vis[covdep(h,v[i].x)] = 1; 95 }else { 96 if( ( h > mip && ( ( h - mip ) & 1 ) ) || ( h < mip && ! ( ( mip - h ) & 1 ) ) ) 97 Flow::singledge(covdep(h,v[i].x),covdep(th,v[i].y),1); 98 else Flow::singledge(covdep(th,v[i].y),covdep(h,v[i].x),1); 99 } 100 } 101 for(int i=1;i<=n;i++) { 102 if( ( i > mip && ( ( i - mip ) & 1 ) ) || ( i < mip && !( ( mip - i ) & 1 ) ) ) { 103 for(int j=1;j<=k[i];j++) 104 if( !vis[covdep(i,j)] ) Flow::singledge(st,covdep(i,j),1); 105 } else if( i != mip ) { 106 for(int j=1;j<=k[i];j++) 107 if( !vis[covdep(i,j)] ) Flow::singledge(covdep(i,j),ed,1); 108 } 109 } 110 for(int i=1;i<=full;i++) ret += !vis[i]; 111 ret -= Flow::dinic(); 112 return ret; 113 } 114 inline void getansodd() { 115 int fs = ( 1 << k[mip] ); 116 for(int i=0;i<fs;i++) ans = max( ans , rebuild(i) ); 117 } 118 inline void getanseven() { 119 for(int i=0;i<len;i++) { 120 const int x = covdep(v[i].h,v[i].x); 121 const int y = covdep(v[i].h!=n?v[i].h+1:1,v[i].y); 122 if( v[i].h & 1 ) Flow::singledge(x,y,1); 123 else Flow::singledge(y,x,1); 124 } 125 for(int i=1;i<=n;i++) { 126 if( i & 1 ) { 127 for(int j=1;j<=k[i];j++) 128 Flow::singledge( st , covdep(i,j) , 1 ); 129 } else { 130 for(int j=1;j<=k[i];j++) 131 Flow::singledge( covdep(i,j) , ed , 1 ); 132 } 133 } 134 ans = full - Flow::dinic(); 135 } 136 137 inline void pre() { 138 sort(v.begin(),v.end()); 139 len = unique(v.begin(),v.end()) - v.begin(); 140 for(int i=1;i<=n;i++) sum[i] = sum[i-1] + k[i]; 141 full = sum[n] , st = full + 1 , ed = full + 2; 142 *k = inf; 143 for(int i=1;i<=n;i++) if( k[i] < k[mip] ) mip = i; 144 } 145 146 int main() { 147 static int h,x,y; 148 scanf("%d",&n); 149 int t = 0; 150 while( scanf("%d%d%d",&x,&y,&h) == 3 ) { 151 v.push_back((Elevator){h,x,y}); 152 k[h] = max( k[h] , x ) , k[h!=n?h+1:1] = max( k[h!=n?h+1:1] , y ); 153 ++t; 154 } 155 pre(); 156 if( n & 1 ) getansodd(); 157 else getanseven(); 158 printf("%d\n",ans); 159 return 0; 160 }
话说在从老家回来汽车上写这东西真是晃死我了……



 浙公网安备 33010602011771号
浙公网安备 33010602011771号