『模拟赛题解』10.3 NOIP 模拟赛
10.3 NOIP 模拟赛
T1. 不稳定的道路
Description
有 \(n\) 个城市和 \(m\) 条道路。城市编号 \(1\) 至 \(n\) ,道路编号 \(1\) 到 \(m\) 。道路 \(i\) 双向连接城市 \(a_i\) 和城市 \(b_i\) 。
但是通过每一条道路,所需的时间却是不稳定的,跟出发的时刻有关,如果在时刻 \(t\) 通过道路 \(i\) ,那么需要的时间为:\(c_i + \lfloor \! \frac{d_i}{t + 1} \! \rfloor\) 。其中 \(c_i\) 和 \(d_i\) 是给出的整数,并且上面这个式子的计算需要向下取整。
你计划从城市 \(1\) 去往城市 \(n\) ,这个过程中你可以在任何城市进行停留(不必立即出发)。问最早到达城市 \(n\) 的时间。如果无法到达城市 \(n\),请输出 \(-1\) 。
Solution
题目中边权的计算公式是 \(c_i + \lfloor \! \frac{d_i}{t + 1} \! \rfloor\),其中 \(c_i\) 不会改变。对于后面的部分,不难发现当 \(t > \sqrt{d_i} + 1\) 时,直接走显然最优,否则就等到 \(\sqrt{d_i} + 1\)。所以直接对于每种情况的 \(t\) 建边,跑最短路就行。
Code
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int maxn = 1e5 + 10;
int n, m, cnt;
int head[maxn];
struct Edge
{
int to, nxt, c, d, g;
} edge[maxn * 2];
priority_queue < pair <int, int> > q;
int dis[maxn];
bool vis[maxn];
void addedge(int x, int y, int c, int d, int g)
{
edge[++ cnt] = (Edge){y, head[x], c, d, g};
head[x] = cnt;
}
signed main()
{
freopen("road.in", "r", stdin);
freopen("road.out", "w", stdout);
cin >> n >> m;
for (int i = 1; i <= m; i ++)
{
int x, y, c, d;
cin >> x >> y >> c >> d;
int g = (int)sqrt(d);
if (d - g * g > (g + 1) * (g + 1) - d)
g ++;
g --;
addedge(x, y, c, d, g);
addedge(y, x, c, d, g);
}
for (int i = 1; i <= n; i ++)
dis[i] = 1e18;
dis[1] = 0;
q.push(make_pair(0, 1));
while (!q.empty())
{
int t = -q.top().first;
int x = q.top().second;
q.pop();
if (vis[x])
continue;
vis[x] = 1;
for (int i = head[x]; i; i = edge[i].nxt)
{
int y = edge[i].to, g = edge[i].g;
if (vis[y])
continue;
if (t <= g)
{
if (dis[y] > g + edge[i].c + edge[i].d / (g + 1))
{
dis[y] = g + edge[i].c + edge[i].d / (g + 1);
q.push(make_pair(-dis[y], y));
}
}
else
{
if (dis[y] > t + edge[i].c + edge[i].d / (t + 1))
{
dis[y] = t + edge[i].c + edge[i].d / (t + 1);
q.push(make_pair(-dis[y], y));
}
}
}
}
if (dis[n] == 1e18)
cout << -1;
else
cout << dis[n];
return 0;
}
T2. 小 A 的数
Description
给出一棵 \(n\) 个点的树,每个点有黑白两种颜色。
\(q\) 次询问,每次询问给出 \(x\) 和 \(y\) ,问能否选出一个 \(x\) 个点的联通子图,使得其中黑点数目为 \(y\) 。
Solution
发现 \(n \le 5000\),所以直接预处理显然不行。
所以考虑树形 dp,显然对于某一大小的连通子图,其包含黑点数的最小值与最大值之间的所有点数目都能够取得到(一个连通子图删除一个点再加入一个点后,黑点的数目变化最多只为 \(1\) 。因此可以变化到\([\min, \,\max]\) 之间所有的数目)。
考虑树形背包,设 \(f_{i, j}\) 表示从 \(i\) 的子树中选出大小为 \(j\) 的连通子图黑点的最小值;\(g_{i, j}\) 表示最大值。用树形背包转移。
注意只能使用已经遍历过的点数目和当前子树中的点数目转移,否则在遇到链时会退化成 \(O(n^3)\)。
Code
#include <bits/stdc++.h>
using namespace std;
const int maxn = 5e3 + 5;
int n, q, cnt;
int head[maxn], col[maxn], sz[maxn], f[maxn][maxn], g[maxn][maxn];
struct Edge
{
int nxt, to;
} edge[maxn << 1];
void addedge(int x, int y)
{
edge[++ cnt].to = y;
edge[cnt].nxt = head[x];
head[x] = cnt;
}
void dfs(int x, int fa)
{
sz[x] = 1;
f[x][1] = g[x][1] = col[x];
for (int i = head[x]; i; i = edge[i].nxt)
{
int y = edge[i].to;
if (y == fa)
continue;
dfs(y, x);
for (int j = sz[x]; j; j --)
for (int k = sz[y]; k; k --)
{
f[x][j + k] = min(f[x][j + k], f[x][j] + f[y][k]);
g[x][j + k] = max(g[x][j + k], g[x][j] + g[y][k]);
}
sz[x] += sz[y];
}
for (int i = 1; i <= n; i ++)
{
f[0][i] = min(f[0][i], f[x][i]);
g[0][i] = max(g[0][i], g[x][i]);
}
}
int main()
{
freopen("tree.in", "r", stdin);
freopen("tree.out", "w", stdout);
int t;
cin >> t;
cin >> n >> q;
for (int i = 1; i < n; i ++)
{
int x, y;
cin >> x >> y;
addedge(x, y);
addedge(y, x);
}
for (int i = 1; i <= n; i ++)
cin >> col[i];
memset(f, 0x3f, sizeof f);
dfs(1, 0);
while (q --)
{
int x, y;
cin >> x >> y;
if (y >= f[0][x] && y <= g[0][x])
cout << "YES\n";
else
cout << "NO\n";
}
return 0;
}
T3. 吵架
Description
老虎和蒜头是好朋友,但他们经常吵架。吵完架之后,两人会各自去到一个僻静的角落,使得它们的距离最远。
他们所在的小镇有 \(n\) 个角落,有 \(n - 1\) 条长度为 \(1\) 的道路每条连接两个角落,角落互相可达;两个角落的距离等于它们之间简单路径的长度;起初所有的角落都是僻静的。
从 \(1\) 到 \(q\) 这 \(q\) 天,每天会发生一个事件,用以下两者之一描述:
- \(C \; x\) :角落 \(x\) 的僻静性发生反转(原来僻静则现在吵闹,原来吵闹则现在僻静)
- \(G\) :老虎和蒜头吵了一次架,你需要输出当它们各自去到想去的僻静角落之后它们之间的距离。这对角 落应是所有僻静角落对中相距最远的一对。特别地,如果只有一个僻静的角落,输出 \(0\) ;如果所有角落都吵闹,输出 \(-1\)。
Solution
\(n\) 个点,\(n - 1\) 条边的连通图,这显然是一棵树。
则操作 2 就变成了求树的直径(两个端点都是僻静的角落)。但是看到数据范围,只能用 \(O(n \log n)\) 的东西去维护直径了,恰好昨天又练了一下午加一晚上的线段树,很容易想到了用线段树来维护直径。
怎么维护呢?线段树的每个区间 \([l, \,r]\) 表示点集 \([l, \,r]\) 的直径。吵闹的点设成 \([-1, \,-1]\),僻静的点设成 \([x, \,x]\)。
Code
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 5;
int n, q, cnt;
int dep[maxn], head[maxn];
int f[maxn][20];
int flag[maxn];
int lg2[maxn];
bool vis[maxn];
struct Edge
{
int to, nxt;
} edge[maxn];
struct node
{
int l, r, a = -1, b = -1;
} tree[maxn * 4];
void addedge(int x, int y)
{
edge[++ cnt].to = y;
edge[cnt].nxt = head[x];
head[x] = cnt;
}
void dfs(int x, int fa)
{
if (vis[x])
return ;
vis[x] = true;
dep[x] = dep[fa] + 1;
f[x][0] = fa;
for (int i = 1; i <= lg2[dep[x]]; i ++)
f[x][i] = f[f[x][i - 1]][i - 1];
for (int i = head[x]; i; i = edge[i].nxt)
dfs(edge[i].to, x);
}
int lca(int x, int y)
{
if (dep[x] < dep[y])
swap(x, y);
while (dep[x] != dep[y])
x = f[x][lg2[dep[x] - dep[y]]];
if (x == y)
return x;
for (int k = lg2[dep[x]]; k >= 0; k --)
if (f[x][k] != f[y][k])
{
x = f[x][k];
y = f[y][k];
}
return f[x][0];
}
int dis(int x, int y)
{
if (x == -1 || y == -1)
return -0x3f3f3f3f + x + y;
return dep[x] + dep[y] - 2 * dep[lca(x, y)];
}
void pushup(int q)
{
tree[q].a = tree[q].b = -1;
int p[4] = {tree[q << 1].a, tree[q << 1].b, tree[q << 1 | 1].a, tree[q << 1 | 1].b};
for(int i = 0;i < 4;++ i)
for(int j = 0;j < i;++ j){
int x = p[i], y = p[j];
if(dis(x, y) > dis(tree[q].a, tree[q].b))
tree[q].a = x, tree[q].b = y;
}
}
void build(int q, int l, int r)
{
tree[q].l = l;
tree[q].r = r;
if(l == r)
{
tree[q].a = tree[q].b = l;
return;
}
int mid = l + r >> 1;
build(q << 1, l, mid);
build(q << 1 | 1, mid + 1, r);
pushup(q);
}
void modify(int q, int l, int r, int k)
{
if (tree[q].l >= l && tree[q].r <= r)
{
tree[q].a = tree[q].b = k;
return ;
}
int mid = tree[q].l + tree[q].r >> 1;
if (mid >= l)
modify(q << 1, l, r, k);
if (mid < r)
modify(q << 1 | 1, l, r, k);
pushup(q);
}
int main()
{
freopen("quarrel.in", "r", stdin);
freopen("quarrel.out", "w", stdout);
cin >> n >> q;
for(int i = 1;i < n; i ++)
{
int a, b;
cin >> a >> b;
addedge(a, b);
addedge(b, a);
}
for (int i = 2; i <= n; i ++)
lg2[i] = lg2[i / 2] + 1;
dfs(1, 0);
build(1, 1, n);
int num = n, x;
for (int i = 1;i <= q; i ++)
{
char op;
cin >> op;
if(op == 'G')
{
if (num == 1)
cout << "0\n";
else if (num == 0)
cout << "-1\n";
else
cout << dis(tree[1].a, tree[1].b) << endl;
}
else
{
cin >> x;
flag[x] ^= 1;
if (flag[x] == 1)
num --, modify(1, x, x, -1);
else
num ++, modify(1, x, x, x);
}
}
return 0;
}
T4. 选数问题 V2
Description
给一个长度为 \(n\) 的数组 \(a\) ,数据保证每个 \(a_i\) 的约数数量不超过 \(7\) ,求最少选出多少个数(同一个数不能选 \(2\) 次),使得选出的数乘积为完全平方数。无解输出 \(-1\) 。
Solution
由于每个数的约数数量小于等于 \(7\) ,因此可知每个数的不同质因子数量小于 \(3\) ,否则约数数量至少是 \(8\) 。也就是说这些数的质因子数量最多只有 \(2\) 个。
同时对于每个数,去掉其中的平方因子,例如:\(8\) 变为 \(2\) ,不会影响最终的结果。
对于去除平方因子后的数,我们分类讨论:
- 存在数字 \(1\) ,则直接返回 \(1\) 。
- 对于质数(只有 \(1\) 个质因子的数),如果成对出现,则返回 \(2\) 。
- 对于有 \(2\) 个质因子的数,我们以质因子作为点(包括 \(1\) ),数字作为边建图(质数则是 \(1\) 到 \(p\) 的边),然后在图中找出一个最小的环就是答案。
由于小于 \(10^6\) 的质数数量,接近 \(8 \times 10^4\) 个,因此如果用 floyd 求解是 \(O(n^3)\) 的,考虑优化。
由于 \(a_i \le 10^6\) ,因此 \(a_i\) 不存在两个都大于 \(10^3\) 的质因子,因此如果存在环,那么环一定经过小于 \(10^3\) 的点。因此我们将找全局最小环的问题转为找以小于 \(10^3\) 的质因子为起点的最小环。
在固定起点的情况下,我们可以直接用 BFS 来处理(因为权值为 \(1\) )。BFS 的过程中记录节点的深度 \(d_i\) ,如果发现某个节点已经被访问过,则一定存在环,环的长度可以简单记为 \(d_i + d_j + 1\) ,其中 \(i, j\) 是当前访问的边的两个端点,这样单次处理的时间复杂度为 \(O(n)\) 。
我们考虑,有时直接用 \(d_i + d_j + 1\) 来计算最小环的长度,是不正确的,例如:
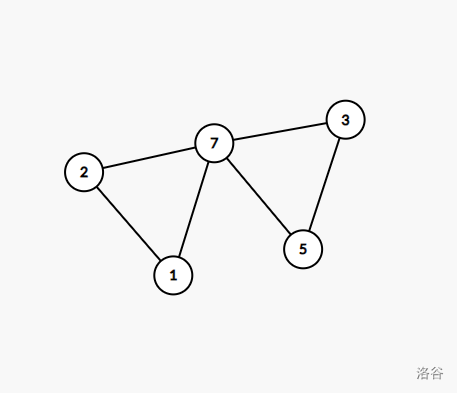
从 \(5\) 开始做 BFS,到 \(1\) 的距离是 \(3, 2\) ,按照 \(d_i + d_j + 1\) 计算环长是 \(6\) ,不过我们是枚举所有点为起点进行计算的,当我们枚举点 \(7\) 时,就可以得到那个最小环的长度了。
一个小小的优化是,当我们当前的 BFS 不能得到小于当前最优的答案时就可以退出了,因为后面不会 得到更优的结果了。时间复杂度为 \(O(\dfrac{n\sqrt n}{\log n})\)。
Code
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 1;
int n, cnt, x, s, ans = 0x3f3f3f3f;
bool flag;
int a[maxn], q[maxn], d[maxn], p[maxn];
vector <int> g[maxn];
int main()
{
freopen("choose.in", "r", stdin);
freopen("choose.out", "w", stdout);
cin >> n;
for (int i = 1; i <= n; i ++)
cin >> a[i];
for (int i = 1; i <= n; i ++)
{
cnt = 0;
q[2] = 1;
for (int j = 2; j * j <= a[i]; j ++)
{
x = 0;
while (a[i] % j == 0)
{
a[i] /= j;
x ++;
}
if (x & 1)
q[++ cnt] = j;
}
if (a[i] > 1)
q[++ cnt] = a[i];
if (cnt == 0)
ans = 1;
g[q[1]].push_back(q[2]);
g[q[2]].push_back(q[1]);
}
for (int i = 1; i <= 1000; i ++)
{
for (int j = 1; j < maxn; j ++)
d[j] = 0x3f3f3f3f;
d[i] = 0;
s = cnt = 0;
q[++ cnt] = i;
while (s < cnt)
{
x = q[++ s];
for (int j = 0; j < g[x].size(); j ++)
{
if (g[x][j] != p[x])
{
if (d[g[x][j]] == 0x3f3f3f3f)
{
d[g[x][j]] = d[x] + 1;
p[g[x][j]] = x;
q[++ cnt] = g[x][j];
}
else
ans = min(ans, d[x] + d[g[x][j]] + 1);
}
}
}
}
if (ans == 0x3f3f3f3f)
cout << -1;
else
cout << ans;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号