Matlab程序学习(散点边界线/包络线)

针对散点边界线，Matlab重的convhull为凸包络线，往往不能满足实际工作需要。

作散点的紧致包络线，需要考虑到凹凸点，为减少包络线与散点数据的过度紧密(穿过全散点)，并不过度包络(类似convhull)，从以下思路来实现：

1.散点数据按行走方向排序，并判断点的凹凸；

2.针对凹点，添加阈值，通过夹角判断，去除部分凹点，然后继续此种循环判断，直到所有凹点满足要求；

程序文件:

function y2=ScatterHull(Data,ang_2)
% Thinking from Dsp Tian 
% http://www.cnblogs.com/tiandsp/p/4006575.html
% y1(:,1)=x;y1(:,2)=y;ang_2:concave min angle
% ang_2=180:conhull;ang_2=0:all scatters
y1=unique(Data,'rows');% Remove duplicate rows 
%%
% sort of scatters
    cen=mean(y1);
    ang=atan2(y1(:,1)-cen(1),y1(:,2)-cen(2)); %每个点到坐标中心极角
    y1=[y1,ang];
    y1=sortrows(y1,3);    %按极角排序
    y1=y1(:,1:2);
%%
y2=y1;
im=1;
[n m]=size(y1);
%%
while length(im)>0
 
im=[];
%向量计算，判断凹点
for i=1:n    
    if i==1  %处理第一个点
        v1=y1(n,:)-y1(1,:);
        v2=y1(2,:)-y1(1,:); 
    elseif i==n %最后一个点
        v1=y1(n-1,:)-y1(n,:);    
        v2=y1(1,:)-y1(n,:);        
    else 
        v1=y1(i-1,:)-y1(i,:);     
        v2=y1(i+1,:)-y1(i,:);
    end
    r=det([v1;v2]);  %叉乘后向量方向
    c=dot(v1,v2)/(norm(v1)*norm(v2));
    ang=rad2deg(acos(c));
        
    if r<=0&(ang<ang_2|isnan(ang)==1)%concave
            ang(ang<ang_2)=[];
            im=[im;i];
    end
end
y2(im,:)=[];
y1=y2;
[n m]=size(y1);
end
%%
y2=[y2;y2(1,:)];%result's curve is closed
end

 

 

主程序:

function samplef
%UNTITLED5 Summary of this function goes here
%   Detailed explanation goes here
close all
clear all
clc
t=load('data2.txt');
t(t(:,1)==0|t(:,2)==0,:)=[];
x=t(:,1);
y=t(:,2);
figure(1)
ang=[0 60 120 180];
for i=1:4
t2=ScatterHull(t,ang(i));
t2=[t2;t2(1,:)];%画图使封闭
subplot(2,2,i)
hold on
plot(t(:,1),t(:,2),'ro')
plot(t2(:,1),t2(:,2),'g-')
legend('scatter','HullCurve','Location','NorthWest')
title(num2str(ang(i)))
end
end

 

结果：

 

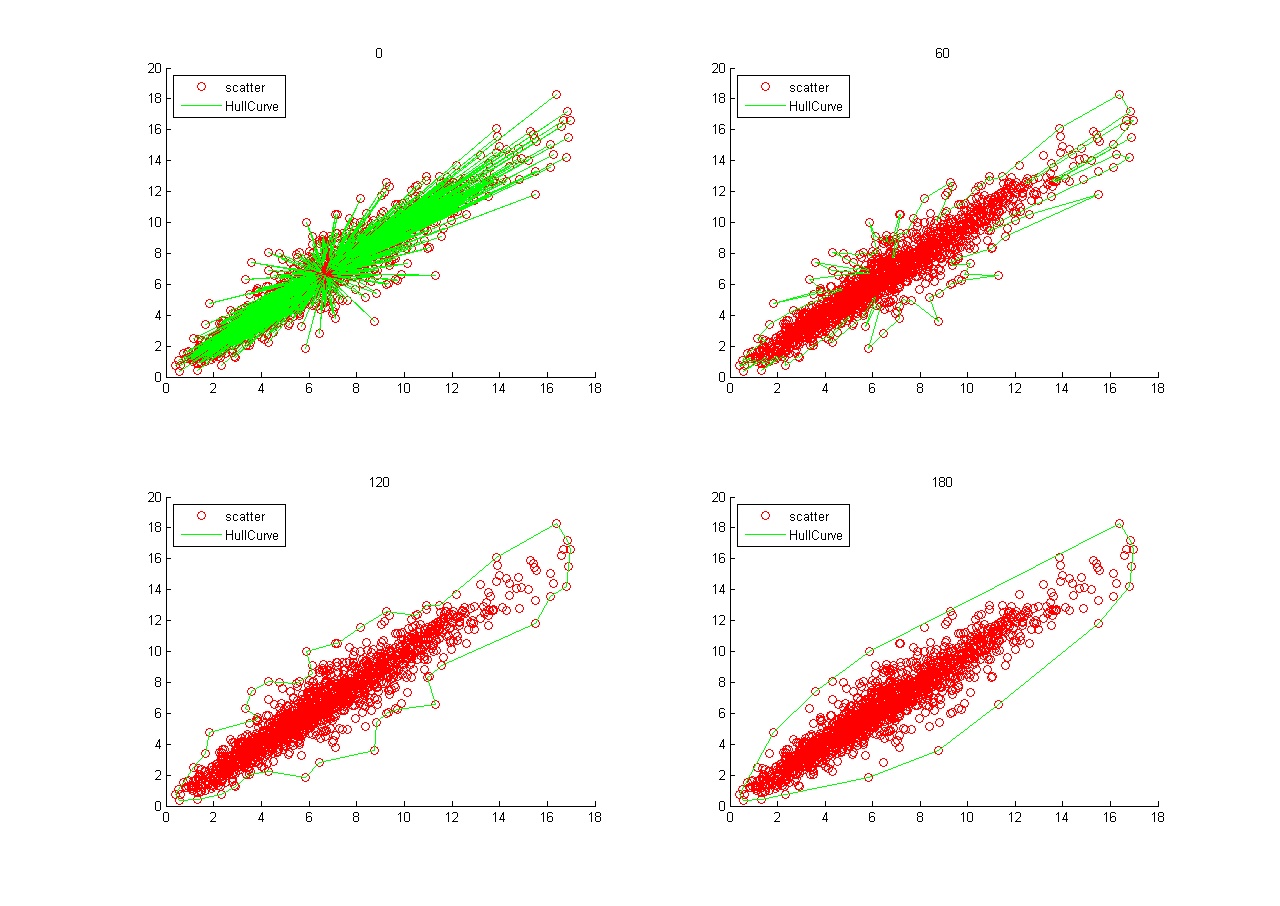
注意:部分散点极度不规则的情况，效果并不理想，例如散点图明显分区，具有几个明显的聚点中心