Learn Dijkstra For The Last Time
博客链接:https://www.codein.icu/learn-dijkstra/
Introduction
Dijkstra 算法是用于求解非负权图单源最短路的经典算法。
市面上的大部分教程都仅仅停留在「如何实现 Dijkstra 算法」的层面。从应用角度,这当然无可厚非。但理解算法本身,也不失为一件乐事。
问自己这样几个问题:
- Dijkstra 算法的每个过程是在干什么?
- Dijkstra 算法为什么是正确的?
也许你在小学就已经能熟练的打出 Dijkstra 的板子,拿它在各大 OJ 上厮杀。
也许你曾经随便找一篇博文,花费 10min 把代码敲熟便「学会了」Dijkstra 算法。
That is not true.
在我给小 OIer 们准备上最短路课程时,我才真正意识到,其实我从未理解过 Dijkstra 算法。我可以手指不停地将它敲出来,也会记录最短路径、最短路计数之类的拓展,但我不明白它的 Key Inspiration 是什么,不理解它「为什么」这么做,「为什么」是正确的。
我振臂高呼——「Tell Me Why!!!」
于是我花费了许多时间,在网上查找相关资料,但要么只能查到诘屈聱牙的严谨理论证明,要么就是 csdn 之流的垃圾场上千篇一律的不求甚解。
最后,我在 Stack Overflow 上找到了一篇回答,用一个形象的比喻解决了我的困惑。以此为立足点,刷新了我对 Dijkstra 的理解。也许这算是一种「Aha! moment」.
这便是本文的由来。
Analogy
Start With BFS
我们曾经学过 BFS(Breath-First Search,宽度优先搜索),如果没有学过的话建议先学习一下。
BFS 同样可以求解最短路,不过它有着更强的限制条件——「边的距离相等」,或者说,「边权为 \(1\)」.
在 BFS 的过程中,每个节点「首次」被访问,即为最短路。
这个是很好理解的,因为我们第一轮 BFS 访问的节点距离起点距离为 \(1\),第二轮距离为 \(2\),以此类推,首次访问某节点,就一定通过了最短的路径。
用一个形象的比喻:每一条边就像是一根 \(1m\) 长的管道,从起点开始注水,水流速度为 \(1m/s\),每个结点首次被水浸泡时,对应的是时间 \(t\) 最小,而 \(s = vt\),那么路程也最小,即最短路。
Water Filling
再回到我们的 Dijkstra 算法上。
相比于 BFS 的图,我们现在的图有何不同呢?
- 边权可以 \(>1\)
- 边权可以为 \(0\)
第二条暂且不谈,因为 BFS 事实上是可以处理边权为 0/1 的图的,只需要使用双端队列,将边权为 0 的边拓展的点插入队头即可。这个叫做 0-1 BFS.
我们可以沿用 BFS 的思路求最短路。可以将这张图转化为 BFS 能处理的图。
拆边建虚点。
比如说,有一条边权为 \(2\) 的边,我们把它拆成两条边权为 \(1\) 的边,以此类推,不就能将图转化为 BFS 可处理的图了吗?
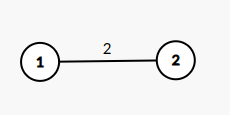
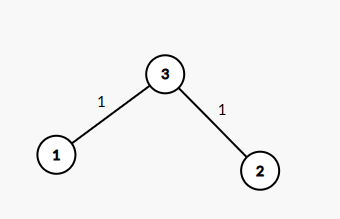
这样一来,我们就得到了一个复杂度为 \(O(\sum w)\) 的算法。由于边权可以很大,这个算法的复杂度是不可接受的。
可以怎么样优化一下呢?其实,每次只走 \(1m\) 是非常无效的行为。可以想想办法,让我们能一次走更长的距离。
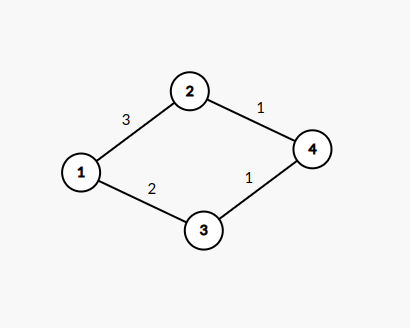
比如在这张图上,从 1 号结点出发,我们开始拓展:
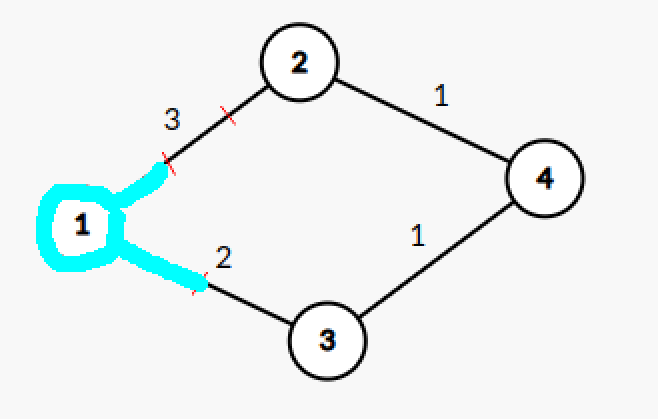
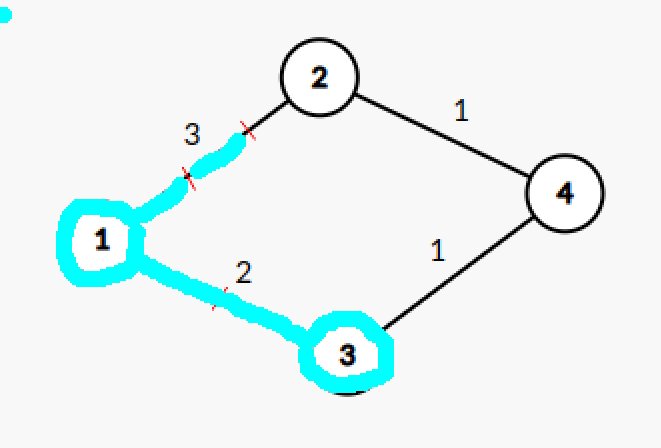
我们真正关注的,事实上是「实际存在的点」,而中间的步骤是无关紧要的。
比如上面这个过程,经过了两步,才抵达了 3 号结点。那能不能找到一种方法,一次性走过很多步而直接抵达 3 号结点呢?
其实是可以的。
Solution
我们将所有的、已经被水浸泡的点的集合,记做集合 \(\mathbf{S}\).
根据我们先前的描述,可以知道,集合 \(\mathbf{S}\) 中的点,都已经求出了最短路距离 \(dis\).
水将从集合 \(\mathbf{S}\) 中的点,经过管道继续流向其他点。下一个被浸泡的点,一定是已被浸泡的点的相邻点。
我们将与集合 \(\mathbf{S}\) 点相邻的所有点的集合记为集合 \(\mathbf{T}\).
- 集合 \(\mathbf{T}\) 中的点未被浸泡。
- 每个点首次被浸泡时,水流一定走的是最短路。对应的距离即为最短路距离。
- 下一个被浸泡的点一定从集合 \(\mathbf{T}\) 中产生。
现在,我们要做的就是,在集合 \(\mathbf{T}\) 中找到下一个被浸泡的点。
我们将某个点加入集合 \(\mathbf{S}\) 后,会更新起点到其相邻点的距离 \(dis\).
下一个被浸泡的点,一定是集合 \(\mathbf{T}\) 中 \(dis\) 最小,也就是离起点最近的点。
这样,算法流程就明确了:
- 初始,将起点加入集合 \(\mathbf{S}\),将相邻点加入集合 \(\mathbf{T}\)
- 找出集合 \(\mathbf{T}\) 中距离起点最近的点,加入集合 \(\mathbf{S}\),将其相邻点加入集合 \(\mathbf{T}\)
- 重复第二步,直到所有点都加入集合 \(\mathbf{S}\)
这就像是做了一个加速:我们的水本来要经过许多步才能泡到下一个节点,但我们跳过中间步骤,直接泡到下一个节点。
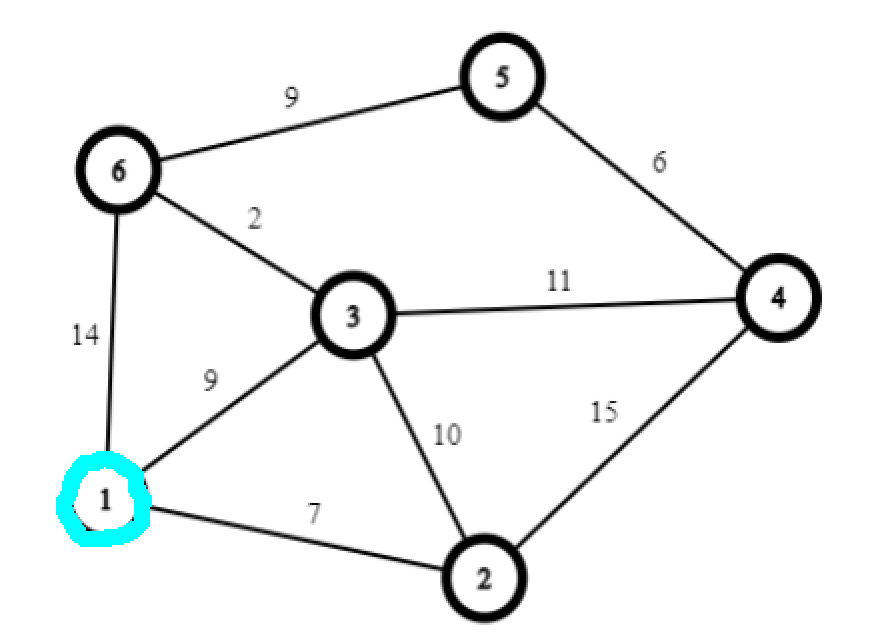
从 1 号点出发,发现浸泡到下一个节点需要走 7 步。
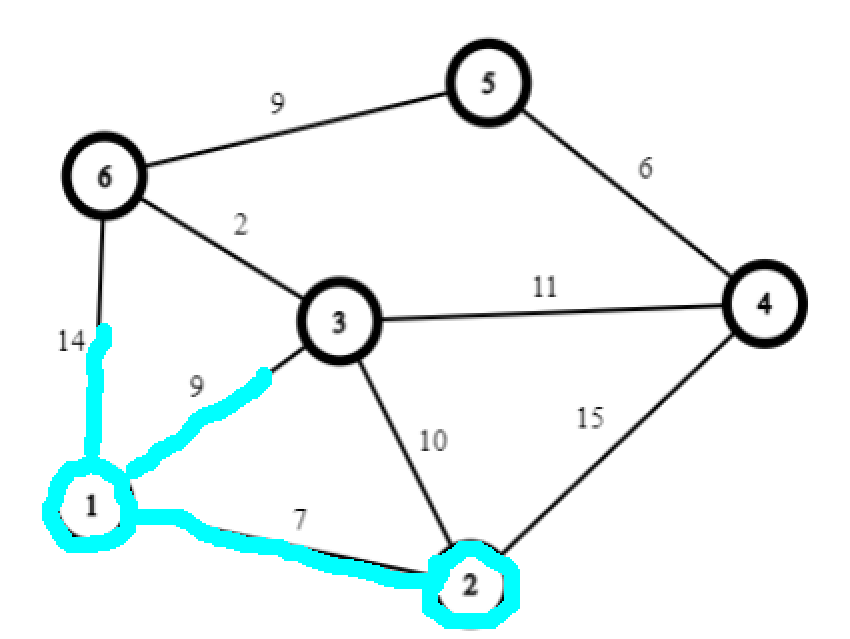
合七步为一步,接下来发现浸泡三号节点是最快的。
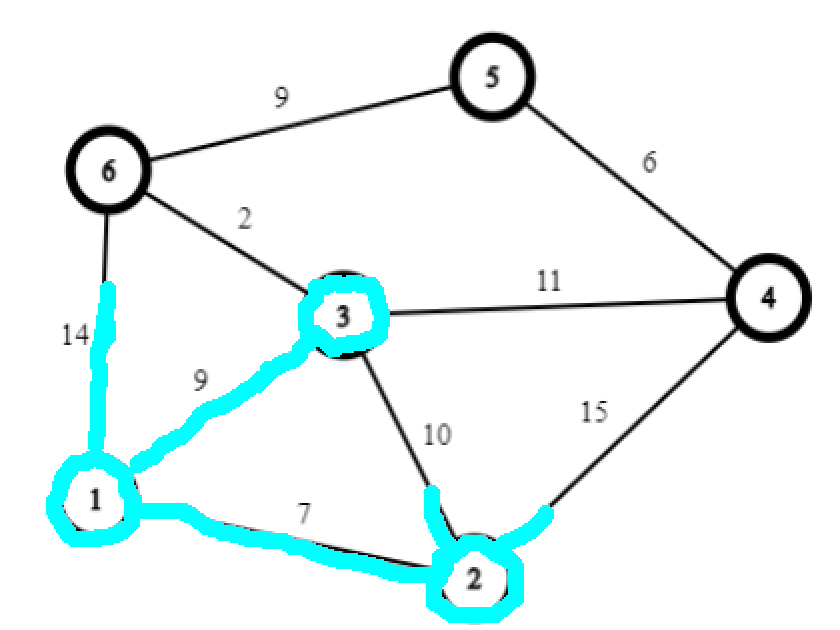
接下来,从 3 号出发浸泡 6 号节点是最快的。
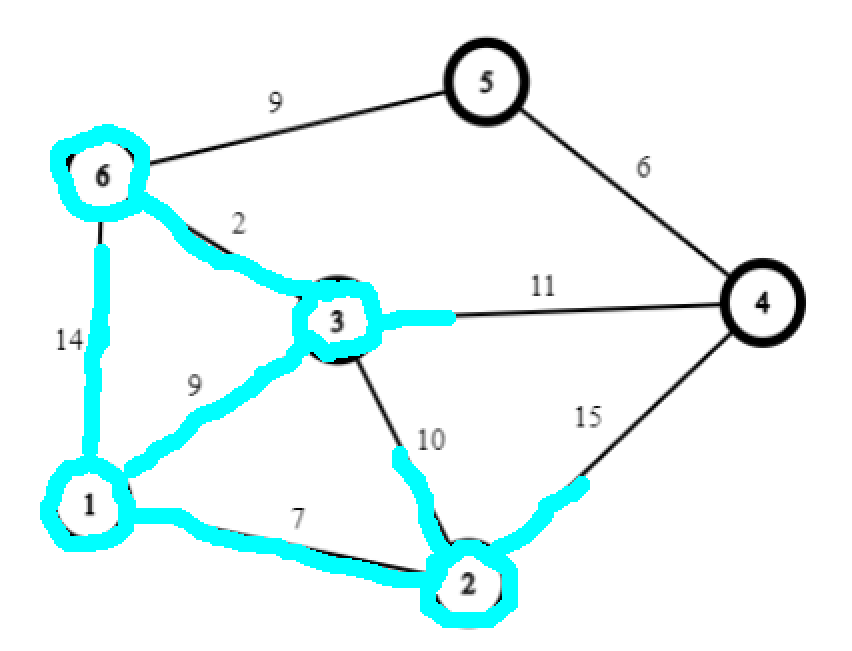
以此类推……剩下的就不画了。
Proof
从形象到抽象。
- 初始,将起点加入集合 \(\mathbf{S}\),将相邻点加入集合 \(\mathbf{T}\)
- 找出集合 \(\mathbf{T}\) 中距离起点最近的点,加入集合 \(\mathbf{S}\),将其相邻点加入集合 \(\mathbf{T}\)
- 重复第二步,直到所有点都加入集合 \(\mathbf{S}\)
定义当前情况下从起点到点 \(u\) 的最短距离为 \(\operatorname{D}(u)\),从起点到点 \(u\) 的真实最短距离为 \(\operatorname{dis}(u)\). 显然有:\(\operatorname{D}(u) \ge \operatorname{dis}(u)\).
第二步中,找出集合 \(\mathbf{T}\) 中 \(\operatorname{D}(u)\) 最小的点 \(u\),证明该点满足 \(\operatorname{D}(u) = \operatorname{dis}(u)\).
根据定义,集合 \(\mathbf{T}\) 中的点与集合 \(\mathbf{S}\) 中的点直接相连,而 \(\operatorname{D}(u) = \operatorname{dis}(x) + w\),目前的最短路就是从 \(x\) 点经过某条边到达 \(u\) 点。
当前的 \(\operatorname{D}(u)\) 是所有从集合 \(\mathbf{S}\) 中点出发,经过一条边到达 \(u\) 点的路径的最小距离。
从起点到达 \(u\) 点的最短路径的一部分一定也是最短路径。
比如途中经过某点 \(x\),则当前路径一定也是起点到达 \(x\) 的最短路径。
否则,走起点到达 \(x\) 的最短路径,再走剩下的路径,即可得到起点到达 \(u\) 点的一条更短路,矛盾。
假设存在某一条更短路能取得 \(\operatorname{dis}(u) < \operatorname{D}(u)\),那么这条更短路,一定是从集合 \(\mathbf{S}\) 中某点出发,经过至少两条边后到达 \(u\) 点。
证明:若只经过一条边,则该更短路本来会更新 \(\operatorname{D}(u)\),使得 \(\operatorname{D}(u) = \operatorname{dis}(u)\),矛盾。
现在证明,该更短路不存在。
我们当前的最短路可以记做:\(x \to u\).
而更短路可以记做:\(y \to t \to \ldots \to u\),其中 \(\ldots\) 是任意路径,可以包含 \(0\) 及更多个点。
\(x,y \in \mathbf{S}\),那么 \(u,y \in \mathbf{T}\).
根据定义,\(\operatorname{D}(u)\) 是集合 \(\mathbf{T}\) 中最小的,那么 \(\operatorname{D}(u) \le \operatorname{D}(t)\).
那么从 \(t\) 点出发,再经过某条路径到达 \(u\) 点,记该路径长度为 \(L\),只要满足 \(L \ge 0\),就有 \(\operatorname{D}(t) + L \ge \operatorname{D}(u)\).
那么这条路径一定不能取得比当前 \(\operatorname{D}(u)\) 更优的值。
因此,该更短路不存在。
PS:这里还能看出 Dijkstra 为什么不能处理负权图。在负权图上,\(L < 0\) 会导致 \(\operatorname{D}(t) + L \ge \operatorname{D}(u)\) 这个不等式并不成立,核心的贪心思想就无效了。
此时,取出 \(\operatorname{D}(u)\) 最小的点,也未必满足 \(\operatorname{D}(u) = \operatorname{dis}(u)\).
接下来,每次第二步加入集合 \(\mathbf{S}\) 的点都满足 \(\operatorname{D}(u) = \operatorname{dis}(u)\),而初始起点显然也满足,则集合 \(\mathbf{S}\) 中的点都满足 \(\operatorname{D}(u) = \operatorname{dis}(u)\).
Implementation
描述到这里,相信大家写出代码没啥难度了。
- 初始,将起点加入集合 \(\mathbf{S}\),将相邻点加入集合 \(\mathbf{T}\)
- 找出集合 \(\mathbf{T}\) 中距离起点最近的点,加入集合 \(\mathbf{S}\),将其相邻点加入集合 \(\mathbf{T}\)
- 重复第二步,直到所有点都加入集合 \(\mathbf{S}\)
各种实现的区别,无非就是在第二步,找出距离起点最近的点时用了不同的方法。
节选一段 OI-Wiki 上的描述。
- 暴力:不使用任何数据结构进行维护,每次 2 操作执行完毕后,直接在集合中暴力寻找最短路长度最小的结点。2 操作总时间复杂度为 \(O(m)\),1 操作总时间复杂度为 \(O(n^2)\),全过程的时间复杂度为 \(O(n^2 + m) = O(n^2)\)
- 二叉堆:每成功松弛一条边 \((u,v)\),就将 \(v\) 插入二叉堆中(如果 \(v\) 已经在二叉堆中,直接修改相应元素的权值即可),1 操作直接取堆顶结点即可。共计 \(O(m)\) 次二叉堆上的插入(修改)操作,\(O(n)\) 次删除堆顶操作,而插入(修改)和删除的时间复杂度均为 \(O(\log n)\),时间复杂度为 \(O((n+m) \log n) = O(m\log n)\)。
- 优先队列:和二叉堆类似,但使用优先队列时,如果同一个点的最短路被更新多次,因为先前更新时插入的元素不能被删除,也不能被修改,只能留在优先队列中,故优先队列内的元素个数是 \(O(m)\) 的,时间复杂度为 \(O(m \log m)\)。
- Fibonacci 堆:和前面二者类似,但 Fibonacci 堆插入的时间复杂度为 \(O(1)\),故时间复杂度为 \(O(n\log n + m) = O(n \log n)\),时间复杂度最优。但因为 Fibonacci 堆较二叉堆不易实现,效率优势也不够大 [1](https://oi-wiki.org/graph/shortest-path/#fn:1) ,算法竞赛中较少使用。
- 线段树:和二叉堆原理类似,不过将每次成功松弛后插入二叉堆的操作改为在线段树上执行单点修改,而 1 操作则是线段树上的全局查询最小值。时间复杂度为 \(O(m \log n)\)。
代码实现提供 OI-Wiki 上的 C++ 版本。
// C++ Version
struct edge {
int v, w;
};
struct node {
int dis, u;
bool operator>(const node& a) const { return dis > a.dis; }
};
vector<edge> e[maxn];
int dis[maxn], vis[maxn];
priority_queue<node, vector<node>, greater<node> > q;
void dijkstra(int n, int s) {
memset(dis, 63, sizeof(dis));
dis[s] = 0;
q.push({0, s});
while (!q.empty()) {
int u = q.top().u;
q.pop();
if (vis[u]) continue;
vis[u] = 1;
for (auto ed : e[u]) {
int v = ed.v, w = ed.w;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
q.push({dis[v], v});
}
}
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号