【题解】Solution Set - NOIP2024集训Day43 博弈论
【题解】Solution Set - NOIP2024集训Day43 博弈论
https://www.becoder.com.cn/contest/5574
推荐一篇博客：https://www.cnblogs.com/linyihdfj/p/17447123.html
「ABC261Ex」Game on Graph
如果是 DAG 的话，直接跑一个 dp 应该就行。
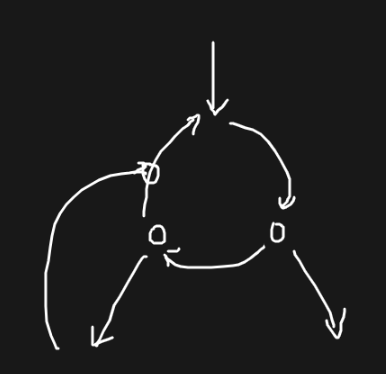
考虑破环，对于这样一个很 navie 的环。
分讨：
-
如果每个出口都是先手走到的。
-
如果这是一个偶环。
那么，答案应该是
INFINITY。 -
如果这是一个奇环。
-
-
如果不是每个出口都是先手走到的。
那么可以!@%!$!@#&*
考虑一条边会被走多次的条件：!@%!$!@#&*
BPU(Brain Processing Unit) 干烧了。
（27min passed...
做法可以看：https://www.luogu.com.cn/article/j08motvu
正确性可以看：https://www.luogu.com.cn/article/5z5cvnc9
聪慧的，又搞忘用「最短路松弛的方式」去转移带环的图上 dp 这个神秘的 trick 了。/kk
实际上，算法的本质是：
因为，我们最终的结果是要求最小值，所以其实转移就是求类似于一个最短路的东西。
如果两个转移方程都是取 \(\min\)，那么就是最短路了。
\(f_{u,0}\) 是可以转移，并正常入队的，这个的正确性其实是源于 dijkstra 的，取出来的时候就保证一定是取到真正的最小值了。
但是由于 \(f_{u,1}\) 的转移是取 \(\max\)，所以我们必须等她所有的转移都转移完了，保证了她取到了真正的最大值，才能入队来进一步转移。
注意必须是把所有出度为 \(0\) 点都先放在优先队列里面，然后再一起跑一边 dijkstra，不然 \(f_{u,0}\) 更新会错，进而导致 \(f_{u,1}\) 也错。
「AGC048D」Pocky Game
没救，没思路。
（10min passed...
https://www.luogu.com.cn/article/aet4fh76
相关证明：
结论：
-
因为我们可以一次性拿掉多出来的，这样一定不劣。
同时，如果第一堆足够的多，先手可以每次只拿一个，挨到后手一旦把除了第一堆的拿完，然后再一次性拿完。
推论：（一个不太严谨的证明
-
所以，占据一个很多的堆对双方都是至关重要的。
为了先占据这个堆，双方一开始肯定都是一堆一堆的拿，后面在一个一个的拿。（这其实就是题解里面说的那个过程。
反正，这个结论不算很好想啊。
转移方程里面当 \(a_r\ge g_{l+1,r}\) 的时候，要加上 \(f_{l,r-1}\) 是因为，我们在逼迫后手放弃可能让她制胜的 \(a_r\) 之后，还需要保证自己还需要让 \(a_l\) 在 \([l,r-1]\) 内取胜。
「BZOJ2688」Green Hackenbush
考虑一个 dp。
\(f_{i,j}\)：表示用 \(i\) 个节点构成的一棵树其 SG 值为 \(j\) 的概率。
有转移：
「POI1999」多边形之战
如果我们先把黑色三角形拎出来的话，剩余的图形应该之多是三个多边形。
我们设这三个多边形内分别被划分成的三角形个数为 \(x,y,z\)。
相当于，每次操作可以令这三个数中的一个 \(-1\)，然后谁先把其中两个数减成 \(0\)，谁就输。
显然可以转化为有向图游戏，暴力求 SG 的话应该是 \(O(n^3)\) 的。
感觉跟三个数的奇偶有点关系。
我们可以先对这三堆对 \(2\) 取模。（但是又感觉怪怪的。
（20min passed...
https://www.luogu.com.cn/article/r9xkv6qz
确实是奇偶但不是这么用的。题解还是应该是对所有的状态讨论（不过是对 \(2\) 取了模。
关键在于，如果让某个人一直拿到 110 的局面，那么她就必败。
https://www.luogu.com.cn/article/qlpc93gx
「中山市选2009」谁能赢呢？
一道经典的「二分图博弈」在棋盘问题上的应用。
