【题解】Solution Set - NOIP2024集训Day13 点分治、点分树
【题解】Solution Set - NOIP2024集训Day13 点分治、点分树
https://www.becoder.com.cn/contest/5476
「COCI 2018/2019」Deblo
看到异或就想到拆位。对于第 \(j\) 位。
如果 \(a_{\text{lca}(i,j)}\) 为 \(1\)，就是要在子树里面找两个当前位都为 \(1\) 的对数（为 \(0\) 同理），直接 dsu on tree 或者 点分治 就行了。（实际上也不需要，每个子树实际上只用开 \(2\log V\) 的空间，合并的时间复杂度相同，所以可以直接存下来。（dsu 甚至还多带一个 \(\log\)
「Hdu6643」Ridiculous Netizens
看到乘积，想到根号分治。
对于当前新加入的点的权值 \(a\)。
如果：
- \(a> \sqrt m\)，那么 \(\dfrac ma<\sqrt m\)，我们只需要记录乘积小于 \(\sqrt m\) 的那部分。
- \(a\le \sqrt m\)，那么对于每一个这样的 \(a\) 我们可以知道最大满足和她相乘小于等于 \(m\) 的值，而这样的值最多有 \(\sqrt m\) 个，所以直接存起来就好了。
Motivation：选取关键点 dp，减小时空。
跑一遍乘积和小于等于 \(x\) 的依赖于父亲的树背包。
或者转化到 dfn 序上 dp，具体可以参见：https://blog.csdn.net/Emm_Titan/article/details/121255055
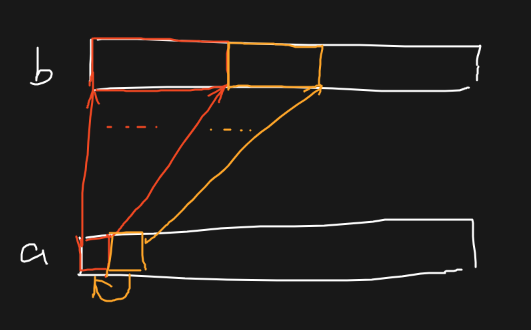
「ZJOI2015」幻想乡战略游戏
题意：求带权重心。支持动态修改权值。
考虑单个询问怎么做。
先随机走到一个点 \(u\)，考虑她的一个儿子 \(v\)，边权为 \(w\)，\(f_i\) 表示 \(i\) 的子树内 \(d\) 的和，\(sum\) 为整体 \(d\) 的和。
那么我们用 \(v\) 代替 \(u\) 的充要条件为：
（实际上一般的不带权的树重心也是这样推的。
显然我们不会走回头路，所以一旦我们往一个儿子走了，其她的儿子都没用了。
所以一旦走到一个儿子又是一个子问题
可以发现，答案的决策和边权并没有关系，也就是跟树的形态没有关系。
所以我们可以直接点分树。
但是我们不能像暴力那样直接算走过一条边之后答案的变化量，因为现在是走过的一条链，而链上面还要很多点，没法直接算贡献。
然后不会了。
好吧，正常的点分树就和度数有关了……因为题目保证了度数小于等于 \(20\) 所以我们暴力给每个儿子算答案，然后往会变小的那边走就行了。
每次算答案的话其实是一个点分树的典问题（【模板】点分树 | 震波 这应该算是加强版了），就是维护两个东西：
- \(x\) 子树中所有 \(d\) 对 \(x\) 的贡献；
- \(x\) 子树中所有 \(d\) 对 \(x\) 的父亲（点分树上）的贡献。
听说可以通过三度化，然后整个算法跟度数无关？
