【笔记】吉如一线段树
【笔记】吉如一线段树
吉如一论文(CQBZ内网,在 PDF 的 103 页
证明太复杂了,后面有时间来补。
1 区间最值操作
1.1 区间取 min(max),查询区间和
当前应该修改值为 \(x\);
维护区间最大值 \(mx\),最大值个数 \(t\),严格次大值 \(se\)。
如果走到一个区间上,如果:
- \(x\ge mx\),说明取min操作没用,直接 return;
- \(mx>x>se\),打标记,把 \(mx\) 改成 \(x\),再用 \((mx-x)\times t\) 更新区间和;
- 如果 \(x\le se\),暴力走两边递归下去。
时间复杂度:\(O(n\log n)\)。
1.2 区间取 min/max,区间加,查询区间和
和 1.1 差不多,区间加的时候直接加到 \(mx,se\) 就行了。
时间复杂度:\(O(n\log^2 n)\)。
但实际上上界很松,很难构造出 \(O(n\log^2 n)\) 的数据,运行效率一般在 \(O(n\log n)\)。
2 历史最值查询
2.1 区间加,查询区间历史最大值的最大值
先将一个节点的所有标记按顺序存在一个队列中。
同时每个节点维护:区间最大值 \(mx\),区间历史最大值 \(hmx\)。
每次弹出一个标记 \(t\) 的时候,\(mx\gets mx+t,hmx=\max(hmx,mx)\)。
然后我们考虑把这些标记合并起来:
其实后面这个 \(\max\left\{\sum\limits_i t_i\right\}\),就是加法标记的历史最值。
除了 \(mx,hmx\) 我们再维护:\(sumt\) 为标记的和,\(ht\) 为标记的历史最大值。
每次下放的时候:
d[p].ht = max(d[p].ht, d[p].sumt + d[fa].ht);
d[p].sumt += d[fa].sumt;
d[p].hmx = max(d[p].hmx, d[p].mx + d[fa].ht);
d[p].mx += d[fa].sumt;
2.2 区间赋值,区间加,查询区间历史最大值的最大值
较 2.1 而言,本问题只多了一个区间赋值操作。
考虑到对于一个区间如果进行了一次区间赋值的操作,那么后面全部的区间加都等价于区间区间赋值。
所以整个标记队列可以分成两部分:前面半截是区间加,后面半截是区间赋值。
加法标记按照 2.1 的方法处理。
赋值标记的历史最大值,显然就是所有的赋值标记取 \(\max\)。
记录这个值,最后跟历史最值取 \(\max\) 就行。
其实发现这就是 2.3 的弱化版,直接按照 2.3 的做法也行。
2.3 区间赋值,区间取max,区间加,查询单点历史最大值
(感觉也可以区间查询啊(?
三种操作可以合并成一个标记:设 \((a,b)\) 表示 \(x\gets\max(x+a,b)\)。
那么:
- 区间赋值 \(\Leftrightarrow (-\infty,b)\);
- 区间取 \(\max\Leftrightarrow (0,b)\);
- 区间加 \(\Leftrightarrow (a,-\infty)\)。
借用 2.1 的思路,考虑标记怎么合并。
假设原来的标记是 \((a_1,b_1)\),来了一个 \((a_2,b_2)\) 的标记那么可以合并为:\((a_1+a_2,\max(b_1+a_2,b_2))\)。
直接带入 \(x^\prime=\max(\max(x+a_1,b_1)+a_2,b_2)=\max(x+a_1+a_2,b_1+a_2,b_2)\)。
接着,我们考虑怎么给标记取 \(\max\)。
实际上每个标记都是两个一次函数拼起来的分段函数。
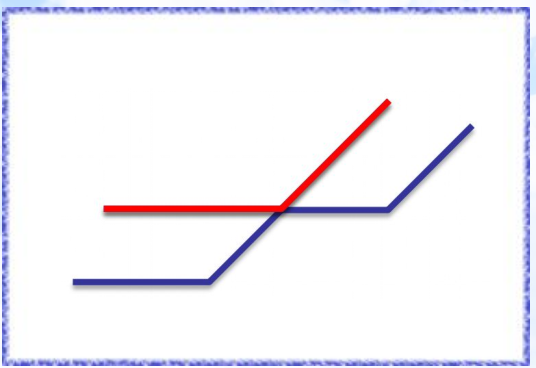
所以:\(\max((a_1,b_1),(a_2,b_2))=(\max(a_1,a_2),\max(b_1,b_2))\)。
2.3 总结
我们把上面两个流程 standardize 一下:
对于历史最值问在维护标记的时候,我们定义标记的合并 \(\circ\) 和广义 \(\max\)。
设当前标记为 \(t\),标记的历史最值为 \(ht\)。那么:
d[p].ht = max(d[p].ht, d[fa].ht ○ d[p].t)
d[p].t = d[fa].t ○ d[p].t
注意:这个 \(\circ\) 相当于是函数的复合,\(f\circ g\Leftrightarrow f(g(x))\) 相当于先是后面的作用,再前面的作用,所以合并的时候先是后面的再是前面的。
因为儿子的标记先被打上(不然后打儿子标记的时候一定会先吧父亲的下放),所以一定先是儿子再是前面的。
标记维护好了,最值和历史最值就很好求得了。
d[p].hmx = max(d[p].hmx, d[fa].ht ○ d[p].mx)
d[p].mx = d[fa].t ○ d[p].mx
最后注意一下顺序,只要上面两个代码框里面的两条不写反就行。
3 历史和查询
3.1 区间加,查询区间历史版本和的和
结论:
设当前标记为x,标记的历史版本和为y,历史修改次数为z
区间和为a,区间历史版本和的和为b,区间长度为len
那么:
son.b+=son.a*fa.z+fa.y*son.len
son.a+=fa.x*son.len
son.y+=son.x*fa.z+fa.y
son.z+=fa.z
son.x+=fa.x


