【笔记】快速傅里叶变换
0 约定
- \(\exp(x)=e^x\)。
- 有些地方标注有
?,系本人不太能保证严谨性的部分。
1 复数 (Complex)
1.1 三种形式
-
代数形式:\(z=a+bi\),其中 \(a,b\in\mathbb R\)。
-
三角形式:\(z=r(\cos\theta+i\sin\theta)\),其中 \(r=\sqrt{a^2+b^2}\)(\(a,b\) 是在代数形式中定义的)。
-
指数形式:\(z=r\cdot e^{i\theta}\)。
根据 欧拉公式:
\[e^{ix}=\cos x+i\sin x,x\in\mathbb C \]令 \(x=\theta\),再带入三角形式中,即可得指数形式。
1.2 单位根 (unit root)
对于方程 \(x^n=1\),在复数意义下,她有 \(n\) 个解,我们称这 \(n\) 个解都是 单位根 (unit root)。
设 \(\boxed{\omega_n=\exp\frac{2\pi i}n}\),则这 \(n\) 个单位根可以表示为 $ {\omega_n^k\mid k=0,1\cdots,n-1} $。
在复平面中,\(n\) 次单位根把单位圆 \(n\) 等分。
1.2.1 性质
-
\(\omega_n^n=1\)
证:\(\omega_n^n=\exp\left(\dfrac{2\pi i}nn\right)=(\exp\pi i)^2=(-1)^2=1\)
-
\(\omega_n^k=\omega_{pn}^{pk}\)
\(\omega\) 的上下标同乘 \(p\),相当于 \(\exp\) 后面的分子分母同乘 \(p\)。
-
\(\omega_{2n}^{k+n}=-\omega_{2n}^{k}\)
几何理解:这实际上相当于将单位园 \(2n\) 等分,次数 \(+n\) 相当于在复平面中,这两个点关于原点对称,故而她们互为相反数。(?
证:\(\omega_{2n}^{k+n}=\exp\dfrac{2\pi i(k+n)}{2n}=\exp\left(\dfrac{2\pi ik}{2n}+\dfrac{2\pi in}{2n}\right)=-\exp\left(\dfrac{2\pi ik}{2n}\right)=-\omega_{2n}^k\)
2 快速傅里叶变换 (Fast Fourier Transform)
FFT 可以在 \(O(n\log n)\) 的时间复杂度内,计算多项式乘法,优于暴力的 \(O(n^2)\)。
2.1 定义
对于一个多项式 \(f(x)\),定义傅里叶变换为:
傅里叶变化本质上可以理解为一种「从一个多项式到一个 \(n\) 维向量的映射关系」,将多项式的系数表示转化为点值表示。(?
2.2 求解
2.2.1 引入(不太重要
考虑如何计算 \(\sum\limits_{i=0}^na_ix^i\)。
一般的方法是,枚举 \(i\),然后维护 \(x^i\) 的值 \(k\),再将 \(a_i\) 与 \(k\) 相乘并累加。精细统计的话,这样应该需要 \(2n\) 次乘法。
另一种办法是:
如果是这样计算,总共其实只需要 \(n\) 次计算。(似乎没什么用
2.2.2 思想
不失一般性的,我们令 \(n=2^p(p\in\mathbb N)\)(如果 \(n\) 不足 \(2^p\),可将更高位的系数视作 \(0\)。
借用上述思想,对于一个多项式 \(f(x)\),我们可以做如下的变换,即将 \(f(x)\) 按 \(x\) 次数的奇偶分开:
令 \(f_0(x)=a_0+a_2x^1+\cdots+a_{n-2}x^{n/2-1}\),\(f_1(x)=a_1+a_3x^1+\cdots+a_{n-1}x^{n/2-1}\)。
代回原式:
所以我们有:
以及:
然后我们惊奇的发现,这两个式子只有系数差别,而且 \(n\) 的规模每次减半。这就意味着我们可以在 \(O(n\log n)\) 的时间复杂度内递归求解出 \(f(\omega_n^k)\) 其中 \(k=0,1,\dots,n-1\),即求出 \(\mathcal F(f(x))\)。
而上面最后推出的式子被称做:蝴蝶操作 (Butterfly Operation)。下面这张图形象地展示了「蝴蝶」的含义:
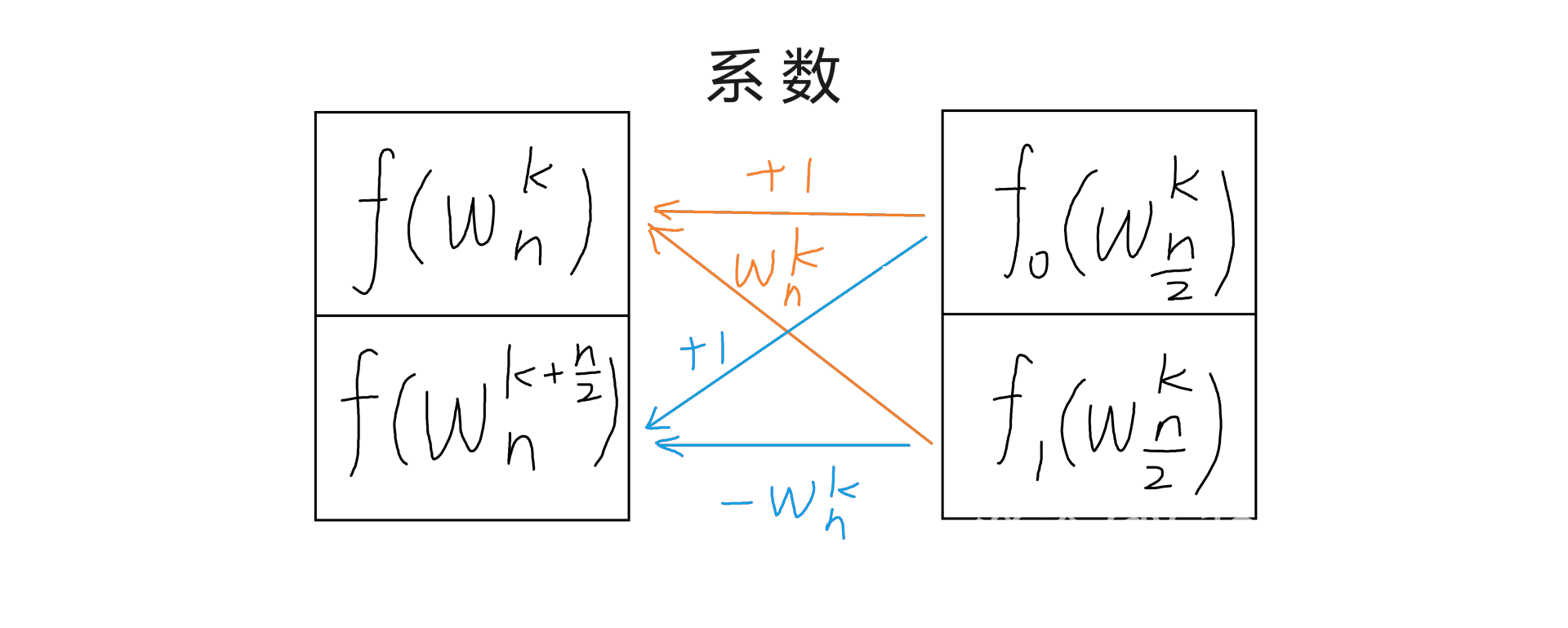
2.2.3 实现
通过递归我们可以轻易的模拟出上述过程,为减少常数下介绍一种非递归版本。
画出递归树,如下图,并按照下图的方式给每层的 \(f\) 编号:

我们发现,最底层的 \(f\) 的二进制下标反转过来并转换成十进制,就等于她对应 \(a\) 的下标。
所以我们可以直接预处理出最底层的 \(f\),然后自下而上递推回来。(具体实现可以参考 4.1 Code 中的 \(r\)。
3 快速傅里叶逆变换 (Inverse Fast Fourier Transform)
3.1 定义
设 \(f^\prime\) 为进行了快速傅里叶变化后的点值,即 \(\mathcal F(f(x))\)。
现在考虑还原为原来的系数数列。这样的操作被称之为 快速傅里叶逆变换 (Inverse Fast Fourier Transform)。
推导过程比较复杂,这里直接给出结论:
4 优化多项式乘法
那么傅里叶变换的优势在哪呢?这就要问点值表达了。
由于是用点值表示多项式,两个多项式相乘,显然就是每个点的虚数相乘。
最后再做一次逆变换,相当于插值,就可以还原回最终结果了。
4.1 Code
#include <bits/stdc++.h>
using namespace std;
const int N = 4e6 + 5, logN = 20;
const double PI = acos(-1);
int n, m, lim, len, r[N];
struct Complex {
double a, b;
Complex operator + (Complex x) { return {a+x.a, b+x.b}; }
Complex operator - (Complex x) { return {a-x.a, b-x.b}; }
Complex operator * (Complex x) { return {a*x.a-b*x.b, a*x.b+b*x.a}; }
} a[N], b[N], c[N];
void fft (Complex *f, int sign) {
for (int i = 0; i < lim; i++)
if (i < r[i]) swap(f[i], f[r[i]]);
for (int mid = 1; mid < lim; mid<<=1) {
Complex o = {cos(PI/mid), sign*sin(PI/mid)};
for (int R = mid<<1, j=0; j < lim; j += R) {
Complex p = {1, 0};
for (int k = 0; k < mid; k++) {
Complex f0 = f[j+k], f1 = f[j+k+mid];
f[j+k] = f0 + p*f1;
f[j+k+mid] = f0 - p*f1;
p = p*o;
}
}
}
}
int main () {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for (int i = 0, x; i <= n; i++) cin >> x, a[i] = {x*1.0, 0};
for (int i = 0, x; i <= m; i++) cin >> x, b[i] = {x*1.0, 0};
for (lim=1, len=0; lim <= n+m; lim<<=1, len++);
for (int i = 0; i <= lim; i++)
r[i] = (r[i>>1]>>1)|((i&1)<<(len-1));
fft(a, 1), fft(b, 1);
for (int i = 0; i <= lim; i++) c[i] = a[i]*b[i];
fft(c, -1);
for (int i = 0; i <= n+m; i++)
cout << ((int)(c[i].a/lim+0.5)) << ' ';
return 0;
}
5 例题
「BZOJ4503」两个串
\(n=|S|,m=|T|\)
首先将 \(\{?,a,b,\dots,z\}\to\{0,1,2,\dots,26\}\)。然后将 \(T\) reverse 下。
在 \(s\) 的第 \(i\) 匹配成功,可以转换为:
平方是为了防止负数可能的抵消,如果是绝对值不能化简。
然后暴力拆开看下:
然后发现,这就是两个卷积和一个普通累加相加,fft 加速算即可。
「ZJOI2014」力
Warning: 不同于题面,下面的数组均从 \(0\) 开始标号。
令:
于是:
考虑分开计算 \(A,B\)。
再令:
由于 \(p_0=0\),于是 \(i=j\) 可以被纳入运算,而不造成影响。
再把 \(q\) reverse 下,令作 \(q^\prime\)。
于是:
又令:\(t=n-i-1\)。
有:
fft 加速算即可。
万径人踪灭
假定 \(a_i=0(i\ge n)\)。
令:\(t0=2i,t1=2i+1\\\)。
设:
- \(f_i\) :以 \(i\) 为对称中心,两边最多能匹配的对数(包括自己);
- 而 \(g\) 是枚举分割线。
则有
然后答案就是:
其中 \(res\) 为字符串中回文串个数,这个可以用 Manacher 算。
\(f,g\) 卷积算完之后加上后面的那部分即可。
「BZOJ 3771」Triple
「Luogu5488」差分与前缀和
算一次的前缀:
考虑每个 \(a[i]\) 对 \(Ans\) 的贡献。

