【算法】平衡树
参考资料
- OI-Wiki: *衡树
- Chanis: 不用旋转的treap?——fhq treap
- 曦行夜落: 浅析Treap——*衡树
- ctjcalc: 【数据结构】FHQ Treap 详解
- 奇思录: 深入理解伸展树(splay tree)
- 【朝夕的ACM笔记】数据结构-Splay Tree
- Seaway-Fu: Splay算法详解
- 樱雪喵: Splay 详细图解 & 轻量级代码实现
概念
前置:二叉搜索树
二叉搜索树是一种满足 左子树上所有权值 \(<\) 根节点上的权值 \(<\) 右子树上所有权值 的二叉树。根据它的结构,可以利用二叉搜索树来进行插入,删除,查询最值,查询某个数的排名,查询第 \(k\) 个数,查询前驱,查询后继。
- 插入
令当前访问的节点为 \(cur\),要插入的值为 \(v\),分为以下几种情况讨论:
- \(tree[cur].v=v\),令 \(tree[cur].cnt\) 表示当前节点的值出现了几次,直接令其加一。
- \(v<tree[cur].v\),根据二叉搜索树的定义,此时要插入的位置应是 \(cur\) 的左子树。
- \(v>tree[cur].v\),根据二叉搜索树的定义,此时要插入的位置应是 \(cur\) 的右子树。
- \(cur\) 为空,那么这就是我们要插入的位置,新建一个节点即可。
- 删除
令要删除的节点是 \(cur\),分为以下几种情况讨论:
- \(cur\) 有多个,即 \(tree[cur].cnt>1\),只需要将其减一。
- \(tree[cur]\) 为叶子节点,直接删掉。
- \(tree[cur]\) 只有一个儿子,直接把它的儿子提上来。
- \(tree[cur]\) 有两个儿子,将它左子树里面的最大值或者右子树里面的最小值提上来。
- 查询最值
根据二叉搜索树的定义,树中的最小值就是最靠左的那个节点,树中的最大值就是最靠右的节点。
- 查询某个数的排名
假设要查询的数是 \(x\) 且保证 \(x\) 已经在二叉搜索树里面了。从根节点开始搜,令 \(cur\) 表示当前所在树节点,分为以下几种情况讨论:
- 若 \(x<tree[cur].v\),那么 \(x\) 在左子树内,直接递归下去。
- 若 \(x\) 恰为 \(tree[cur].v\),直接返回当前节点的左子树大小。
- 若 \(x>tree[cur].v\),那么 \(x\) 在右子树内,递归下去,并将答案加上左子树大小和 \(tree[cur].cnt\)。
这实际上查询的是小于 \(x\) 的个数,最后的答案还需要再加一。
- 查询第 \(k\) 个的数
与上面的类似,假设要查第 \(k\) 小的数是多少,令 \(cur\) 表示当前所在树节点,分为以下几种情况讨论:
- 若左子树的大小 \(\ge k\),继续在左子树中找第 \(k\) 小的数。
- 若左子树的大小 \(+ tree[cur].cnt\ge k\),那么 \(tree[cur]\) 就是第 \(k\) 小的数。
- 否则,继续在右子树中找第 \(k-\) 左子树大小 \(-tree[cur].cnt\)。
- 前驱和后继
这两个类似,有两种思路处理。令要查询的是 \(x\) 的前驱/后继。
第一种是查询 \(x\) 的排名,将它调整为前驱/后继的排名,然后再查第 \(k\) 小的数。
第二种是用二叉搜索树的性质,前驱就是 \(x\) 的左子树里面最靠右的点或者是它的父节点(\(x\) 为右儿子),后继就是 \(x\) 的右子树内最靠左的点或者是它的父节点(\(x\) 为左儿子)。
不难发现,二叉搜索树的时间复杂度和它的树高有关,当二叉搜索树退化成链的时候,时间复杂度也从 \(O(\log_2 n)\) 退化到了 \(O(n)\)。
*衡树
我们显然不希望时间复杂度退化到线性,于是我们就需要*衡一下它的树高,使得时间复杂度尽量为 \(O(\log_2 n)\)。在二叉搜索树中,常见的*衡性是指每一个节点的左子树高度和右子树高度相差不超过 \(1\)。
这种可以有*衡性的二叉搜索树就是*衡二叉搜索树,也是常说的*衡树。
Treap
treap = tree(树)+ heap(堆),它是一种既有树的性质(见上),又有堆的性质(每一个点的值都大于/小于父节点的值,编者一般在这里用大根堆)的数据结构。
因此,我们维护两个值,一个树值 \(v\),一个堆值 \(rnd\)。前者维护二叉搜索树的性质,后者看变量名就知道是随机给出的。根据这个随机给出的堆值,期望的树高也是接* \(\log_2 n\) 的。这是由于我们可以把这个随机的堆值看做是一个随机的插入顺序,从而达到弱*衡性。
为了让 treap 同时具有树和堆的性质,我们可以使用两种方法,一种是有旋 treap,它是通过旋转来维护*衡的;另一种是无旋 treap,又称 fhq treap,它是通过分类和合并来维护*衡的。
有旋 treap
- 旋转
核心操作是上文提到的旋转操作,分为左旋和右旋,这是一对相互操作。
旋转操作是在不影响将与旋转方向相反的子树变为根节点,将原来的根节点变为与旋转方向相同的子节点。形象一点可以理解为把原来根节点的一个子树给提了上来,然后再维护搜索树的性质。
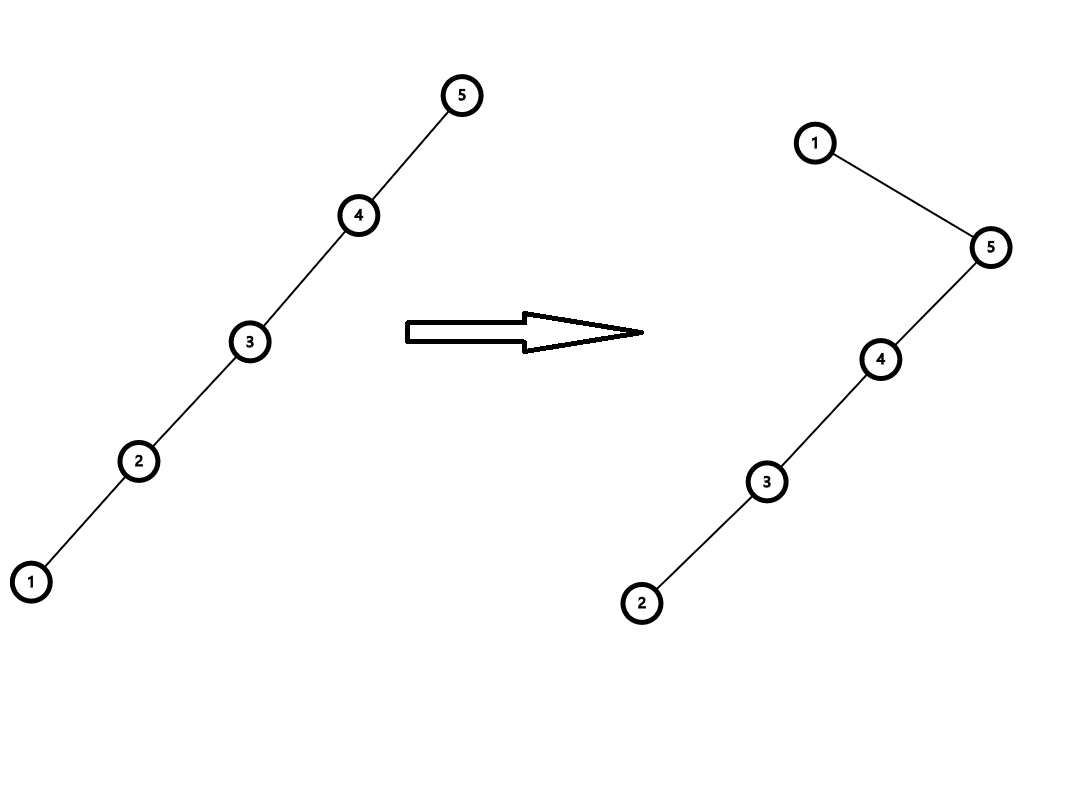
举个例子,现在这棵树长这样:
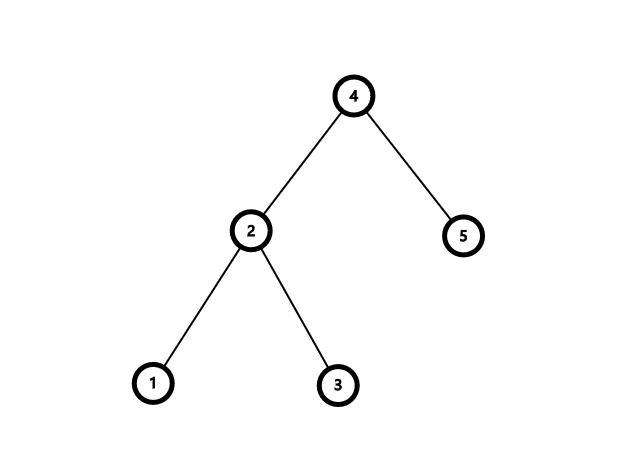
根据这棵树的搜索树的性质可以得出 \(1<2<3<4<5\)。现在我们考虑进行右旋操作。先把左子树给提上来。
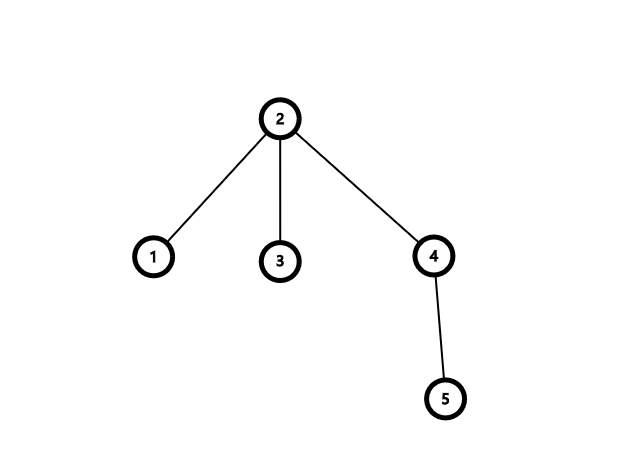
这时候这棵树不仅不满足二叉搜索树的性质,甚至它已经不是一颗二叉树了。我们发现由于 \(4>3>2\),所以 \(3\) 实际的位置应该放在 \(4\) 的左子树里面,如下图。
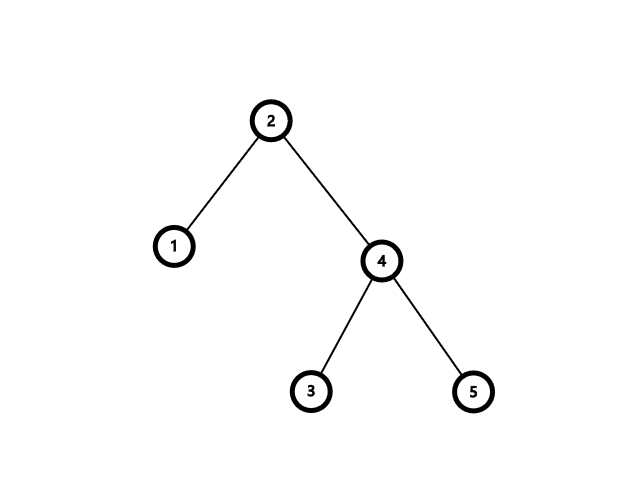
这就进行了一次右旋操作。若是在操作后的图上再进行一次左旋操作便得到了原图。考虑总结一下旋转操作,以左旋为例。令当前节点为 \(cur\),右儿子为 \(v\)。由于旋转过后 \(v\) 的左儿子要是 \(cur\),所以先把 \(v\) 的左儿子给拿出来,然后根据搜索树的性质,\(v\) 的左儿子的权值一定都大于 \(cur\) 的权值,所以把它放在 \(cur\) 的右儿子中(原来的右儿子为 \(v\),但旋转过后右儿子便空了,所以这样的操作不会与原来的儿子冲突)。最后再把 \(cur\) 放到 \(v\) 的左子树中即可。
根据上面的总结,我们可以写出以下代码:
void rotate(int &cur,int x){//为方便理解,下面注释的变量命名与上面解释的一致
int nr=tree[cur].son[x^1];//现在的根节点应该是与旋转方向相反的子节点 v
tree[cur].son[x^1]=tree[nr].son[x];//cur 的与旋转方向相反的子树应该放 v 与旋转方向一致的儿子
tree[nr].son[x]=cur;//再把 cur 放入 v 与旋转方向一致的儿子
pushup(cur); pushup(nr);//pushup 的意思是更新节点的子树大小
cur=nr;//新根节点是 v
}
- 插入
基本的插入操作和普通二叉搜索树的插入操作类似。需要注意的是如果插入的子节点 \(v\) 的堆值大于 \(cur\) 的堆值时,考虑到我们维护的是大根堆,那么 \(v\) 就应该取代 \(cur\) 成为新的根节点,同时还要保证树的性质。因此此处会进行旋转操作,并与 \(v\) 在 \(cur\) 的子树方向相反。
void ins(int &cur,int x){
if(cur==0){//节点为空,新建节点
cur=++cnt;
size[cur]=num[cur]=1;
tree[cur].v=x;
rnd[cur]=rand();//随机一个堆值
return;
}
if(tree[cur].v==x){//如果已经有了这个权值的节点
num[cur]++;
size[cur]++;
return;
}
int d;
if(x>tree[cur].v) d=1;//插到右子树中
else d=0;//插到左子树中
ins(tree[cur].son[d],x);
if(rnd[cur]<rnd[tree[cur].son[d]]) rotate(cur,d^1);//维护堆的性质
pushup(cur);
}
- 删除
如果当前要删除的节点为 \(cur\),进行以下几种分类讨论:
- \(cur\) 为叶子节点,直接删掉。
- 如果有左儿子,没有右儿子,进行一次右旋操作让 \(cur\) 转到右子树里面去。不难发现旋转后的 \(cur\) 一定是叶子节点,转化为类型 \(1\)。
- 如果有右儿子,没有左儿子,进行左旋操作,并转化为类型 \(1\)。
- 如果两个儿子都在,选两个儿子里面堆值较大的当新根节点,即进行一次对应的旋转操作,然后去另一个子树内递归。
void del(int &cur,int x){
if(cur==0) return;
if(x<tree[cur].v) del(tree[cur].son[0],x);
else if(x==tree[cur].v){
if(tree[cur].son[0]==0&&tree[cur].son[1]==0){//类型 1
size[cur]--;
num[cur]--;
if(num[cur]==0) cur=0;
}
else if(tree[cur].son[0]==0&&tree[cur].son[1]!=0){//类型 2
rotate(cur,0);
del(tree[cur].son[0],x);
}
else if(tree[cur].son[0]!=0&&tree[cur].son[1]==0){//类型 3
rotate(cur,1);
del(tree[cur].son[1],x);
}
else{//类型 4
int d;
if(rnd[tree[cur].son[0]]>rnd[tree[cur].son[1]]) d=1;
else d=0;
rotate(cur,d);
del(tree[cur].son[d],x);
}
}
else del(tree[cur].son[1],x);
pushup(cur);
}
- 其余操作
与普通二叉搜索树类似。
无旋 treap
- 分裂
与有旋 treap 中的旋转类似,分裂在无旋 treap 也同样是核心操作之一。分裂有两种,一种是按权值分裂,另一种是按排名分裂。按权值分裂主要目的是将一个 treap 分成两个 treap,一个 treap 中的所有点的值都小于等于一个给定的值 \(v\),另一个 treap 中的所有点的值都大于 \(v\)。
具体地,令当前访问的节点为 \(cur\),如果 \(cur\) 的值小于等于 \(v\),那么 \(cur\) 和它的左子树都一定属于第一个 treap,并且它右子树的一部分可能也属于第一个 treap,我们便递归分裂右子树。\(cur\) 的值大于 \(v\) 的时候同理。
void split(int cur,int &x,int &y,int k){//x,y 表示分裂后的两颗 treap 中现在遍历到的点
if(cur==0){
x=y=0;
return;
}
if(tree[cur].v<=k){
x=cur;//当前 x 这个 treap 中遍历到的点是 cur
split(tree[cur].rt,tree[cur].rt,y,k);//在 cur 的右子树中找同属第一个 treap 的部分,并将其赋为 cur 新的右子树
}
else{
y=cur;
split(tree[cur].lt,x,tree[cur].lt,k);
}
pushup(cur);
}
按排名分裂类似
void split(int cur,int &x,int &y,int k){
if(cur==0){
x=y=0;
return;
}
if(tree[tree[cur].lt].siz+1<=k){
x=cur;
split(tree[cur].rt,tree[cur].rt,y,k-tree[tree[cur].lt].siz-1);
}
else{
y=cur;
split(tree[cur].lt,x,tree[cur].lt,k);
}
pushup(cur);
}
- 合并
无旋 treap 中的合并操作一般来说都是从同一个 treap 中分裂出去的两个 treap,因此一个 treap 中的所有元素的值都会小于另一个 treap 中所有元素的值。它的作用和有旋 treap 中的旋转操作类似,都是在满足树性质的时候通过合并再满足堆的性质,并且不改变树的性质。
令 \(x\) 中的所有值都小于 \(y\) 中的所有值,由于 treap 已经有序,我们只需要比较堆值来看谁放在上面。如果 \(rnd[x]\ge rnd[y]\) (大根堆),我们便将 \(x\) 作为根节点并保留它的左子树,递归再把它的右子树和 \(y\) 合并。同理,如果 \(rnd[x]<rnd[y]\),我们便将 \(y\) 作为根节点并保留它的右子树,递归再把它的左子树和 \(x\) 合并。
int unionn(int x,int y){
if(x==0) return y;
if(y==0) return x;
if(rnd[x]>=rnd[y]){
tree[x].rt=unionn(tree[x].rt,y);
pushup(x);
return x;
}
else{
tree[y].lt=unionn(x,tree[y].lt);
pushup(y);
return y;
}
}
- 插入
我们把整棵 treap 分成 \(\le k-1\) 和 \(> k-1\) 的两个部分,然后新建一个值为需要插入的 \(k\) 的节点,暴力将这个节点和分裂之后的两个部分依次合并即可。为什么要分裂之后才能合并,而不是直接将这个节点合并进去的原因在合并中其实便已经阐述,我们必须满足要合并的两个 treap \(x\),\(y\) 满足 \(x\) 中的所有权值全部小于 \(y\),如果不进行分裂,便不能满足这个前提条件,也就不能进行合并操作。
void ins(int cur,int k){
int x=0,y=0;
split(root,x,y,k-1);
cur=++cnt;
tree[cur].lt=tree[cur].rt=0;
size[cur]=1;
rnd[cur]=rand();
tree[cur].v=k;
root=unionn(x,unionn(cur,y));
}
- 删除
我们将 treap 分裂成 \(\le k\) 和 \(>k\) 的两个部分,再将 \(\le k\) 的部分分裂成 \(\le k-1\) 和 \(>k-1\) 的两个部分,就可以满足其中一个 treap 一定都是权值为 \(k\) 的节点。然后把这个 treap 的左右子树直接合并起来而不合并根节点,就删除了根节点这个值为 \(k\) 的点。最后再合并回去即可。
void del(int k){
int x=0,y=0,z=0;
split(root,x,z,k);
split(x,x,y,k-1);
y=unionn(tree[y].lt,tree[y].rt);
root=unionn(unionn(x,y),z);
}
- 查询某个数的排名
将 treap 分裂成 \(\le k-1\) 和 \(>k-1\) 的两个部分,\(k\) 的排名就是第一个 treap 的大小再加一。
int query_r(int k){
int x=0,y=0;
split(root,x,y,k-1);
int rk=size[x]+1;
unionn(x,y);
return rk;
}
- 查询第 \(k\) 个的数
常见的有两种写法,第一种写法与二叉搜索树的遍历方式类似。如果左子树的大小大于等于 \(k\),那么递归左子树;如果左子树的大小加上 \(1\) 恰为 \(k\),那么此时遍历到的点就是第 \(k\) 个数;否则遍历右子树。
int query_n(int cur,int k){
if(size[tree[cur].lt]+1==k) return tree[cur].v;
if(size[tree[cur].lt]>=k) return query_n(tree[cur].lt,k);
else return query_n(tree[cur].rt,k-size[tree[cur].lt]-1);
}
事实上,插入和删除操作也可以用二叉搜索树的方式实现,只是不是特别常见。
第二种写法是按照值域分裂,与删除操作类似,先分成排名 \(\le k\) 和 \(>k\) 的两个部分,再将第一个 treap 分成 \(\le k-1\) 和 \(>k-1\) 的两个部分,后面这个 treap 中任意一个点的权值就是第 \(k\) 个数。
int query_n(int k){
int x=0,y=0,z=0;
split(root,x,z,k);
split(x,x,y,k-1);
int ansi=tree[y].v;
root=unionn(unionn(x,y),z);
return ansi;
}
- 前驱和后继
前驱和后继实现方式类似,因此这里只阐述前驱。先将 treap 分裂成 \(\le k-1\) 和 \(>k-1\) 的两部分,\(k\) 的前驱一定在第一个 treap 中。因此在第一个 treap 中输出最大的,即第 \(tree[cur].siz\) 个数即可,或者按照二叉搜索树的方式不断地走第一个 treap 的右儿子。
int pre(int cur,int k){
int x=0,y=0;
split(root,x,y,k-1);
cur=x;
while(tree[cur].rt!=0) cur=tree[cur].rt;
unionn(x,y);
return tree[cur].v;
}
int suc(int cur,int k){
int x=0,y=0;
split(root,x,y,k);
cur=y;
while(tree[cur].lt!=0) cur=tree[cur].lt;
unionn(x,y);
return tree[cur].v;
}
应用
区间操作
一般而言,无旋 treap 相较于有旋 treap 的优势便是可以进行区间操作。运用无旋 treap 进行区间操作时,常见的一种操作时将 treap 分成 \([1,l-1]\),\([l,r]\),\([r+1,n]\) 的三部分,然后再对 \([l,r]\) 进行操作。
经典例题有【模板】文艺*衡树,下面对此题进行无旋 treap 区间操作的分析。
考虑维护一个 treap 满足它的中序遍历是有序的,可以参照笛卡尔树的单调栈建树方法来实现。具体地,若当前遍历到的节点时 \(cur\),由于插入顺序递增,因此它一定是在这个 treap 的最右端。我们用单调栈维护最右边这条链,如果栈顶元素的 \(rnd\) 要小于 \(cur\) 的 \(rnd\) 值(维护的是一个大根堆),那么就把这个元素弹出,直到栈顶元素的堆值大于 \(cur\) 的堆值。弹出的元素维护之前的顺序不变放入 \(cur\) 的左子树里即可。
区间翻转的时候按照最开始的操作分成三个部分,把中间 \([l,r]\) 的部分的每个节点的左右儿子节点都交换一下,这样的时间复杂度是 \(O(n\log_2n)\),十分的慢。因此考虑打上懒标记表示这个子树内的所有节点的左右儿子都要交换。打上懒标记后,在每次分裂,合并或者最后的输出时都要下传懒标记。
可持久化
一般而言,这里的可持久化也是指可持久化无旋 treap。
和普通的无旋 treap 差不太多,唯一的不同就是在合并和分裂的时候要新开节点,并用 \(root_i\) 表示第 \(i\) 个历史版本的根的编号。
Splay
Splay 是一种通过伸展操作不断地将操作节点旋转到根节点,同时对这条路径上的所有节点都进行了优化,使得树趋*于*衡。
这里推荐一个视频来了解 Splay 的伸展操作:凿壁蹭网: 来感受一下Splay的旋转风暴吧!
旋转
splay 的旋转与有旋 treap 的旋转相似,有左旋和右旋一说。不同的点一是在于 Splay 还要维护节点的父亲这一信息导致的多出的处理,二是 treap 左右旋实际上是把自己的左右儿子给旋上来,而 splay 则是把自己旋到父节点的位置上。
比较懒,就把有旋 treap 的图给偷过来了。

假设我们现在要把节点 \(1\) 旋上去,不难得出,旋上去的图应该长下面这样:(怎么还是要画图
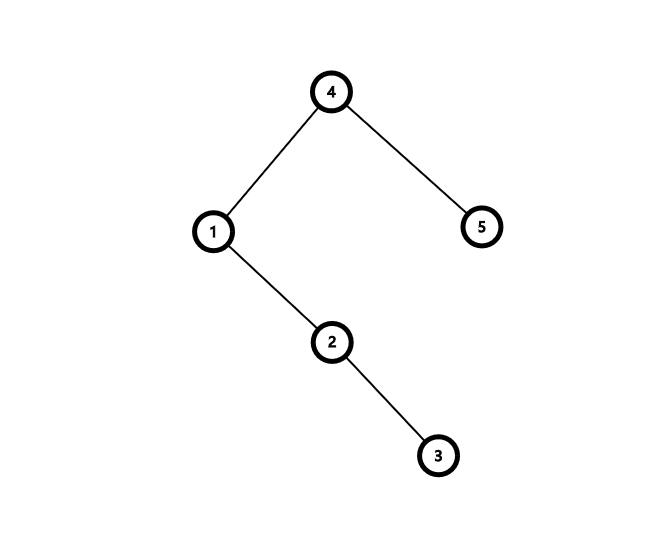
发现更改的有以下几个地方:
- 节点 \(1\) 的右儿子(由空到节点 \(2\))
- 节点 \(2\) 的左儿子(由节点 \(1\) 到空)
- 节点 \(4\) 的左儿子(由节点 \(2\) 到节点 \(1\))
当然变化的地方还有对应节点的父亲的信息,但可以在更改儿子信息时顺便维护,在此便不多过多赘述。
为了方便,处理这些信息的顺序我们考虑从下到上。以下情况假设 \(x\) 是其父节点 \(fx\) 的左儿子。
- 将 \(x\) 的右子树给 \(fx\) 的左子树:旋转后 \(x\) 的右子树必须放 \(fx\),而 \(fx\) 的左子树又会从 \(x\) 变为空。又根据二叉搜索树的性质,\(x\) 的右子树一定会比 \(fx\) 的值要小,因此需要把 \(x\) 的右子树给 \(fx\) 的左子树。
- 将 \(x\) 的右子树赋为 \(fx\)。
- 将 \(ffx\) (\(fx\) 的父亲)的对应 \(fx\) 原在的儿子位置改为 \(x\)。
实现如下:
void rotate(int x){
int fx=fa[x],gf=fa[fx];
int d=get(x);//get 函数表示 x 是 fx 的左儿子还是右儿子
tree[fx].son[d]=tree[x].son[d^1];//将 x 的与 d 相反方向的子树给 fx 与 d 相同方向的子树
if(tree[x].son[d^1]) fa[tree[x].son[d^1]]=fx;//同时维护父亲信息。要判不为空的原因是防止之后访问到空节点后还能继续进行不合法操作
tree[x].son[d^1]=fx;//将 fx 放入 x 的与 d 相反方向的子树
fa[fx]=x;//同时维护父亲信息
fa[x]=gf;//将 x 的父亲改为原来的祖先
if(gf) tree[gf].son[fx==tree[gf].son[1]]=x;//注意这里必须判 fx==tree[gf].son[1] 而不能是 get(fx),原因是 fx 的父亲已经更改为 x 了
pushup(fx);//先维护 fx,也就是当前较深节点的信息
pushup(x);//再维护深度较浅节点的信息
}
伸展
Zig-Zag / Zag-Zig
splay 的一大特点就是每一次的操作点,在操作过后一定要旋到根节点。而维护这个操作不难想到一直将 \(x\) 往上旋,直到它是根节点。如下图,把节点 \(1\) 进行多次这样的操作,最后得到的图是这样的:
树的高度不变,如果下一次我们要将 \(2\) 给旋到根节点上去,也同样需要 \(5\) 次操作。这样的效率十分的慢,原因是树退化成链了,而本次旋 \(1\) 到根节点的操作又不能改变树的形态。
因此我们只有在 \(x\),\(fa[x]\),\(fa[fa[x]]\) 不在同一条直线上时进行旋两次 \(x\) 的操作,这种操作也被称为 Zig-Zag / Zag-Zig。
Zig / Zag
当 \(fa[x]\) 是根节点的时候进行操作,直接一步把 \(x\) 给旋到跟节点上去。
Zig-Zig / Zag-Zag
在上面已经说过,当树是一条链(如果只考虑 \(x\) 及其父亲和祖父的情况的话,就是 \(x\),\(fa[x]\),\(fa[fa[x]]\) 共线)的时候,运用 Zig-Zag 后不能改变树的深度,从而影响效率。因此我们定义一次 Zig-Zig 操作为当 \(x\),\(fa[x]\),\(fa[fa[x]]\) 共线时,先旋 \(fa[x]\),再旋 \(x\)。对于上面图示里的那张图,旋转顺序为 \(2,1,4,1\),最后旋转的结果如下:
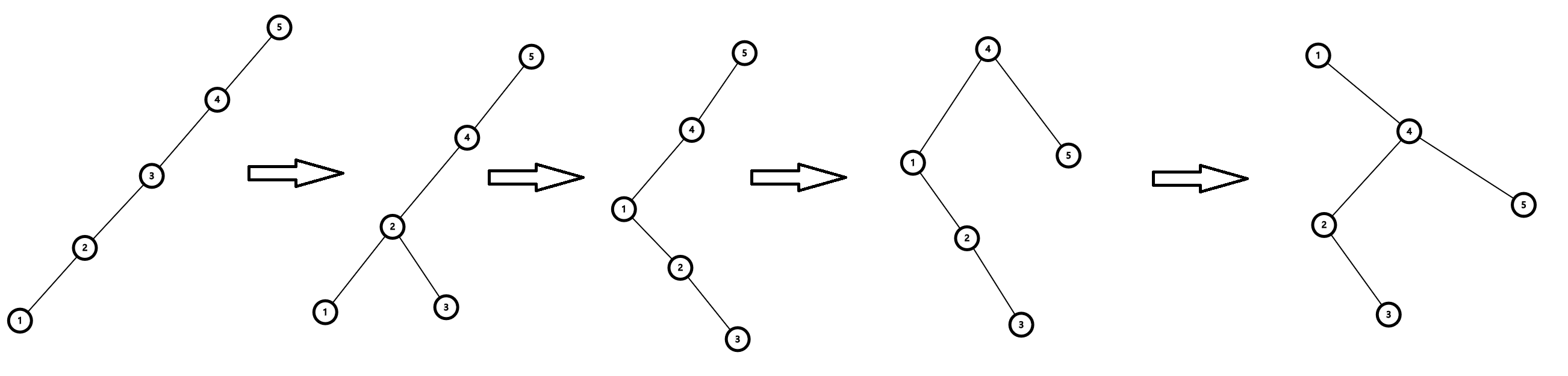
根据上面这三种操作,我们可以写出 Splay (伸展)代码:
void splay(int cur){
int fx=fa[cur];
while(fx){
//由于 zig,zig-zig,zig-zag 操作都有共同的旋转 x 的部分,因此可以把它提出来
if(fa[fx]){//没有祖父就直接进行 zig 操作
if(get(cur)==get(fx)) rotate(fx);//在同一条直线上就进行 zig-zig
else rotate(cur);//否则进行 zig-zag
}
rotate(cur);
fx=fa[cur];
}
root=cur;
}
插入
对于插入操作,我们可以进行以下几种分类讨论:
- 根节点为空:这棵树还没建出来,直接新建一个节点表示根节点即可。
- 不断通过二叉搜索树的性质找到这个点应该插入的位置,直到遇到情况 \(3\) 或者情况 \(4\)。
- 应该插入的位置已经有同种权值的点了:直接让那个点的 \(cnt\) 加一
- 应该插入的位置为空:新建一个点,并维护一下信息,然后把它转到根节点上去。
代码如下:
void ins(int x){
if(!root){
root=++cnt;
tree[cnt].v=x;
tree[cnt].cnt=1;
tree[cnt].son[0]=tree[cnt].son[1]=0;
return;
}
int cur=root,fx=0;
while(1){
if(tree[cur].v==x){
tree[cur].cnt++;
pushup(cur);
pushup(fx);
splay(cur);
break;
}
fx=cur;
cur=tree[cur].son[tree[cur].v<x];
if(!cur){
tree[++cnt].v=x;
tree[cnt].cnt=1;
fa[cnt]=fx;
tree[fx].son[tree[fx].v<x]=cnt;
pushup(cnt);
pushup(fx);
splay(cnt);
break;
}
}
}
删除
对于删除操作,首先我们用 splay 操作把要删的点给旋到根节点上去,然后我们也可以进行以下几种分类讨论:(实际上与上文提到的二叉搜索树的删除操作类似)
- \(cnt\) 不为 \(1\):直接减 \(cnt\)
- 左右儿子都为空:直接删掉
- 左儿子为空,右儿子不为空:把右儿子提上来做新的根节点,然后删掉
- 左儿子不为空,右儿子为空:把左儿子提上来做新的根节点,然后删掉
- 左右儿子皆不为空:找到前驱/后继,把它提上来做新的根节点,然后删掉
代码如下:
void del(int x){
int cur=find(x);//find 函数表示在树里面找与 x 的权值对应的树节点编号
splay(cur);
if(tree[cur].cnt>1){
tree[cur].cnt--;
pushup(cur);
return;
}
if(!tree[cur].son[0]&&!tree[cur].son[1]){
tree[cur].v=tree[cur].cnt=fa[cur]=tree[cur].siz=0;
root=0;
}
else if(tree[cur].son[0]&&!tree[cur].son[1]){
root=tree[cur].son[0];
tree[cur].v=tree[cur].son[0]=tree[cur].cnt=fa[cur]=tree[cur].siz=0;
fa[root]=0;
}
else if(!tree[cur].son[0]&&tree[cur].son[1]){
root=tree[cur].son[1];
tree[cur].v=tree[cur].son[1]=tree[cur].cnt=fa[cur]=tree[cur].siz=0;
fa[root]=0;
}
else{
int now=pre(root);
now=find(now);
fa[tree[cur].son[1]]=now;
tree[now].son[1]=tree[cur].son[1];
tree[cur].v=tree[cur].son[1]=tree[cur].son[0]=tree[cur].cnt=fa[cur]=tree[cur].siz=0;
pushup(now);
}
}
查询某个数的排名
由于不保证查询的数一定出现在该数据结构中,所以我们先把这个数插进来。由于每次操作之后的这个点都会是根节点,再根据二叉搜索树的性质,直接输出它左子树大小加一即可。最后再把这个数给删掉。
int query_rank(int x){
ins(x);
int cur=find(x);
int ansi=tree[tree[cur].son[0]].siz+1;
del(x);
return ansi;
}
查询第 \(k\) 个的数
用二叉搜索树的方式找即可。用循环而不是递归的原因,大抵应该是方便当没有第 \(k\) 个数输出的是 \(0\) 吧。递归也行应该。
int query_kth(int k){
int cur=root;
while(1){
if(tree[tree[cur].son[0]].siz>=k) cur=tree[cur].son[0];
else if(tree[tree[cur].son[0]].siz+tree[cur].cnt>=k) return tree[cur].v;
else{
k=k-tree[tree[cur].son[0]].siz-tree[cur].cnt;
cur=tree[cur].son[1];
}
}
}
前驱和后继
按照二叉搜索树前驱和后继的查询方法,输出左子树里面最靠右的或者右子树里面最靠左的即可。
int pre(int x){
int cur=tree[root].son[0];
if(!cur) return 0;
while(tree[cur].son[1]) cur=tree[cur].son[1];
splay(cur);
return tree[cur].v;
}
int suf(int x){
int cur=tree[root].son[1];
if(!cur) return 0;
while(tree[cur].son[0]) cur=tree[cur].son[0];
splay(cur);
return tree[cur].v;
}
应用
区间操作
splay 很有意思的地方在于比起线段树等数据结构,它能进行一些更复杂的序列操作,比如区间翻转(前面提到的 fhq treap也可以实现)。
由于由序列构成的 splay 的一颗子树代表原序列的一段区间,所以我们考虑把序列操作放到 splay 上,然后将代表 \(a_{l-1}\) 的节点 splay 到跟,代表 \(a_{r+1}\) 的点 splay 到跟的右儿子。此时代表 \(a_{r+1}\) 的树上这个点的左子树就是区间 \([l,r]\)。
对于区间翻转操作,考虑和 fhq treap 进行类似的操作,交换左右儿子并打上标记。
扩展
感觉 splay 更有意思的地方在于它是 Link-Cut Tree(LCT)的基础,这可能也是很多人学 splay 的目的。但我还不会 LCT,所以先咕着。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号