【算法】莫队
一、概念
莫队是一种应用于离线询问的优美暴力算法。它是主要思想是让区间的左端点和右端点移动的距离加起来最短。
二、实现
假设现在有这样一串序列：\(1,1,4,5,1,4\)，我们现在要求询问区间内的 \(1\) 的出现次数。
如果我们现在已经统计到了区间 \((2,3)\)，现在询问 \((1,5)\)。
现在的答案是这样的：
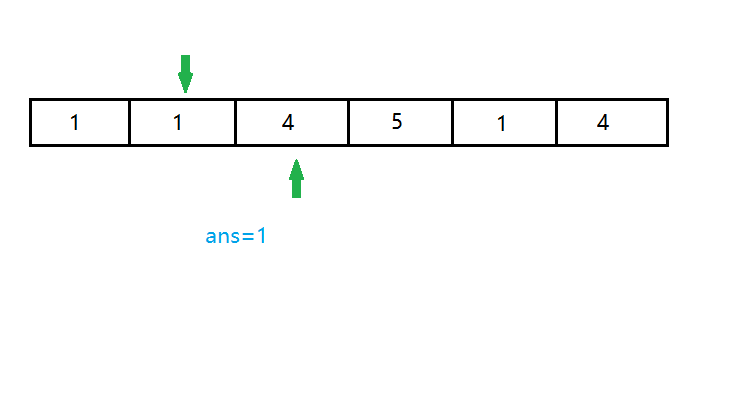
我们发现现在的左端点 \(x=2\) 在询问的左端点的右边，所以我们将当前左端点向左移一位。现在维护的区间 \([1,3]\) 有两个 \(1\) 了。
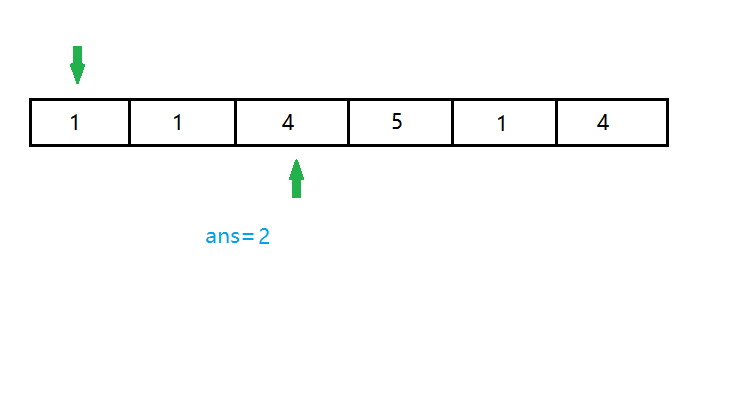
我们又发现现在的右端点 \(y=3\) 在询问的右端点左边，所以我们将当前右端点向右移一位。现在维护的区间 \([1,4]\) 还是有两个 \(1\)。
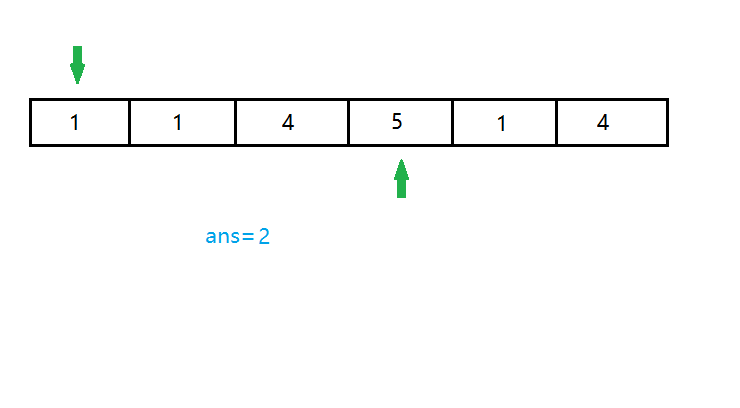
这时候的右端点还是在询问的右端点。所以我们再将右端点向右移一位。现在维护的区间 \([1,5]\) 有三个 \(1\) 了。
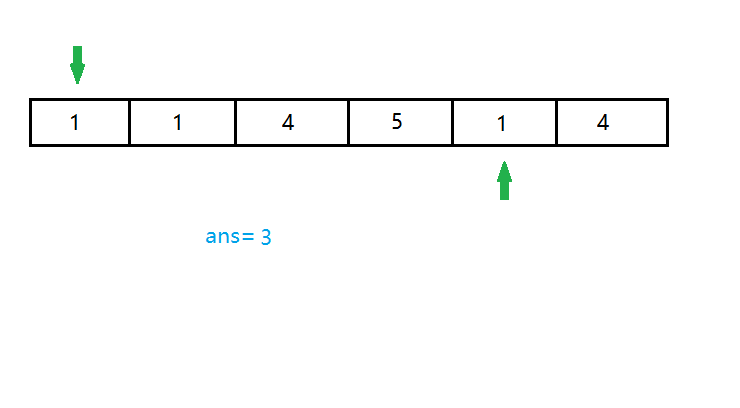
这时候访问到的区间与询问的区间完全一样，我们就可以存储答案了。
这就是莫队的思想了（。你会发现这十分的像暴力，的确如此。但是为了保证时间复杂度，我们要引入分块的思想。先将 \(l\) 按照所在块的编号排序，在每个块中，再按 \(r\) 的大小排序。
这样的话我们发现在每个块中，\(r\) 最多会移 \(n\) 次，每换一次块，就可能多移 \(n\) 次。同时，每次询问 \(l\) 都可能移动 \(size\) 次。所以时间复杂度应该为 \(O(n\times num+m\times size)=O(\frac{n^2}{size}+m\times size)\)。
我们发现每换一次块，\(r\) 可能会从最右边跑到最左边，这显然不优。所以我们考虑奇偶性优化，如果第一个块的编号为偶数，那么块的编号为偶数就将 \(r\) 升序排序，为奇数就将 \(r\) 降序排序。如果第一个块的编号为奇数，那么就都反过来。
三、代码
感觉比较板的题是这题：小B的询问
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e4+5;
int n,m,k;
int a[N];
int buc[N];
int ansi[N];
int T;
int sum;
struct node{
int l,r,id;
}q[N];
bool cmp(node x,node y){
if(x.l/T==y.l/T) return x.r<y.r;
return x.l<y.l;
}
void add(int x){
sum-=buc[a[x]]*buc[a[x]];
buc[a[x]]++;
sum+=buc[a[x]]*buc[a[x]];
}
void del(int x){
sum-=buc[a[x]]*buc[a[x]];
buc[a[x]]--;
sum+=buc[a[x]]*buc[a[x]];
}
signed main(){
ios::sync_with_stdio(false);
cin>>n>>m>>k;
T=sqrt(n);
for(int i=1;i<=n;++i) cin>>a[i];
for(int i=1;i<=m;++i){
cin>>q[i].l>>q[i].r;
q[i].id=i;
}
sort(q+1,q+m+1,cmp);
int x=1,y=0;
for(int i=1;i<=m;++i){
int qx=q[i].l,qy=q[i].r;
while(x>qx){
x--;
add(x);
}
while(y<qy){
y++;
add(y);
}
while(x<qx){
del(x);
x++;
}
while(y>qy){
del(y);
y--;
}
ansi[q[i].id]=sum;
}
for(int i=1;i<=m;++i) cout<<ansi[i]<<"\n";
return 0;
}
四、例题
CF617E
萌新的第一道莫队维护子区间题
异或有些很好的性质。
- 如果 \(a\oplus b=c\)，那么 \(a\oplus c=b\)
- \(a\oplus a=0\)
考虑它维护的是区间异或值，所以可以维护前缀异或值。所以问题相当于 \(sum[r]\oplus sum[l-1]=k\)，交换一下得，\(sum[r]\oplus k=sum[l-1]\)。这样用个桶维护一下 \(sum\) 的出现次数就行。
CF1000F
常规的用桶维护数字的出现次数，如果这个数恰好出现一次就把它放进栈中。输出的时候直接输出栈顶就行，删除的时候可以预先处理它在栈中的位置，然后将它与栈顶交换一下后删除栈顶。
CF877F
又是一道维护子区间的题，所以还是可以用前缀和。前缀和维护的是这一段前缀中第 \(1\) 类问题比第 \(2\) 类多多少。所以问题转化为 \(sum[r]-sum[l-1]=k\)。如果这是右端点，也就是已知 \(sum[r]\)，那么它的贡献就是 \(sum[l-1]=sum[r]-k\) 的次数。如果这是左端点的同理。由于 \(a[i]\) 的数据范围有点大，所以要离散化一下，还要离散化它的贡献点。
Fibonacci-ish II
[HNOI2016] 大数
依旧是维护子区间的题，所以依旧用前缀和。\(sum[i]\) 表示前 \(i\) 个数组成的数对 \(p\) 取模的值，可以这样递推求出 \(sum[i]=(10sum[i-1]+a[i])%p\)。这样一段区间对 \(p\) 取模为 \(0\) 可以写成这样的式子：
\(\because sum[r]-sum[l-1]\times 10^{r-l+1} \equiv 0\pmod p\)
\(\therefore sum[r] \equiv sum[l-1]\times 10^{r-l+1} \pmod p\)
\(\therefore sum[r]\times 10^{-r} \equiv sum[l-1]\times 10^{-(l-1)} \pmod p\) （两边同时乘以 \(10^{-r}\)）
所以我们可以维护一个 \(f[i]\) 表示 \(sum[i]\times 10^{-i}\)。但还需要特判一下 \(p=2\;or\;5\) 的情况，因为此时最后一个式子并不成立，成立的只有 \(sum[r] \equiv sum[l-1]\times 10^{r-l+1} \equiv 0\pmod p\)。
其实这题用后缀和好维护一点，此时的递推式是 \(sum[i]=sum[i+1]+a[i]\times 10^{n-i+1}\)。一段区间对 \(p\) 取模为 \(0\) 写成的式子是这样的：
\(\frac{sum[l]-sum[r+1]}{10^{n-r}} \pmod p\)。如果 \(p=2\;or\;5\) 还是和上面一样特判一下，计算一段区间内有多少个数是以 \(0,2,4,6,8\) 或 \(0,5\) 结尾的即可。否则 \(sum[l]\equiv sum[r+1]\pmod p\)，直接算。
