【算法】基础数据结构
一、单调栈
1. 概念
满足单调性的栈结构,常用于 RMQ 问题。
2. 实现
为满足单调性,我们在栈的基础上额外判断以下栈顶元素是否大于/小于当前元素。以下面的序列 \(1\;7\;4\;3\;2\;8\) 为例,需要求每一个数右边第一个比它大的数。考虑维护单调递减栈,才能保证不会有数没有找到答案便被弹出栈了。
现在将 \(7\) 放入已有 \(1\) 的栈中。
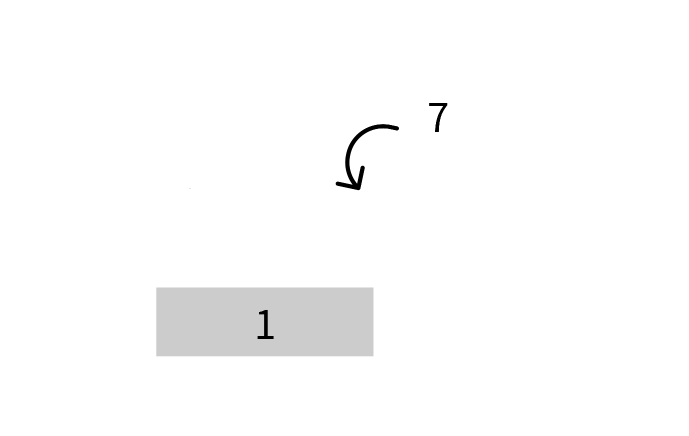
由于这是一个单调递减栈,\(7 > 1\),此时将 \(1\) 弹出,放入 \(7\),并得出 \(1\) 右边第一个大于它的数就是 \(7\)。证明如下:
若当前栈顶为 \(x\),当前元素为 \(y\)。假设序列中存在一个数 \(z>x\) 且 \(z\) 在 \(x\) 和 \(y\) 中间,为满足单调性,要么 \(z\) 还没入栈——这显然不可能,因为在 \(z\) 后面的元素 \(y\) 都已经入栈,要么 \(x\) 被 \(z\) 弹出——那么 \(x\) 就一定不是当前栈顶。所以假设不成立。
然后一次将元素 \(4\;3\;2\) 放入,由于它们都符合单调递减性,所以无需弹出。

最后放入 \(8\) ,先和当前栈顶 \(2\) 比较。
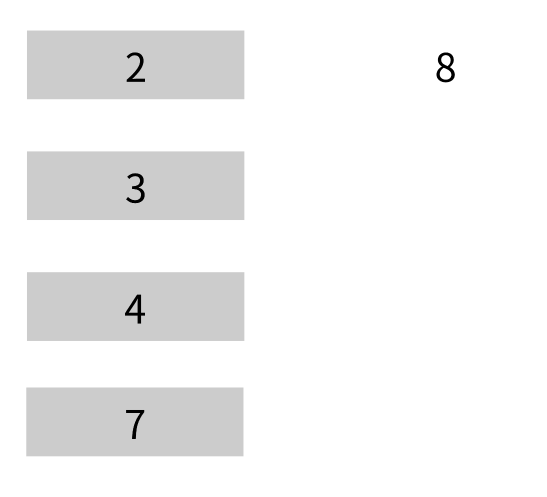
发现 \(8>2\),不符合单调递减性,弹出 \(2\)。再将 \(8\) 和 当前栈顶 \(3\) 比较。
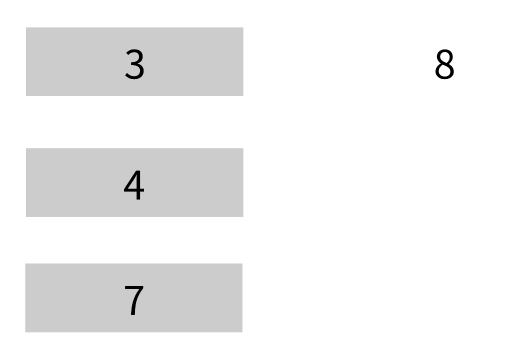
发现 \(8>3\),弹出 \(3\)。以此类推,最后 \(8\) 入栈时,栈里应该什么都没了。
3. 代码
/*
手写栈,stk[]是栈数组,top是栈顶
a[]是原数组,ansi[]存储答案
*/
for(int i=1;i<=n;i++){
while(top!=0&&a[st[top]]<a[i]) ansi[st[top--]]=i;
st[++top]=i;
}
时间复杂度显然 \(O(n)\)
二、单调队列
1. 概念
仿照单调栈的概念有,单调队列是具有单调性的队列。不同于寻常队列的是,这里用到的队列是双端对列。同样用于 RMQ 问题或滑动窗口问题。
2. 实现
为方便描述,这里默认单调队列为单调递减队列。
类似于单调栈。对于滑动窗口问题,由于队列的先进先出性,我们不仅要判断队尾的元素是否大于当前元素,还要判断队首元素是否超过窗口大小限制。
3. 代码
for(int i=1;i<=n;i++){
while(qmin.empty()==false&&qmin.back().w>=a[i]) qmin.pop_back();
while(qmin.empty()==false&&qmin.front().pos<i-k+1) qmin.pop_front();
node now={i,a[i]};
qmin.push_back(now);
mini[i]=qmin.front().w;
}
同样,时间复杂度也同样 \(O(n)\)
4. 习题
emmmmm...挖个坑,保证八号之前绝对填完(吧)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号