【做题笔记】CSP-S 往年试题
题单
本文章正在持续更新……
【2021】 廊桥分配
题面描述
所有飞机分为两类——国内区和国际区,两区廊桥数量互不干扰。每架飞机遵循“先到先得”的原则,优先选择编号最小的廊桥,如果该区的廊桥满了,便前往远机区(假设远机区数量无限)。
求一种分类方案(将廊桥分给国内区和国际区),使得能停靠在廊桥旁飞机的数量最多。
题解
不难想到枚举国内区和国际区各自的数量,然后每次都进行一次模拟,用优先队列维护即可。
这样你可以获得优秀的 45pts,好好卡一下可以卡到 60pts。
然后再思考正解,先观察一下样例解释:
也就是,如果只有 \(x\) 个廊桥的时候第 \(i\) 架飞机可以停在廊桥旁,那么之后所有大于 \(x\) 个廊桥的方案数,第 \(i\) 架飞机都可以被满足。
或者我们只考虑国内区,假设有无限个廊桥(其实有多少架飞机,就多少个廊桥就行),这样每个飞机都可以停靠在一个廊桥边,设 \(sum_{[i]}\) 表示有多少架飞机停在编号为 \(i\) 的廊桥边。现在廊桥数突然减少到了 \(x\) 个,那么原本停靠在编号在 \(x\) 之后的飞机现在一定都没廊桥可以停了。那么现在可以停在廊桥边上飞机的数量,就是 \(\sum\limits_{i=1}^x sum_{[i]}\)。
这样预处理一遍,查询枚举后用前缀和即可。
优先队列时间复杂度是 \(O(\log n)\),总共最多有 \(m_1+m_2\) 次队列操作,故总时间复杂度为 \(O((m_1+m_2)\log n)\)。
代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,gn,gw;
int suma[N],sumb[N];
#define getchar()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
char buf[1<<21],*p1=buf,*p2=buf;
template <typename T>
inline void read(T& r) {
r=0;bool w=0; char ch=getchar();
while(ch<'0'||ch>'9') w=ch=='-'?1:0,ch=getchar();
while(ch>='0'&&ch<='9') r=r*10+(ch^48), ch=getchar();
r=w?-r:r;
}
struct node{
int st,en;
}pn[N],pw[N];
struct Node{
int pos,x;
bool operator < (const Node &a) const{
return this->x>a.x;
}
};
bool cmp(node x,node y){return x.st<y.st;}
int main(){
// freopen("airport3.in","r",stdin);
ios::sync_with_stdio(false);
read(n),read(gn),read(gw);
priority_queue<Node>q,q1;
for(int i=1;i<=gn;i++){
read(pn[i].st),read(pn[i].en);
Node nxt={0,i};
q.push(nxt);
}
//处理国内航班
sort(pn+1,pn+gn+1,cmp);//首先按抵达时间排序
for(int i=1;i<=gn;i++){
while(q1.empty()==false&&q1.top().x<=pn[i].st){//如果飞机飞走了
Node nxt={0,q1.top().pos};
q1.pop();
q.push(nxt);
}
int x=q.top().x;
q.pop();
suma[x]++;
Node nxt={x,pn[i].en};
q1.push(nxt);
}
//清空队列们
while(q.empty()==false) q.pop();
while(q1.empty()==false) q1.pop();
//处理国际航班
for(int i=1;i<=gw;i++){
read(pw[i].st),read(pw[i].en);
Node nxt={0,i};
q.push(nxt);
}
sort(pw+1,pw+gw+1,cmp);
for(int i=1;i<=gw;i++){
while(q1.empty()==false&&q1.top().x<=pw[i].st){
Node nxt={0,q1.top().pos};
q1.pop();
q.push(nxt);
}
int x=q.top().x;
q.pop();
sumb[x]++;
Node nxt={x,pw[i].en};
q1.push(nxt);
}
//处理前缀和
for(int i=1;i<=n;i++) sumb[i]+=sumb[i-1];
for(int i=1;i<=n;i++) suma[i]+=suma[i-1];
//枚举答案
int maxi=0;
for(int x=0;x<=n;x++){
int y=n-x;
maxi=max(suma[x]+sumb[y],maxi);
}
cout<<maxi;
return 0;
}
【2021】 括号序列
题面描述
给出一个长度为 \(n\) 的序列,其中有一些位置的字符已经确定,另外一些位置的字符尚未确定(用 ? 表示),询问有多少种将所有尚未确定的字确定的方法,使得得到的字符串是一个符合规范的序列?
如果一个序列符合规范,则它需要满足以下条件:
()、(S)均是符合规范的超级括号序列,其中S表示任意一个仅由不超过 \(\bm{k}\) 个字符*组成的非空字符串(以下两条规则中的S均为此含义);- 如果字符串
A和B均为符合规范的超级括号序列,那么字符串AB、ASB均为符合规范的超级括号序列,其中AB表示把字符串A和字符串B拼接在一起形成的字符串; - 如果字符串
A为符合规范的超级括号序列,那么字符串(A)、(SA)、(AS)均为符合规范的超级括号序列。 - 所有符合规范的超级括号序列均可通过上述 3 条规则得到。
题解
观察序列的情况,整理可得有以下几种情况:
- 序列左右两边都是
*,如********或***()***。 - 序列一边是
*,一边是(),如(**)***或**(****)。 - 序列左右两边都是
(),如(**)*(***)或(**(**)**(***))。
不难发现,只有第三种情况符合条件,而第三种情况细分可以得到以下几种情况:
(******),由第一种情况加上括号得到。(***)(*)或(***)**(*),由第三种情况和第二种情况中*在左边得到。(***(*)),由第二种情况加上括号得到。
这样这三种情况显然不够用,我们需要再加几种情况判断。新得到的情况由以下几种:
- 全部都是
* - 左右两个括号相匹配,包含里面所有字符。
- 左边是
*,右边是括号序列。 - 左右两边都是括号,特殊地,第一种情况也包含在内。
- 左边是括号序列,右边是
*。 - 左右两边都是
*,特殊地,第零种情况也包含在内。
于是我们可以设计一个三维状态 \(dp_{[i][j][6]}\)。
\(dp_{[i][j][0]}\):直接特判。
\(dp_{[i][j][1]}=\begin{cases} 0 & i,j\text{ 括号不匹配}\\ dp_{[i+1][j-1][0]+dp[i+1][j-1][2]+dp[i+1][j-1][3]+dp[i+1][j-1][4]} & i,j\text{ 括号匹配} \end{cases}\)
注:没有情况 5 是因为两边都是
*且包含括号序列的是不能在左右两边加上括号的。
\(dp_{[i][j][2]}=\sum\limits_{k=i}^{j-1}(dp_{[i][k][2]}+dp_{[i][k][5]})\times dp_{[k+1][j][1]}\)
注:这里也就是要求左边以
*开头且结尾不限,右边以括号结尾。
\(dp_{[i][j][3]}=\sum\limits_{k=i}^{j-1}(dp_{[i][k][3]}+dp_{[i][k][4]})\times dp_{[k+1][j][1]}+dp_{[i][j][1]}\)
注:这里要求左边以括号开头且结尾不限,右边以全
*序列结尾。
\(dp_{[i][j][4]}=\sum\limits_{k=i}^{j-1}dp_{[i][k][3]}\times dp_{[k+1][j][0]}\)
注:这里要求左边以括号开头且结尾也是括号,右边以全
*序列 结尾。
\(dp_{[i][j][5]}=\sum\limits_{k=i}^{j-1}(dp_{[i][k][2]} \times dp_{[k+1][j][0]})+dp_{[i][j][0]}\)
注:这里要求左边以
*开头且结尾为括号,右边以全*结尾。
初始状态: \(dp[i][i-1][0]=1\)
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e2+5;
const int mod=1e9+7;
int n,k;
int a[N];
int dp[N][N][10];
signed main(){
ios::sync_with_stdio(false);
cin>>n>>k;
for(int i=1;i<=n;i++){
char c;
cin>>c;
if(c=='(') a[i]=-1;
else if(c=='*') a[i]=0;
else if(c==')') a[i]=1;
else a[i]=2;
dp[i][i-1][0]=1;
}
for(int len=1;len<=n;len++){
for(int i=1;i+len-1<=n;i++){
int j=i+len-1;
if(len<=k){
if(a[j]==0||a[j]==2) dp[i][j][0]=dp[i][j-1][0];
}
if(len>=2){
if((a[i]==-1||a[i]==2)&&(a[j]==1||a[j]==2)) dp[i][j][1]=(dp[i+1][j-1][0]+dp[i+1][j-1][2]+dp[i+1][j-1][3]+dp[i+1][j-1][4])%mod;
for(int k=i;k<j;k++){
dp[i][j][2]=(dp[i][j][2]+(dp[i][k][2]+dp[i][k][5])*dp[k+1][j][1])%mod;
dp[i][j][3]=(dp[i][j][3]+(dp[i][k][4]+dp[i][k][3])*dp[k+1][j][1])%mod;
dp[i][j][4]=(dp[i][j][4]+dp[i][k][3]*dp[k+1][j][0])%mod;
dp[i][j][5]=(dp[i][j][5]+dp[i][k][2]*dp[k+1][j][0])%mod;
}
}
dp[i][j][3]=(dp[i][j][3]+dp[i][j][1])%mod;
dp[i][j][5]=(dp[i][j][5]+dp[i][j][0])%mod;
}
}
cout<<dp[1][n][3];
return 0;
}
【2021】 回文
题面描述
给定序列 \(a_1, a_2, \ldots, a_{2n}\),在这 \(2n\) 个数中,\(1, 2, \ldots, n\) 分别各出现恰好 \(2\) 次。进行 \(2 n\) 次操作,创建一个长度为 \(2n\) 序列 \(b\),使得 \(b\) 是一个回文数列,判断是否可行,如果可行便输出字典序最小的方案。操作如下:
- 将序列 \(a\) 的开头元素加到 \(b\) 的末尾,并从 \(a\) 中移除。
- 将序列 \(a\) 的末尾元素加到 \(b\) 的末尾,并从 \(a\) 中移除。
题解
\(\tiny\text{据说这题竟比T2水}\)。
显然可以贪心的选择 L,如果不行再选择 R,于是可以得到一个 \(40pts\) 的暴力。
至于正解,我们可以先分类讨论第一次怎样取,这里只解说左边的情况。
这样 \(b_{[1]}=a_{[1]}\),那么假设 \(a\) 数组中 \(a_{[x]}=a_{[1]}\) 的话,\(b_{[2n]}=a_{x}\)。也就是 \(a_{[x]}\)一定是 \(a\) 数组中最后一个取出的元素。
那么无论你是怎样取的,\(a_{[x-1]}\) 肯定是比 \(a_{[1]},a_{[2]}...a_{[x-2]}\) 更晚被取到的。同理,\(a_{[x+1]}\) 也会比 \(a_{[x+2]},a_{[x+3]}...a_{[n]}\) 更晚取到。
稍微解释一下,由于 \(a_{[x]}\) 在其他元素被取完时一定是固定不动的,所以它可以将整个序列分为两部分,左半部分是不能从右边取的(因为 \(a_{[x]}\) 还在那呢),同理右半部分也不能从左边取。这样整个序列就被分成了两个栈。
借助图片,我们分析具体的实现:
(此时 \(n=5,A_{[1]}=A_{[6]}\),定义 \(ansi[i]\) 为第 \(i\) 次操作的情况)
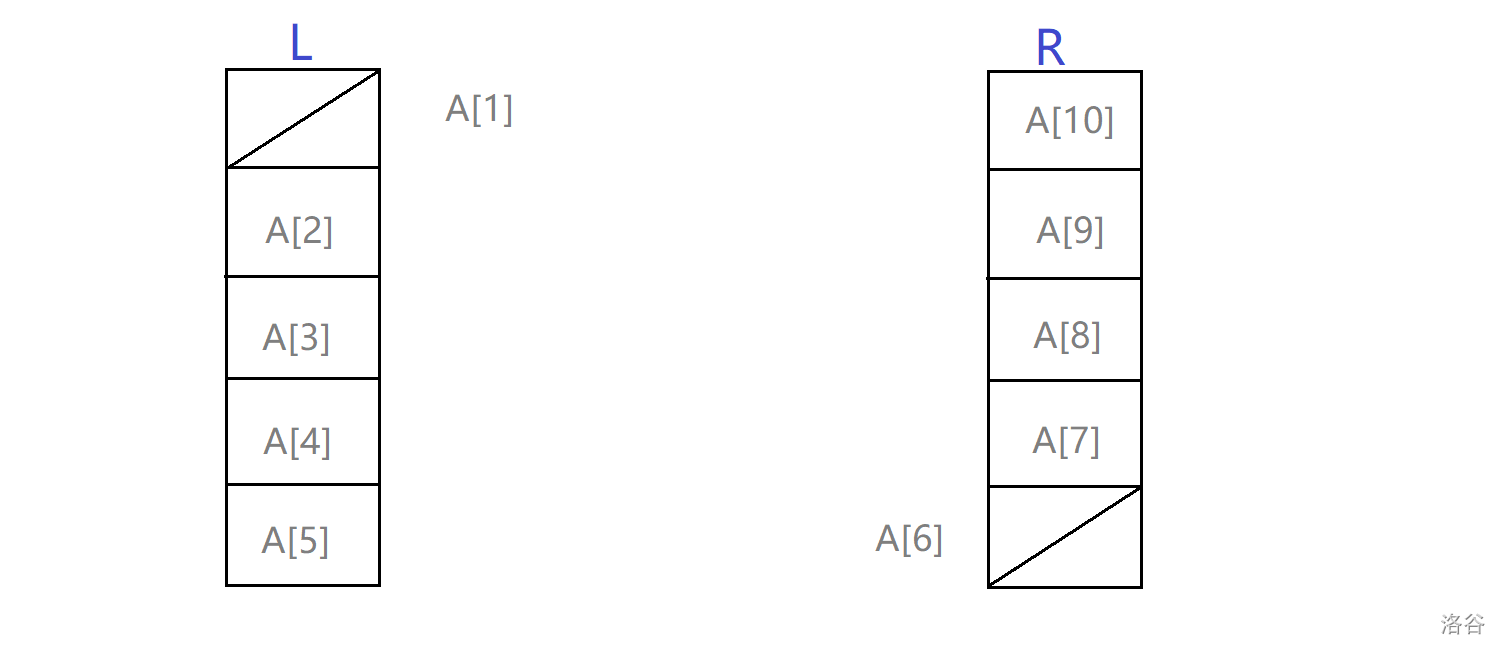
这时候如果拿出 \(A_{[2]}\),现在的情况可以分为三种情况:
-
如果 \(A_{[7]}=A_{[2]}\) 的话,代表第 \(9\) 次操作一定是取出 \(A_{[7]}\),于是 \(ansi_{[2]}=L,ansi_{[9]}=R\)。
-
如果 \(A_{[5]}=A_{[2]}\) 的话,代表第 \(9\) 次操作一定是取出 \(A_{[5]}\),于是 \(ansi_{[2]}=L,ansi_{[9]}=L\)。
-
除上面两种情况外,由于与 \(A_{[2]}\) 相等的数 \(x\) 不在栈底,但第 \(9\) 次操作又不得不是取出 \(x\),那么在 \(x\) 下面的数就一定不能被取出。那么这种情况无解。
再分类讨论拿出右边的情况就可以过了这道题了。
代码
暴力:
点击查看代码
void dfs(int x){//x代表已经填了多少位
if(x==n*2+1){
fin=true;
for(int i=1;i<=n*2;i++){
if(ansi[i]==1) cout<<"L";
else cout<<"R";
}
return;
}
if(x<=n||a[lt]==b[n*2-x+1]){
ansi[x]=1;
b[x]=a[lt++];
dfs(x+1);
lt--;
if(fin==true) return;
}
if(x<=n||a[rt]==b[n*2-x+1]){
ansi[x]=2;
b[x]=a[rt--];
dfs(x+1);
rt++;
}
}
正解:
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int n,a[N];
int ansi[N];//存贮操作的答案,1是L,2是R
deque<int>lt,rt;//虽然分析中是栈,但由于还要弹出栈底元素,故用双端队列更好
void start(){//初始化
lt.clear();
rt.clear();
memset(ansi,0,sizeof(ansi));
}
int fin(int l,int r,int x){//找到与x相等的数
for(int i=l;i<=r;i++) if(a[i]==x) return i;
return -1;
}
void solve(){
int x=2;
while(lt.empty()==false||rt.empty()==false){//如果还有数
if(rt.empty()==true){//右边的取空了,就只考虑左边的了。下面同理
if(lt.front()!=lt.back()){
ansi[1]=0;
return;
}
ansi[x]=ansi[2*n-x+1]=1;
lt.pop_front();
lt.pop_back();
}
else if(lt.empty()==true){
if(rt.front()!=rt.back()){
ansi[1]=0;
return;
}
ansi[x]=ansi[2*n-x+1]=2;
rt.pop_front();
rt.pop_back();
}
else{//对应四种分类讨论情况
if(lt.size()>=2&<.front()==lt.back()){//这里一定要保证至少还有两个数,要不然就是自己与自己相等了
ansi[x]=ansi[2*n-x+1]=1;
lt.pop_front();
lt.pop_back();
}
else if(lt.front()==rt.back()){
ansi[x]=1,ansi[2*n-x+1]=2;
lt.pop_front();
rt.pop_back();
}
else if(rt.size()>=2&&rt.front()==rt.back()){
ansi[x]=ansi[2*n-x+1]=2;
rt.pop_front();
rt.pop_back();
}
else if(lt.back()==rt.front()){
ansi[x]=2,ansi[2*n-x+1]=1;
rt.pop_front();
lt.pop_back();
}
else{
ansi[1]=0;
return;
}
}
x++;
}
}
int main(){
ios::sync_with_stdio(false);
int t;
cin>>t;
while(t--){
cin>>n;
start();
for(int i=1;i<=n*2;i++) cin>>a[i];
//取L
int pos=fin(2,n*2,a[1]);
ansi[1]=ansi[2*n]=1;
for(int i=2;i<=pos-1;i++) lt.push_back(a[i]);
for(int i=n*2;i>=pos+1;i--) rt.push_back(a[i]);
solve();
if(ansi[1]!=0){//如果第一次取L有解,那么它一定是最优解
for(int i=1;i<=n*2;i++){
if(ansi[i]==1) cout<<"L";
else cout<<"R";
}
cout<<"\n";
continue;
}
//取R
lt.clear();rt.clear();
pos=fin(1,n*2-1,a[n*2]);
ansi[1]=2,ansi[2*n]=1;
for(int i=1;i<=pos-1;i++) lt.push_back(a[i]);
for(int i=n*2-1;i>=pos+1;i--) rt.push_back(a[i]);
solve();
if(ansi[1]==0) cout<<"-1\n";
else{
for(int i=1;i<=n*2;i++){
if(ansi[i]==1) cout<<"L";
else cout<<"R";
}
cout<<"\n";
continue;
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号