【算法】浅学 LCA
参考资料
一、概念
最近公共祖先称为 LCA (Lowest Common Ancestor)
它指的是在一颗树中,离两个节点最近的公共祖先
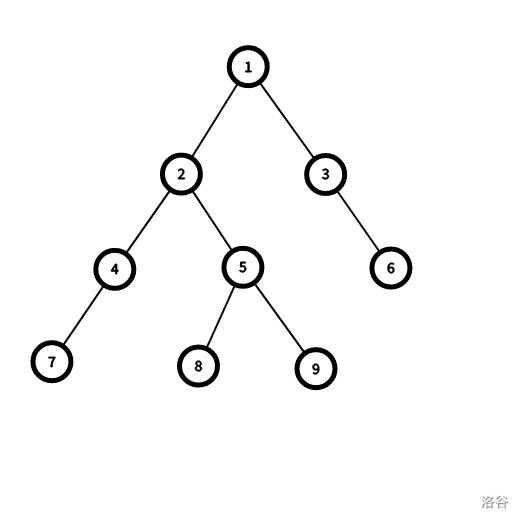
如下图,
节点 7 和节点 5 的最近公共祖先是 2
节点 8 和节点 3 的最近公共祖先是 1
节点 4 和节点 2 的最近公共祖先是 2
那么求 LCA 有哪些方法呢?
二、实现
• 暴力
我们不难想到一种很暴力的想法
如上图,现在我们要求 7 和 5 的 LCA
令 x = 7 , y = 5
首先我们先让 x 和 y 两个节点在同一层,如果深度不一的话,浅的那个节点很有可能就会超过他们的 LCA
x 变为它的父节点,通俗点说就是跳到它父节点的位置
现在 x 和 y 深度相等了,就一起跳到它们各自的父节点,直到 x 和 y 跳到了同一个节点。而这个节点就是它们的 LCA
很显然,时间爆掉了,我们需要一点优化
• 倍增
上面的想法一格一格地跳太慢了,那么可不可以让它们一次跳一大块呢?
这里我们就可以运用倍增思想,不了解倍增思想的可以先看看参考资料那
先定义几个数组
\(fa_{[i][j]}\) 表示 i 节点的第 \(2^j\) 个祖先
\(deep_{[i]}\) 表示 i 节点的深度
首先还是一样的,将 x 和 y 跳到同一深度,这里也要用倍增法
每次考虑跳 \(2^n\) 次,但是不能超过 LCA 的深度
也就是每次跳的时候,判定一下如果跳了 \(2^n\) 后,两个节点的父亲会不会相同,如果相同,就表示跳到 LCA 或者跳过头了
最后输出跳完之后 x 和 y 的父节点即可
预处理 fa 数组时,我们可以运用一个显而易见的结论,i 的 \(2^j\) 个祖先 = i 的 \(2^{j-1}\) 个祖先的 \(2^{j-1}\) 个祖先
表示出来就是这样的:
为什么呢?
首先不难得出,\(2^{j-1}=2^j\div2\) (初中的幂运算)
这在树上可以表现为将 i 上面的 \(2^j\) 层平均分成了两份,跳了一半,再跳一半,当然就可以跳到层的最顶端了
三、代码
• 暴力
• 倍增
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5;
int n,m,s;
int tot,head[N<<1];
int ln,fa[N][35],deep[N];
struct node{
int nex,to;
}edge[N<<1];
void add(int x,int y){
edge[++tot].to=y;
edge[tot].nex=head[x];
head[x]=tot;
}
void dfs(int x,int fx){
fa[x][0]=fx;
deep[x]=deep[fx]+1;
for(int i=1;i<=ln;i++){
fa[x][i]=fa[fa[x][i-1]][i-1];
}
for(int i=head[x];i;i=edge[i].nex){
if(edge[i].to==fx) continue;
dfs(edge[i].to,x);
}
}
int lca(int x,int y){
if(deep[x]>deep[y]) swap(x,y);
for(int i=ln;i>=0;i--){
if((deep[y]-deep[x])>>i&1!=0) y=fa[y][i];
}
if(x==y) return x;
for(int i=ln;i>=0;i--){
if(fa[x][i]!=fa[y][i]){
x=fa[x][i];y=fa[y][i];
}
}
return fa[x][0];
}
int main(){
ios::sync_with_stdio(false);
cin>>n>>m>>s;
ln=log2(n);
for(int i=1;i<=n-1;i++){
int x,y;
cin>>x>>y;
add(x,y);add(y,x);
}
dfs(s,0);
for(int i=1;i<=m;i++){
int x,y;
cin>>x>>y;
cout<<lca(x,y)<<"\n";
}
return 0;
}
四、时间复杂度
• 暴力
| 操作 | 时间复杂度 |
|---|---|
| 预处理 | O(n) |
| 查询 | O(n) |
| 随机树查询 | O(log n) |
• 倍增
| 操作 | 时间复杂度 |
|---|---|
| 预处理 | O(n log n) |
| 查询 | O(log n) |
五、例题
• 斐波那契
problem
Solve
看到题面,一眼 LCA
但这颗树和普通的树不一样,关键在于它编码之间的父子关系,所以我们不妨先观察一下这颗树:

看一下父子节点之间的差值(以 1 和它的孩子们为例)
| 孩子 | 差值 |
|---|---|
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 6 | 5 |
| 9 | 8 |
如果还是没能看出规律的话,不妨在最前面加一个 1,数列就变成了 1 1 2 3 5 8,这就是斐波那契数列
于是我们可以通过这个关系来找到子节点的父亲,与 LCA 的算法思想一样,假设现在要求 x 和 y 两个节点的 LCA
如果 x = y,就意味着它们已经找到了最近公告祖先,直接跳出循环
否则找到 x,y中编号更大的一个,跳到它的父节点
Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=3e5+50;
const int M=60;
int fli[N];
inline int lca(int x,int y){
while(x!=y){
if(x<y) swap(x,y);
int l=0,r=M+1;
while(l+1<r){
int mid=(l+r)>>1;
if(fli[mid]<x) l=mid;
else r=mid;
}
x-=fli[l];
}
return x;
}
signed main(){
ios::sync_with_stdio(false);
int t;
cin>>t;
fli[1]=fli[2]=1;
for(int i=3;i<=M;i++) fli[i]=fli[i-1]+fli[i-2];
while(t--){
int x,y;
cin>>x>>y;
cout<<lca(x,y)<<"\n";
}
return 0;
}
• 紧急集合
Problem
Solve
三个节点的最近公共祖先问题,可能会想到两两求最近公共祖先的想法,但其实这样路径并不会最小,比如下面这图,要求的三个点分别为5 7 8:
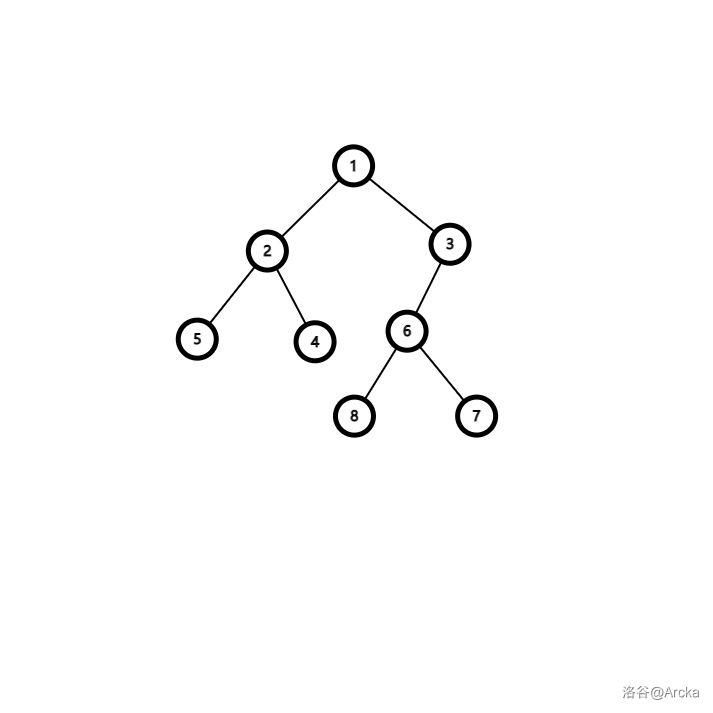
按照之前的思路,它们应该在 1 集合,此时的花费是 8。但如果在 6 集合的话,花费只有 6,明显更优
我们分别对三个点取 LCA,此时:
| 节点 A | 节点 B | LCA |
|---|---|---|
| 5 | 8 | 1 |
| 5 | 7 | 1 |
| 7 | 8 | 6 |
此时有两个 LCA 重合,而更优的是取不重合的那个节点,我们就可以就此写出代码了
Code
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5;
int n,ln;
int tot,head[N<<1];
int deep[N],fa[N][35];
int ansi,money;
struct node{
int to,nxt;
}edge[N<<1];
void add(int x,int y){
edge[++tot].to=y;
edge[tot].nxt=head[x];
head[x]=tot;
}
void dfs(int x,int fx){
deep[x]=deep[fx]+1;
fa[x][0]=fx;
for(int i=1;i<=ln;i++) fa[x][i]=fa[fa[x][i-1]][i-1];
for(int i=head[x];i;i=edge[i].nxt){
int son=edge[i].to;
if(son==fx) continue;
dfs(son,x);
}
}
int lca(int x,int y){
if(deep[x]<deep[y]) swap(x,y);
for(int i=ln;i>=0;i--){
if(((deep[x]-deep[y])>>i&1)!=0){
x=fa[x][i];
// money+=(1>>i);
}
}
if(x==y) return x;
for(int i=ln;i>=0;i--){
if(fa[x][i]!=fa[y][i]){
x=fa[x][i];y=fa[y][i];
// money+=(1<<i);
}
}
// money++;
return fa[x][0];
}
int main(){
ios::sync_with_stdio(false);
int t;
cin>>n>>t;
ln=log2(n);
for(int i=1;i<n;i++){
int x,y;
cin>>x>>y;
add(x,y);add(y,x);
}
dfs(1,0);
while(t--){
//money=0;
int x,y,z,a,b,c;
cin>>x>>y>>z;
// cout<<lca(lca(x,y),lca(y,z))<<" "<<money<<"\n";
a=lca(x,y),b=lca(y,z),c=lca(x,z);
if(a==b) ansi=c;
else if(b==c) ansi=a;
else ansi=b;
money=deep[x]+deep[y]+deep[z]-deep[a]-deep[b]-deep[c];
cout<<ansi<<" "<<money<<"\n";
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号