【算法】线段树
推荐博客
【算法】线段树学习笔记(膜拜 yzy!)
线段树学习笔记(入门) (膜拜 slcloud!)
一、概念
线段树本质上是一颗二叉树,用于处理区间加法,比如区间和,区间最值等。
它一般定义为父节点的权值等于左孩子结点的权值+右孩子结点的权值,翻译过来就是 \(tree_{[cur]}=tree_{[cur\times2]}+tree_{[cur\times2+1]}\)
(根据树的性质,如果父节点的编号为 i,那么左孩子编号为 \(2\times i\) ,右孩子为\(2\times i+1\))
当然你也可以用位运算来优化,也就是\(tree_{[cur]}=tree_{[cur<<1]}+tree_{[cur<<1|1]}\)
下面这张丑陋的图维护的是区间和:
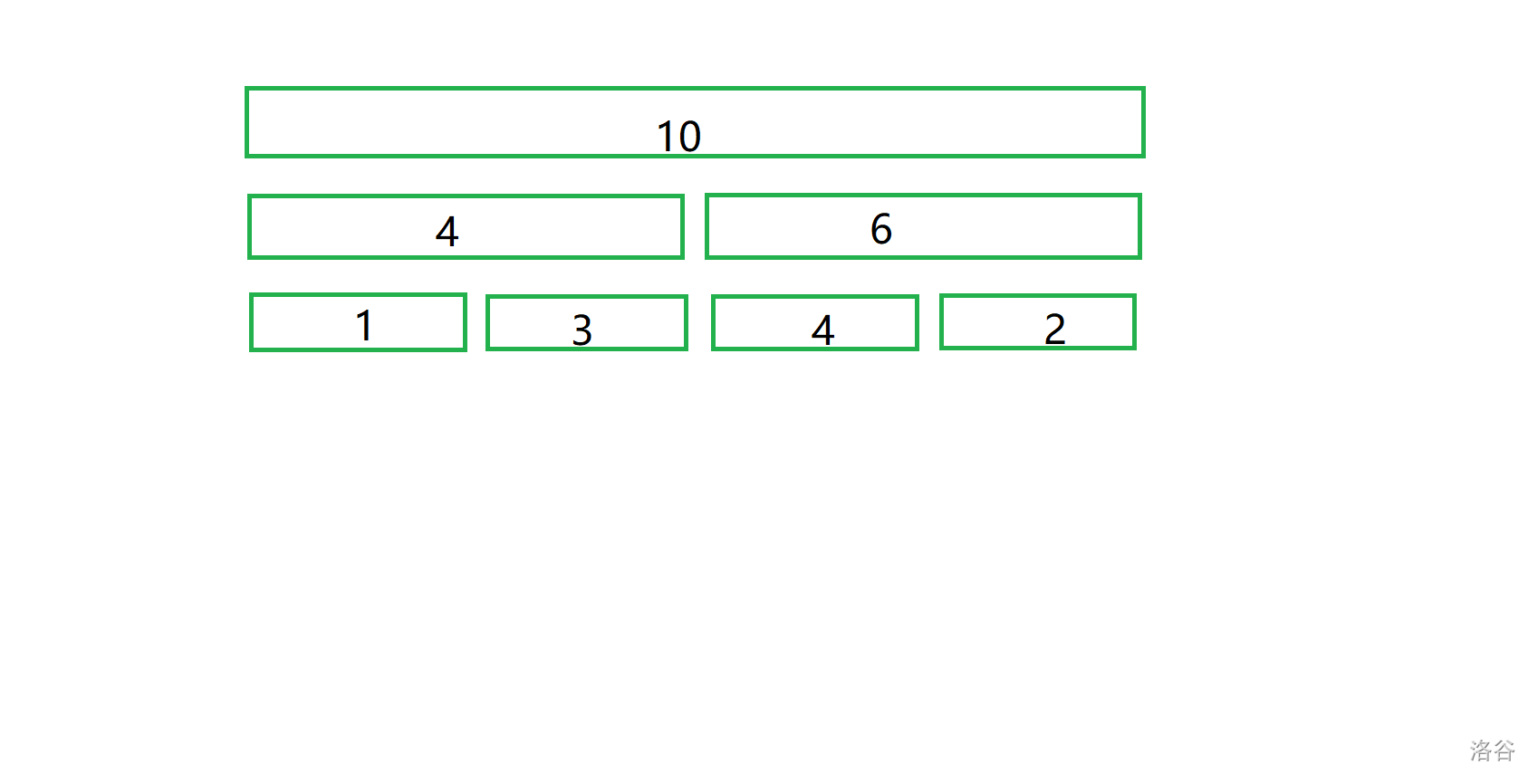
那么问题来了,线段树有什么用呢?
一般来说,线段树在 OI 里面扮演的都是降低时间复杂度工具的角色,常见但不限于,DP优化。
所以当你发现你超时了并且代码中有类似于区间维护之类的部分,就可以考虑线段树优化了!
二、实现
\(\tiny\text{跳的应该没有很快吧awa}\)
• 一些奇怪的废话(可以选择跳过)
假如你现在要吃苹果,你会怎么办?
啊,对!你会先种一颗苹果树,也就是建树。
\(\tiny\text{【冷知识:苹果超市有卖】}\)
这个过程如果用代码实现是这样的:
void build(int cur,int lt,int rt){
if(lt==rt){//当左边界点与右边界点相等时,表示这个点是叶子节点
tree[cur]=a[lt];return;//叶子节点的权值就等于它自己本身
}
int mid=(lt+rt)>>1;
build(cur<<1,lt,mid);//访问左孩子节点
build(cur<<1|1,mid+1,rt);//访问右孩子节点
pushup(cur);//将孩子的信息合并到父节点上
}
而其中的pushup一般因题目而异,这里给出区间和的例子:
void pushup(int cur){
tree[cur]=tree[cur<<1]+tree[cur<<1|1];
}
等你好不容易种完了树,忽然, 树神 Biuld 说它长出来的一个苹果坏了。但是树是没有手的,所以他只能告诉你,请你帮忙去摘。
你到了苹果树旁,经过你的精心照料,这颗苹果树长的异常规整,每条树枝有且仅有两条分叉,但是每次你都可以询问 树神 苹果是在左边还是右边。
于是乎,我们又可以写出这样一段代码:
int query(int cur,int lt,int rt,int qx,int qy){//cur是当前查询节点的编号,lt和rt是当前访问到的区间,qx和qy是要查询的区间
if(lt>qy||rt<qx) return 0;//这里的含义可以见update函数
if(lt>=qx&&rt<=qy){
return tree[cur];
}
pushdown(cur,lt,rt);//查询前先更新
int mid=(lt+rt)>>1;
return query(cur<<1,lt,mid,qx,qy)+query(cur<<1|1,mid+1,rt,qx,qy);
}
你正准备把坏了的苹果给摘下来扔掉。忽然,它学会了魔法!它每次会悄悄告诉你它准备把哪一片苹果全部变成坏的,为了做好摘苹果的准备,你需要更新每段区间内都有多少个坏掉的苹果。
其实就是一个基础的询问区间和代码了!把没坏掉的苹果设为0,坏掉的苹果设为1,这样区间和就是区间内坏掉苹果的数量了。
void update(int cur,int lt,int rt,int qx,int qy,int val){
if(lt>qy||rt<qx) return;//如果跟现在访问到的区间根本没关系
if(lt>=qx&&rt<=qy){//如果好巧不巧的现在访问的区间都在要更新的区间内
addtag(cur,lt,rt,val);return;//啊这里是懒标记,一个优化,等会再讲
}
pushdown(cur,lt,rt);//先把现在的更新了再说
int mid=(lt+rt)>>1;
update(cur<<1,lt,mid,qx,qy,val);//访问左孩子
update(cur<<1|1,mid+1,rt,qx,qy,val);//访问右孩子
pushup(cur);//更新信息
}
但是,作为世界上也许是第一个会魔法的苹果,它十分的烦人,它可能会一直告诉你它刚刚把哪一块地方全部变成了坏苹果,可是又缠着你,不让你去找,浪费你更新区间信息的时间。
这时候,毒瘤出题人路过,跟苹果学会了这一招,于是为了防止不超时,有一种很简单的优化方式,也就是懒标记
它的大概思路是这样的:每当要更新一段区间的信息时,它并不直接更改整个区间,而是在父节点上存储要更改的内容,当询问到这个区间时,再将所有有关这个区间更新的内容随着访问一起传给孩子节点。
比如这样:
现在你正在和 yzy 玩一个游戏,yzy 会告诉你一个序列,每次她可能会将序列 x 到 y 的所有数全部加上 val ,或者询问你 x 到 y 的区间和。
现在她给你了这样一个序列:1 8 1 4 0 8 2 4
我们先按照这个序列建一颗树

第一次操作:yzy 决定将 1 到 4 这个区间内所有数全部加上 2
于是,用懒标记优化的树应该是这样:
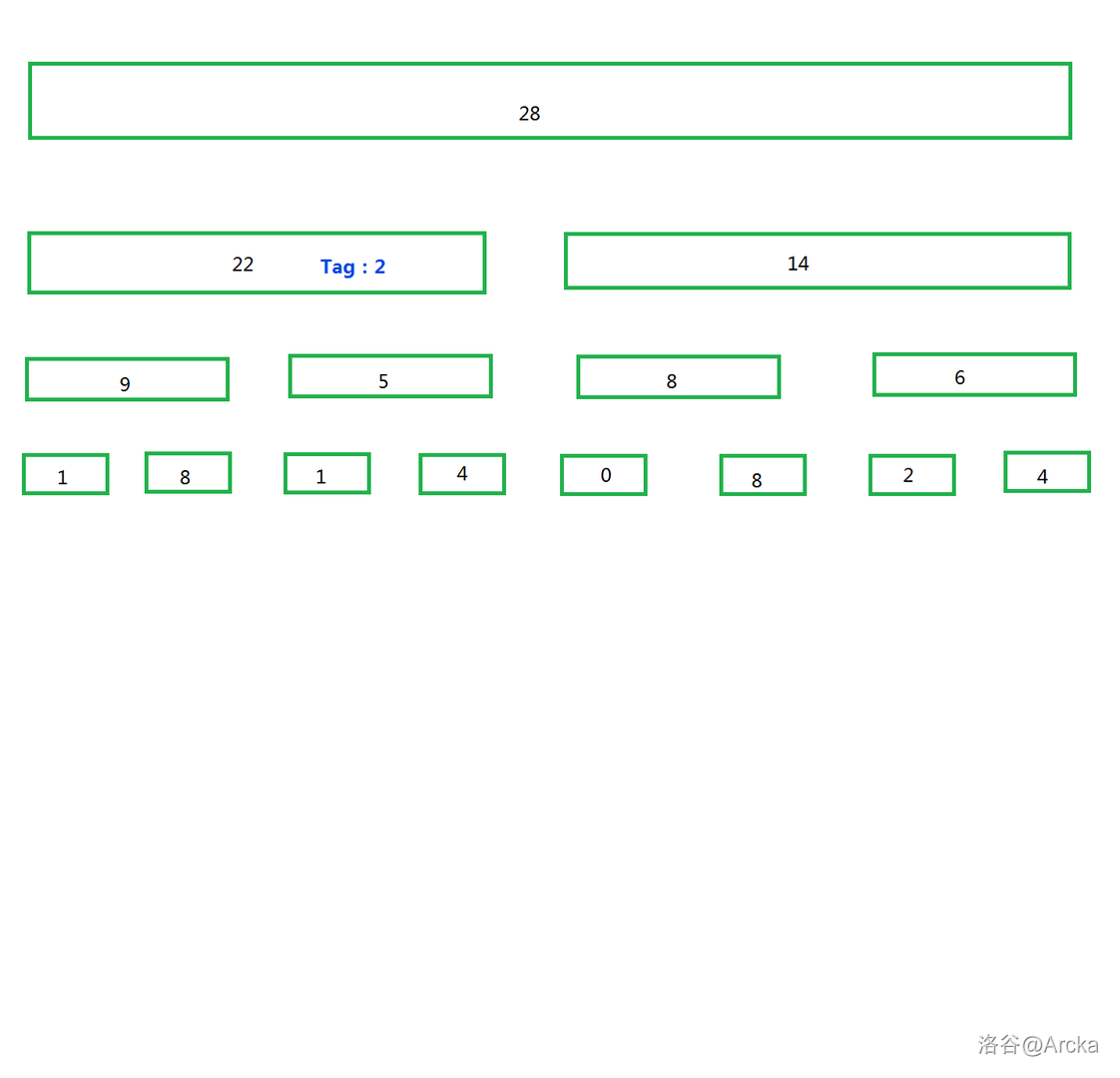
也就是说,找到一个完全包含更新区间的区间,首先要更新它自己本身的值,然后打上标记。
那么,为什么要更新自己本身的值呢**
我们要明确,打上标记的含义是修改了叶子节点。 所以当目前节点不是叶子结点时,标记的数并不符合这个区间的值,如果等更新了叶子结点后再更新父节点,那么时间复杂度依然会很高
第二次操作:yzy 决定将 4 到 5 这个区间内所有数全部加上 1
然后我们维护的树会变成这样:
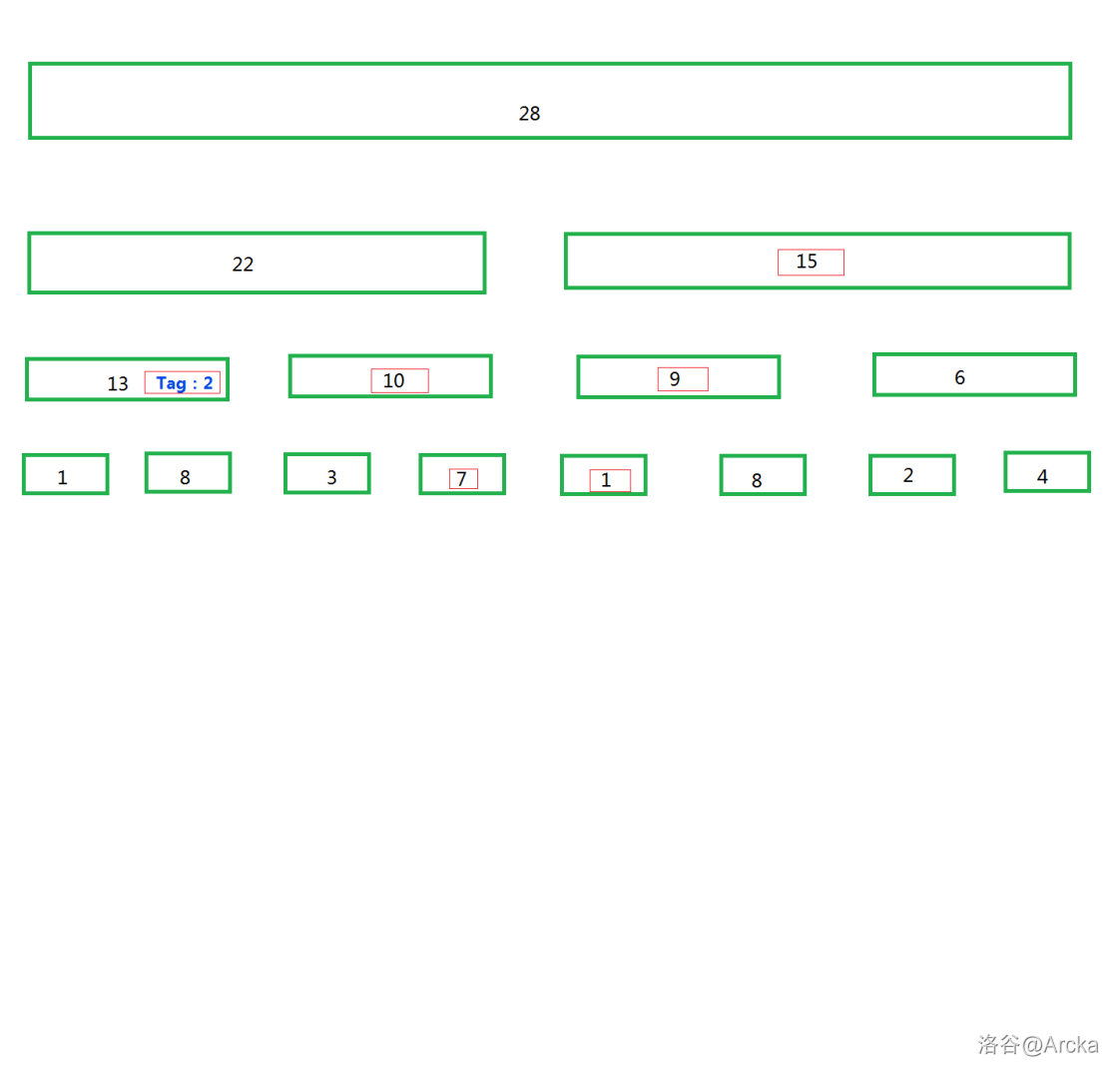
\(\tiny\text{【图丑见谅QAQ】}\)
这次操作和上次操作又有不一样了,我们访问到了上一次打过标记的节点,因为这一次这个节点并不完全包含要更新的区间,所以我们继续往下找
往下找的时候要顺带着将标记下传,以更新它的两个孩子节点,直到访问到 4 这个区间。右边的更新也是一样的道理
第三次操作:yzy 想要知道 1 3 这个区间的和
\(\tiny\text{【懒得画图了】}\)
事实上这时候我们也不要把那唯一的标记下传,就变成了一个基础的访问区间和的操作
• 总体思路
以区间和为例
1. 建树
对于每一个叶子节点,我们直接原数组赋值给它就行;对于每一个非叶子节点,它的值就是它左孩子和右孩子节点的和。
也就是,先访问父节点但从叶子节点开始更新值,最后统计到父节点中。
2. 更新
假设我们现在访问到了区间 L ,需要更新的区间是 Q,我们可以对 L 进行分类讨论:
如果 L 与 Q 没有任何重合的地方,直接不访问 L 区间,返回;
如果 Q 包含 L ,直接更新 L 整个区间;
否则,就访问 L 区间的左右区间,代码表现为访问左右孩子节点,最后统计到整个 L 区间即可
3. 询问
和更新类似
• 懒标记
懒标记是线段树一种常用的优化,就算没有一直询问没让你更新的数据点,它也能大大减小你的时间复杂度
现在我们依旧假设访问到了区间 L,需要更新的区间是 Q,那么当 Q 包含 L 时,我们考虑不直接更新 L,而是给 L 打上一个标记,等到之后访问到 L 区间时,我们再使用
• 注意事项
1. 使用线段树之前注意建树,也就是调用 build 函数
不要小看这一点,很多一开始接触线段树的人,甚至是接触到有一段时间的人,都会忘记建树。包括但不限于我,机房的一些神犇
2. 使用线段树时,tree 数组要开四倍空间
这也是大部分人 RE 的原因,你可以自己画一个图试试为什么要开四倍空间
3. 使用线段树时,tag 数组也要开四倍空间
这是这个蒟蒻刚刚打线段树 RE 的原因,所以在此建议在不 MLE 的前提下,数组开 10 倍空间
4. pushdown 的顺序
pushdown 的顺序尤其要注意,否则可能会浪费你几个小时的时间。一般来说,在正常的线段树操作下,先进行乘法的 pushdown,再进行加法的 pushdown 。其余操作因题目而异
5. 关于函数调用
建树和更新的时候都要调用 pushup 来更新父节点内容,更新和查询时都要调用 pushdown 来下传标记
6. pushdown 函数里面
注意,pushdown 函数里面调用的不是 pushdown 函数它自己本身,而是 addtag(或者 multag 等)函数。这个蒟蒻无论是刚学还是现在都很容易不动脑子的写错QAQ
三、代码
//总体流程:建树——>更新——>查询
//需要的函数:build ,update ,query ,pushup ,addtag ,pushdown
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
const int T=N*4+5;//记得开四倍空间
int tree[N],a[N],n,tag[N];
void pushup(int cur){//合并信息
tree[cur]=tree[cur<<1]+tree[cur<<1|1];
}
void addtag(int cur,int lt,int rt,int val){
tag[cur]+=val;//更新标记
tree[cur]+=val*(rt-lt+1);//这个区间内要增加的数字为区间长度乘以加上的数
}
void pushdown(int cur,int lt,int rt){//下传标记
if(tag[cur]==0) return;//如果根本就没有标记就返回
int mid=(lt+rt)>>1;
addtag(cur<<1,lt,mid,tag[cur]);//下传给左孩子
addtag(cur<<1|1,mid+1,rt,tag[cur]);//下传给右孩子
tag[cur]=0;//清零现在节点的标记(因为已经下传了不是吗)
}
void build(int cur,int lt,int rt){
if(lt==rt){//当左边界点与右边界点相等时,表示这个点是叶子节点
tree[cur]=a[lt];return;//叶子节点的权值就等于它自己本身
}
int mid=(lt+rt)>>1;
build(cur<<1,lt,mid);//访问左孩子节点
build(cur<<1|1,mid+1,rt);//访问右孩子节点
pushup(cur);//将孩子的信息合并到父节点上
}
void update(int cur,int lt,int rt,int qx,int qy,int val){
if(lt>qy||rt<qx) return;//如果跟现在访问到的区间根本没关系
if(lt>=qx&&rt<=qy){//如果好巧不巧的现在访问的区间都在要更新的区间内
addtag(cur,lt,rt,val);return;//啊这里是懒标记,一个优化,等会再讲
}
pushdown(cur,lt,rt);//先把现在的更新了再说
int mid=(lt+rt)>>1;
update(cur<<1,lt,mid,qx,qy,val);//访问左孩子
update(cur<<1|1,mid+1,rt,qx,qy,val);//访问右孩子
pushup(cur);//更新信息
}
int query(int cur,int lt,int rt,int qx,int qy){//cur是当前查询节点的编号,lt和rt是当前访问到的区间,qx和qy是要查询的区间
if(lt>qy||rt<qx) return 0;//这里的含义可以见update函数
if(lt>=qx&&rt<=qy){
return tree[cur];
}
pushdown(cur,lt,rt);//查询前先更新
int mid=(lt+rt)>>1;
return query(cur<<1,lt,mid,qx,qy)+query(cur<<1|1,mid+1,rt,qx,qy);
}
signed main(){
ios::sync_with_stdio(false);
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
build(1,1,n);//记得建树
while(m--){
int opt,x,y,val;
cin>>opt>>x>>y;
if(opt==1){
cin>>val;
update(1,1,n,x,y,val);//更新
}
else{
cout<<query(1,1,n,x,y)<<"\n";//询问
}
}
return 0;//完结散花!
}
四、时间复杂度
| 操作 | 时间复杂度 |
|---|---|
| 建树 | O(n) |
| 更改 | O(log n) |
| 查询 | O(log n) |
五、例题
• 数学计算
Problem
Solve
首先不难想到一种暴力的想法,直接存储每一次更改 x 的值,按照题目模拟即可
但这样肯定会超时,我们不妨观察一下样例,发现无论是操作 1 还是操作 2,最后只有一个数会对 x 的值产生影响
我们不妨将每次乘的数定义为叶子节点。如果是操作 1,就将当前操作的点的值更改为要乘的值;如果是操作 2,就将第 pos 次点的值更改为 1。
由于 x 初始值为 1,每次输出的时候只要将所有叶子节点的值相乘,也就是线段树根节点的值。
Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
int mod;
int tree[N<<2];
void pushup(int cur){
tree[cur]=(tree[cur<<1]*tree[cur<<1|1])%mod;
}
void build(int cur,int lt,int rt){
if(lt==rt){
tree[cur]=1;
return;
}
int mid=(lt+rt)>>1;
build(cur<<1,lt,mid);
build(cur<<1|1,mid+1,rt);
pushup(cur);
}
void update(int cur,int lt,int rt,int qx,int k){
if(lt>qx||rt<qx) return;
if(lt==qx&&rt==qx){
tree[cur]=k%mod;
return;
}
int mid=(lt+rt)>>1;
update(cur<<1,lt,mid,qx,k);
update(cur<<1|1,mid+1,rt,qx,k);
pushup(cur);
}
signed main(){
ios::sync_with_stdio(false);
int t;
cin>>t;
while(t--){
memset(tree,0,sizeof(tree));
int n;
cin>>n>>mod;
build(1,1,n);
for(int i=1;i<=n;i++){
int type,x;
cin>>type>>x;
if(type==1) update(1,1,n,i,x);
else update(1,1,n,x,1);
cout<<tree[1]<<"\n";
}
}
return 0;
}
• 上帝造题的七分钟 2 / 花神游历各国
Problem
Solve
看到根号,差点以为不能直接暴力去更新
但其实暴力更新后,加上一个小优化是能过这道题的
首先我们不难发现,\(\sqrt{1}=1\)
题目里的要求是向下取整,所以我们可以将上面那个显而易见的结论推广一下:
如果有一段区间里的最大值是 1,那么对这段区间开根后值依然不变
再加上普通的线段树操作,这道题就可以过了
Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
int n,a[N];
int tree[N<<2];
int maxi[N<<2];
void pushup(int cur){
tree[cur]=tree[cur<<1]+tree[cur<<1|1];
maxi[cur]=max(maxi[cur<<1],maxi[cur<<1|1]);
}
void build(int cur,int lt,int rt){
if(lt==rt){
tree[cur]=maxi[cur]=a[lt];
return;
}
int mid=(lt+rt)>>1;
build(cur<<1,lt,mid);
build(cur<<1|1,mid+1,rt);
pushup(cur);
}
void update(int cur,int lt,int rt,int qx,int qy){
if(lt>qy||rt<qx) return;
if(lt>=qx&&rt<=qy&&maxi[cur]==1) return;
if(lt==rt&<>=qx&<<=qy){
tree[cur]=maxi[cur]=sqrt(tree[cur]);
return;
}
int mid=(lt+rt)>>1;
update(cur<<1,lt,mid,qx,qy);
update(cur<<1|1,mid+1,rt,qx,qy);
pushup(cur);
}
int query(int cur,int lt,int rt,int qx,int qy){
if(lt>qy||rt<qx) return 0;
if(lt>=qx&&rt<=qy) return tree[cur];
int mid=(lt+rt)>>1;
return query(cur<<1,lt,mid,qx,qy)+query(cur<<1|1,mid+1,rt,qx,qy);
}
signed main(){
ios::sync_with_stdio(false);
int q;
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
build(1,1,n);
cin>>q;
while(q--){
int type,x,y;
cin>>type>>x>>y;
if(x>y) swap(x,y);
if(type==0) update(1,1,n,x,y);
else cout<<query(1,1,n,x,y)<<"\n";
}
return 0;
}
• 奇怪的计算器
Problem
Solve
将输入的每一个查询的数都看做一个节点,建树维护最小值和最大值,进行区间修改操作。每操作完一次后查找第一个比 l 小的点设为 x ,第一个比 r 大的点设为 y ,区间赋值 [1,x] 为 l ,[y,n]为 r 。
其实这道题只需要打标记就行了,值得注意的是 pushdown 的顺序,应该是先 set ,再 mul ,然后 add ,最后是操作四的标记数组
Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
int mini[N<<2],maxi[N<<2],tag_plus[N<<2],tag_mul[N<<2],tag_stran[N<<2],tag_set[N<<2];
struct node{
char c;int num;
}ope[N];
struct Node{
int num,id,tree;
}a[N];
inline void pushup(int cur){
mini[cur]=min(mini[cur<<1],mini[cur<<1|1]);
maxi[cur]=max(maxi[cur<<1],maxi[cur<<1|1]);
}
inline void addtag_plus(int cur,int val){
mini[cur]+=val;
maxi[cur]+=val;
tag_plus[cur]+=val;
}
inline void addtag_mul(int cur,int val){
mini[cur]*=val;
maxi[cur]*=val;
tag_mul[cur]*=val;
tag_plus[cur]*=val;
tag_stran[cur]*=val;
}
inline void addtag_set(int cur,int val){
mini[cur]=maxi[cur]=val;
tag_plus[cur]=tag_stran[cur]=0;
tag_mul[cur]=1;
tag_set[cur]=val;
}
inline void addtag_stran(int cur,int lt,int rt,int val){
mini[cur]+=a[lt].num*val;
maxi[cur]+=a[rt].num*val;
tag_stran[cur]+=val;
}
inline void pushdown_plus(int cur,int lt,int rt){
if(tag_plus[cur]==0) return;
int mid=(lt+rt)>>1;
addtag_plus(cur<<1,tag_plus[cur]);
addtag_plus(cur<<1|1,tag_plus[cur]);
tag_plus[cur]=0;
}
inline void pushdown_mul(int cur,int lt,int rt){
if(tag_mul[cur]==1) return;
int mid=(lt+rt)>>1;
addtag_mul(cur<<1,tag_mul[cur]);
addtag_mul(cur<<1|1,tag_mul[cur]);
tag_mul[cur]=1;
}
inline void pushdown_set(int cur,int lt,int rt){
if(tag_set[cur]==0) return;
int mid=(lt+rt)>>1;
addtag_set(cur<<1,tag_set[cur]);
addtag_set(cur<<1|1,tag_set[cur]);
tag_set[cur]=0;
}
inline void pushdown_stran(int cur,int lt,int rt){
if(tag_stran[cur]==0) return;
int mid=(lt+rt)>>1;
addtag_stran(cur<<1,lt,mid,tag_stran[cur]);
addtag_stran(cur<<1|1,mid+1,rt,tag_stran[cur]);
tag_stran[cur]=0;
}
inline void build(int cur,int lt,int rt){
tag_mul[cur]=1;
if(lt==rt){
mini[cur]=maxi[cur]=a[lt].num;
return;
}
int mid=(lt+rt)>>1;
build(cur<<1,lt,mid);
build(cur<<1|1,mid+1,rt);
pushup(cur);
}
inline void addtag_min(int cur,int lt,int rt,int l){
if(maxi[cur]<l){
addtag_set(cur,l);
return;
}
if(lt==rt) return;
pushdown_set(cur,lt,rt);
pushdown_mul(cur,lt,rt);
pushdown_plus(cur,lt,rt);
pushdown_stran(cur,lt,rt);
int mid=(lt+rt)>>1;
addtag_min(cur<<1,lt,mid,l);
if(mini[cur<<1|1]<l) addtag_min(cur<<1|1,mid+1,rt,l);
pushup(cur);
}
inline void addtag_max(int cur,int lt,int rt,int r){
if(mini[cur]>r){
addtag_set(cur,r);
return;
}
if(lt==rt) return ;
pushdown_set(cur,lt,rt);
pushdown_mul(cur,lt,rt);
pushdown_plus(cur,lt,rt);
pushdown_stran(cur,lt,rt);
int mid=(lt+rt)>>1;
if(maxi[cur<<1]>r) addtag_max(cur<<1,lt,mid,r);
addtag_max(cur<<1|1,mid+1,rt,r);
pushup(cur);
}
inline void queryy(int cur,int lt,int rt){
if(lt==rt){
a[lt].tree=mini[cur];
return;
}
pushdown_set(cur,lt,rt);
pushdown_mul(cur,lt,rt);
pushdown_plus(cur,lt,rt);
pushdown_stran(cur,lt,rt);
int mid=(lt+rt)>>1;
queryy(cur<<1,lt,mid);
queryy(cur<<1|1,mid+1,rt);
}
inline bool cmp(Node x,Node y){return x.num<y.num;}
inline bool cmpp(Node x,Node y){return x.id<y.id;}
signed main(){
// freopen("10.in","r",stdin);
// freopen("10.out","w",stdout);
ios::sync_with_stdio(false);
int n,l,r,q;
cin>>n>>l>>r;
for(int i=1;i<=n;i++) cin>>ope[i].c>>ope[i].num;
cin>>q;
for(int i=1;i<=q;i++){
cin>>a[i].num;
a[i].id=i;
}
sort(a+1,a+q+1,cmp);
build(1,1,q);
for(int i=1;i<=n;i++){
char c=ope[i].c;
int num=ope[i].num;
if(c=='+'){
addtag_plus(1,num);
}
if(c=='-'){
addtag_plus(1,-num);
}
if(c=='*'){
addtag_mul(1,num);
}
if(c=='@'){
addtag_stran(1,1,q,num);
}
addtag_min(1,1,q,l);
addtag_max(1,1,q,r);
}
queryy(1,1,q);
sort(a+1,a+q+1,cmpp);
for(int i=1;i<=q;i++) cout<<a[i].tree<<"\n";
return 0;
}
-
更多的题目


 浙公网安备 33010602011771号
浙公网安备 33010602011771号