哈希表概念

 

问题:

在内存中用数组存储50000个单词,用数组下标去找单词很快,但我们在单词软件中不知道单词在数组中的下标.

如a的下标为0,z最后单词的下标为49999,如果以这种方式来找的话，那么查找z开头的单词速度就会相当的慢。

方案:

想一个方法快速的找到单词相对应的下标,哈希函数的定义

将数据元素的关键字K作为自变量，通过一定的函数关系（称为哈希函数），计算出的值，即为该元素的存储地址

即其本身还是一个数组,只不过通过一个算法快速的找到其下标地址而已.

哈希函数的冲突

当用哈希函数新增元素时,算出来该元素的存储地址若已经存有元素的话,那么就称之为冲突,那么就得想办法来避免这种冲突.

示例

下面来看一个实际的例子.只做演示

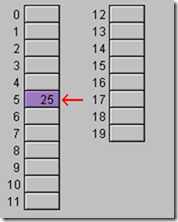
以一个元素为20个的数组为例子

1.哈希函数

取数组大小的余数,即5%20和25%20是相同的.

2.插入25,余数为5

所以其存储地址为5

3.插入5

由于插入5时,与25的存储地址发生了冲突,就需要处理,这里使用了开发地址法的线性探测方法

线性探测

即若遇到地址发生了冲突,则沿着数组的下标继续寻找空白单元

查找

如查找25,算出来的存储地址为5,马上就能找到,即实现了1次查找，删除操作与查找相同,找到以后赋空值就可

实现

public class IntHashTable
{
    private int[] items;

    public IntHashTable(int size)
    {
        items = new int[size];
        for (int i = 0; i < items.Length; i++)
        {
            items[i] = -1;
        }
    }


    private int hashFunc(int key)
    {
        return key % items.Length;
    }

    public void Insert(int item)
    {
        int hashVal = hashFunc(item);
        while (items[hashVal]!=-1)
        {
            hashVal++;
        }
        items[hashVal] = item;
    }

    public int Find(int key)
    {
        int hashVal = hashFunc(key);
        while (items[hashVal]!=-1)
        {
            if (items[hashVal] == key)
                return hashVal;
            hashVal++;
            hashVal = hashFunc(hashVal);
        }
        return -1;
    }

    public void Delete(int key)
    {
        int hashVal = hashFunc(key);
        while (items[hashVal] != -1)
        {
            if (items[hashVal] == key)
            {
                items[hashVal] = -1;
            }
            hashVal++;
            hashVal = hashFunc(hashVal);
        }
    }

    public static void Main()
    {
        IntHashTable ht = new IntHashTable(20);

        ht.Insert(11);
        ht.Insert(12);
        ht.Insert(32);
        ht.Find(32);
        ht.Delete(32);
    }
}

链地址法

将发生冲突的存在一个链表里面,并且保持链表有序.如下

public class Link
{
    public int Value { get; set; }

    public Link Next { get; set; }
}

class SortedList
{
    private Link first;

    public SortedList()
    { 
        first = null;
    }

    public void Insert(Link theLink)
    {
        int key = theLink.Value;
        Link previous = null;
        Link current = first;

        while (current != null && key > current.Value)
        {
            previous = current;
            current = current.Next;
        }
        if (previous == null)
            first = theLink;
        else
            previous.Next = theLink;
        theLink.Next = current;
    }

    public void Delete(int key)
    {
        Link previous = null;
        Link current = first;

        while (current != null && key != current.Value)
        {
            previous = current;
            current = current.Next;
        }

        if (previous == null)
            first = first.Next;
        else
            previous.Next = current.Next;
    }

    public Link Find(int key)
    {
        Link current = first;

        while (current != null && current.Value <= key)
        {
            if (current.Value == key)
                return current;
            current = current.Next;
        }
        return null;
    }
}

public class LinkHashTable
{
    private SortedList[] items;

     public LinkHashTable(int size)
    {
        items = new SortedList[size];
        for (int i = 0; i < items.Length; i++)
        {
            items[i] = new SortedList();
        }
    }


    private int hashFunc(int key)
    {
        return key % items.Length;
    }

    public void Insert(int item)
    {
        int hashVal = hashFunc(item);
        var link = items[hashVal];
        link.Insert(new Link() { Value = item });
    }

    public int Find(int key)
    {
        int hashVal = hashFunc(key);
        var link = items[hashVal];
        return link.Find(key).Value;
        return -1;
    }

    public void Delete(int key)
    {
        int hashVal = hashFunc(key);
        var link = items[hashVal];
        link.Delete(key);
    }
}

二次探测

当发生冲突时才进行探测,犹如人左右张望,先看右边有无空位，再看左边有无空位,即先确认左右,

如上图的最后一个关键字3,

3和47冲突,先找到4(97)又发生冲突则找左边2空位.

遵照哈希函数公式即可