红黑树操作

红黑树规则

1. 每一个节点不是红色就是黑色的
2. 根总是黑色的
3. 如果节点是红色的,则它的子节点必须是黑色的(节点是黑色，子节点也可以为红色/黑色)
4. 从根到叶节点或空子节点的每条路径，必须包含相同数目的黑色节点

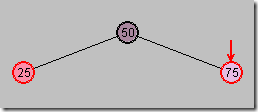
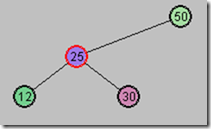
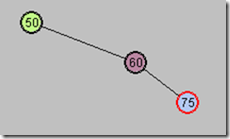
试验1：插入两个红色节点

图1

试验2：旋转

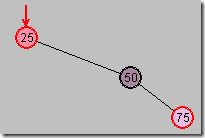
1.向右旋转

图2

开始时如图1
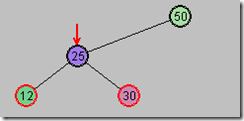
选中50，向右旋转

1. 父节点移到其右子节点位置
2. 左节点上移
3. 右节点下移

树变成非平衡的，违背了规则2

选中25，向左旋转则恢复图1的位置

试验3：颜色变换

开始时如图1
现在再插入一个数时(无法插入),因为违背了规则3,红色节点的子节点不可以为红色,所以需要把红色节点先变成黑色

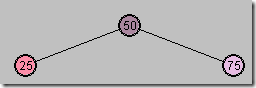
(1)现在三个节点都是黑色了

图3

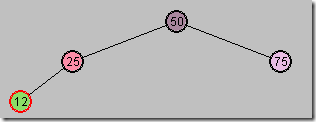
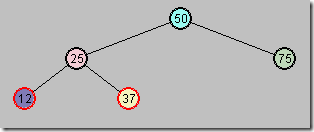
(2)插入节点

图4

这样就不会违背红黑树规则

试验4：非平衡树

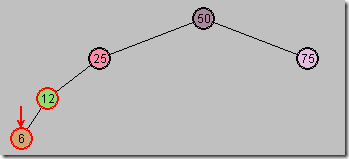
基于图4再次插入1个节点6

图5

现在节点12违背了规则3

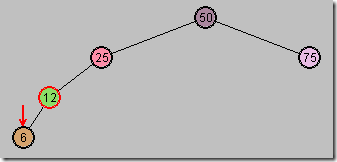
为了修正这个错误,现在变换节点6的颜色

图6

现在规则3修正了,但违背了规则4

黑色高度(从根到指定及诶单路径上的黑色节点数目),根节点到6有3个黑色节点，到75则只有2个

空子节点

如果节点只有左子节点,那么其空缺的右子节点就是空子节点(反之亦然),如图6的右子节点

侧子孙节点

图6

如果节点的父节点与该节点的子节点同一侧,则该节点的子节点为该节点父节点的外侧子孙节点,反之则成为内侧子孙节点

如12是50的外侧子孙节点,37是50的内侧子孙节点

插入过程的颜色转换

(1)当节点为空时,插入一个黑节点,即根节点

(2)当遇到一个有两个红色子节点的黑色节点时,把子节点变为黑色,父节点变为红色(根节点除外)
================>

==================>

组图1

新插入节点可能的位置

 

组图2

 

1. X为新插入的节点(总是红色)
2. X父节点为P
3. P的父节点为G(X的祖父节点)

X,P,G的不同情景

1.是黑色时,就什么事情也不做,如组图2,不管父节点什么颜色都不会违背规则

2.当P是红色,X是G的一个外侧子孙节点

需要做3步来修正规则

1. 改变G(60)的颜色
2. 改变P(75)的颜色
3. 以G为顶,向左旋转

先做前面两步

然后进行左旋转

G节点的右节点上移,G节点本身变为右节点的左节点

反之则左节点上移,本身成为左节点的右节点,如图2

如此树再次平衡

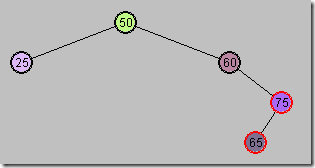
3.当P是红色,X是G的一个内侧子孙节点

与第2种情况差不多，但多了一次旋转,即先将内存子孙节点调整为外侧子孙节点,接着操作就一样了

需要做4来修正规则

1. 改变G(60)的颜色
2. 改变X(65)的颜色
3. 以P为顶,向右旋转
4. 再以G为顶,向左旋转

先做前面两步

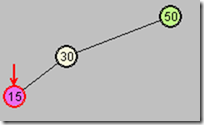
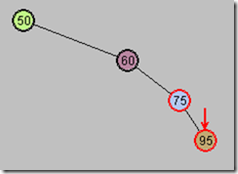
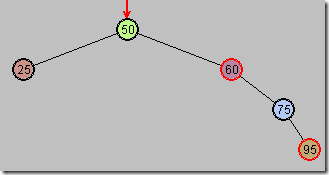
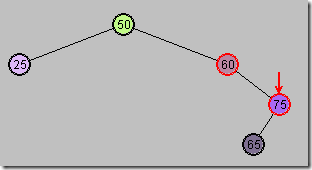
第三步：以P为顶,向右旋转

P(75)下移,X上移,并且P成为X的右子节点

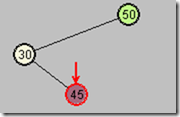
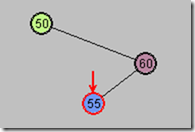
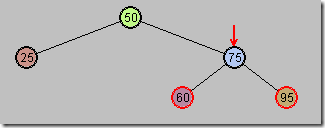
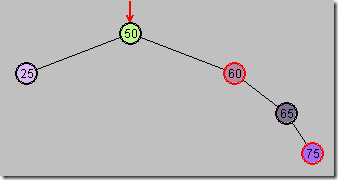
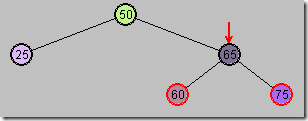
第四步:再以G为顶,向左旋转