区间动态规划-DFS种类数(SOJ 2469)

2469: Exploring Pyramids

问题：给出一棵树我们可以写出它的深搜结果，现在给出深搜结果字符串$S$求解对应树的种类数。

例子：深搜结果:$ABABABA$,对应的树(根结点在底层)有$5$个。

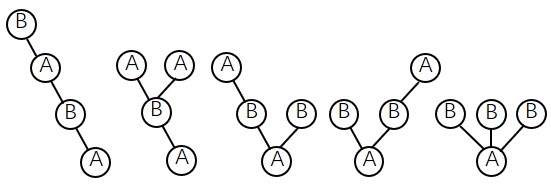
分析：应用区间动态规划，定义$dp[i][j]$为$S[i..j]$对应的树的个数，则分两类：

(1)$S[i]$有一个子结点(上例中前两种情况)，$S[i..j]$对应的树的个数就等于$S[i+1..j-1]$对应的树的个数，前提是$S[i]=S[j]$.即，若$S[i]=S[j]$，则$dp[i][j]=dp[i+1][j-1]$；否则$dp[i][j]=0$.

(2)$S[i]$有$\ge 2$个子结点(上例中后三种情况)。最开始我写的状态转移方程如下：

$dp[i][j]=\sum_{k=i+1}^{j-1}dp[i][k]*dp[k][j]$,

后来发现这样存在重复计算，存在于$dp[k][j]$的$\ge 2$个子结点情况，所以修正为

$dp[i][k]*dp[k][j]-dp[i][k]*(dp[k][j]-dp[k+1][j-1])=dp[i][k]*dp[k+1][j-1]$,

但是注意加一个条件$S[k]=S[j]$.

代码：

 

#include<iostream>
#include<cstring>
using namespace std;
char s[301];
long long dp[301][301];
long long con = 1000000000;
int main()
{
    int i, j, k;
    int len;
    int delta;
    while (~scanf("%s", s))
    {
        len = strlen(s);
        for (i = 0; i < len; i++)
            dp[i][i] = 1;
        for (i = 0; i < len - 1; i++)
            dp[i][i + 1] = 0;
        for (delta = 3; delta <= len; delta++)
            for (i = 0; i <= len - delta; i++)
            {
                j = i + delta - 1;
                if (s[i] == s[j])
                    dp[i][j] = dp[i + 1][j - 1];
                else
                {
                    dp[i][j] = 0;
                    continue;
                }
                for (k = i + 1; k < j - 1; k++)
                    if (s[k] == s[j])
                        dp[i][j] = (dp[i][j] + (dp[i][k] * dp[k + 1][j - 1]) % con) % con;
            }
        printf("%lld\n", dp[0][len - 1]);
    }
    return 0;
}