0-1背包

一. 问题描述

给定n个物品，每个物品有一个重量（也可以看作体积）weight[i]和一个价值value[i], 1≤i≤n。现有一个给定容量m的背包，求解背包里装入的物品价值之和的最大值。

二. 分析

定义dp[i][j]为：背包的容量为j并且放入前i个物品的最大价值。我们对第i个物品分析，存在两种情况：装与不装。如果不装，则dp[i][j]=dp[i-1][j];否则dp[i][j]=dp[i-1][j-weight[i]]+value[i].基于dp[i][j]的定义我们有：

dp[i][j]=max{dp[i-1][j], dp[i-1][j-weight[i]]+value[i]}.

初始化条件：

dp[i][0]=0, dp[0][j]=0.

核心代码如下：

for(i=0;i<n;i++)
    for(j=0;j<m;j++)
    {
        if(j>weight[i])
            dp[i][j]=max(dp[i-1][j-weight[i]]+value[i],dp[i-1][j]);
        else
            dp[i][j]=dp[i-1][j];
    }

迭代过程如下表所示，

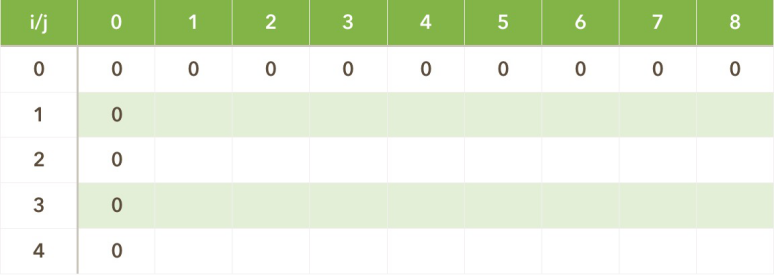
最后输出结果dp[n][m].

三. 优化存储空间

根据状态状态转移方程我们可以看到，第i行的结果只跟第i-1行的结果有关，因此我们只需存储一行结果。只需保留容量这一个状态，状态转移方程如下：

dp[j]=max{dp[j-weight[i]]+value[i], dp[j]}. 

同之前一样，i代表物品序号，j代表可用容量。其实，第一个dp[j]等同于上面的dp[i][j]，dp[j-weight[i]]等同于上面的dp[i-1][j-weight[i]]，第二个dp[j]等同于上面的dp[i-1][j]. 核心代码如下：

memset(dp,0,sizeof(dp)); 
for(i=0;i<n;i++)
    for(j=m;j>=weight[i];j--)
        dp[j]=max(dp[j-weight[i]]+value[i],dp[j]);

这里有两个问题需要解释一下：（1）j为什么是降序；（2）j为什么只到weight[i]而不到0.

上图是二维数组的情况，由于第i行的值只与第i-1行有关，所以事实上我们可以以任意顺序来得到第i行的结果，因为第i行的值之间互不相关。第一段代码中j从0到m，实际上倒过来也是可行的。但是在这里j必须是降序，如果是升序的话，我们可以得到下图的情形

 当我们处理到第[i]个物品时，dp[j]需要dp[j-weight[i]]，我们需要的是i-1时刻的dp[j-weight[i]]，但此时的dp[j-weight[i]]已经是i时刻的了，已经被更新了！这种情况物品i是可以被装多次的！所以我们应该倒着更新dp[j]!

然后是第二个问题，为什么j没有更新从0到weight[i]-1之间的值，这是因为j<weight[i]时，第i个物品装不下，dp[i][j]=dp[i-1][j]也即是dp[j]=dp[j]，dp在[0,weight[i]-1]之间的值不用动了。

Note: 最后解释一下0-1的含义，由于n个物品每个物品只有一个，装或不装，所以称这类问题为0-1背包问题。

参考了以下博文：

http://www.cnblogs.com/aiguona/p/7274222.html