根据两个向量计算它们之间的旋转矩阵
一、简介
本文主要介绍通过给定的两个空间向量,计算出从一个向量旋转到另一个向量的旋转矩阵。
二、步骤
① 假设两个向量分别为vectorBefore(x1,y1,z1), vectorAfter(x2,y2,z2),将这两个向量转为单位向量。
得到 va = normalize(vectorBefore), vb = normalize(vectorAfter)
② vs = vb × va, 叉乘得到旋转轴vs
③ v = normalize(vs), vs转为单位向量得到v
④ ca = vb · va, 点乘得到旋转角的余弦值 ca, 即cos(angle)
⑤ vt = v * scale, 对v进行缩放,方便后面计算, scale = 1 - ca
⑥ 旋转矩阵rm为 [3,3]矩阵, 计算原理为罗德里格旋转公式(Rodrigues' rotation formula)
rm[0,0] = vt.x * v.x + ca
rm[1,1] = vt.y * v.y + ca
rm[2,2] = vt.z * v.z + ca
vt.x *= v.y
vt.z *= v.x
vt.y *= v.z
rm[0,1] = vt.x - vs.z
rm[0,2] = vt.z - vs.y
rm[1,0] = vt.x - vs.z
rm[1,2] = vt.y - vs.x
rm[2,0] = vt.z - vs.y
rm[2,1] = vt.y - vs.x
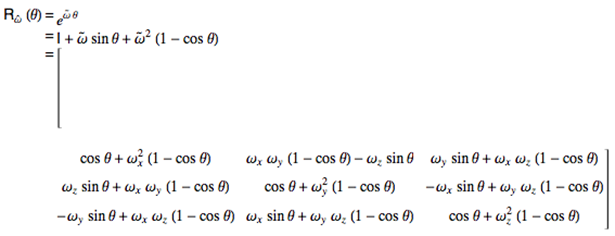
三、效果
红色为旋转前的平面,蓝色为旋转后的实际平面, 绿色是对红色平面应用计算的旋转矩阵后得到的平面,所以绿色与蓝色应在同一平面内。

四、代码
public struct Vec3 { public float x; public float y; public float z; public Vec3(float X, float Y, float Z) { x = X; y = Y; z = Z; } } float[,] getRotationMatrix(Vec3 vectorBefore, Vec3 vectorAfter) { Vec3 vb = Normalize(vectorBefore); Vec3 va = Normalize(vectorAfter); Vec3 vs = CrossProduct(vb, va); Vec3 v = Normalize(vs); float ca = DotProduct(vb, va); float scale = 1 - ca; Vec3 vt = new Vec3(v.x * scale, v.y * scale, v.z * scale); float[,] rotationMatrix = new float[3,3]; rotationMatrix[0, 0] = vt.x * v.x + ca; rotationMatrix[1, 1] = vt.y * v.y + ca; rotationMatrix[2, 2] = vt.z * v.z + ca; vt.x *= v.y; vt.z *= v.x; vt.y *= v.z; rotationMatrix[0, 1] = vt.x - vs.z; rotationMatrix[0, 2] = vt.z + vs.y; rotationMatrix[1, 0] = vt.x + vs.z; rotationMatrix[1, 2] = vt.y - vs.x; rotationMatrix[2, 0] = vt.z - vs.y; rotationMatrix[2, 1] = vt.y + vs.x; return rotationMatrix; } Vec3 CrossProduct(Vec3 a, Vec3 b) { Vec3 c = new Vec3() { x = a.y * b.z - a.z * b.y, y = a.z * b.x - a.x * b.z, z = a.x * b.y - a.y * b.x }; return c; } float DotProduct(Vec3 a, Vec3 b) { return a.x * b.x + a.y * b.y + a.z * b.z; } Vec3 Normalize(Vec3 v) { float frt = (float)Math.Sqrt(v.x * v.x + v.y * v.y + v.z * v.z); if (frt == 0.0f) { return new Vec3(0, 0, 0); } else { return new Vec3(v.x / frt, v.y / frt, v.z / frt); } }
五、调用库
以上是通过自己计算得出结果,其实eigen库中有输入两个向量得出旋转矩阵的接口,非常简单。
Eigen::Matrix3d rotMatrix; Eigen::Vector3d vectorBef(vectorBefore[0], vectorBefore[1], vectorBefore[2]); Eigen::Vector3d vectorAft(vectorAfter[0], vectorAfter[1], vectorAfter[2]); rotMatrix = Eigen::Quaterniond::FromTwoVectors(vectorBef, vectorAft).toRotationMatrix();



 浙公网安备 33010602011771号
浙公网安备 33010602011771号