学习笔记：超级无敌线段树大杂烩
0.前言
本文是一篇线段树大杂烩。
主要内容：
- 普通线段树的构造、修改、查询和应用
- 线段树（权值线段树）的合并和分裂与其应用
- 线段树优化建图与其应用
- 可持久化线段树及其应用
- 线段树分治与其应用
参考资料：
1.线段树概况
线段树，是一类可以在对数复杂度内处理区间型问题的数据结构。
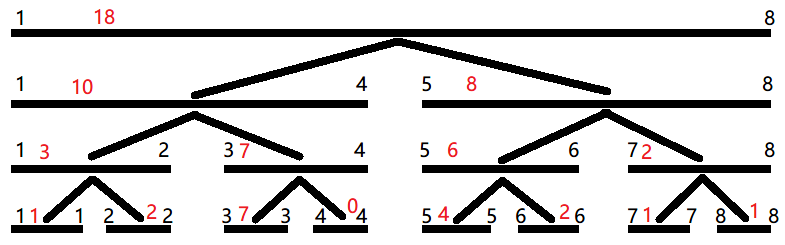
这是一张线段树的图。容易发现，线段树是一棵二叉树，每个节点保存了这个节点管理的区间 \(l,r\)（黑色数字）这个区间的 sum（红色数字）（也可以是 max,min 等等）。
1.1.线段树的构造
在图中，我们发现了线段树的一些特征：一个节点的两个儿子节点分别管理这个节点的一半，一个节点的 sum 值等于两个儿子节点的 sum 值。通过这两个特征，就可以通过递归的方式构造一棵线段树（应该都知道二叉树的简便构造方法吧）。（至于需不需要保存节点的左右范围，我觉得随意。本博文此章节的线段树采用保存左右范围，但是后半部分不保存。主要是这篇文章前后时间差距过大）
CI N = 1e5, N4 = 4e5; int sum[N4 + 5], l[N4 + 5], r[N4 + 5], arr[N + 5]; // 线段树需要开四倍大小
void pushup (int root) {sum[root] = sum[root << 1] + sum[root << 1 | 1];} // 线段树子节点向父亲节点更新
void build (int root, int L, int R) {
l[root] = L; r[root] = R;
if (L == R) {sum[root] = arr[L]; return ;} // 叶子节点
int mid = (L + R) >> 1; build (root << 1, L, mid); build (root << 1 | 1, mid + 1, R);
pushup (root); // 向上更新
}
1.2.区间查单点改
1.2.1.区间查询
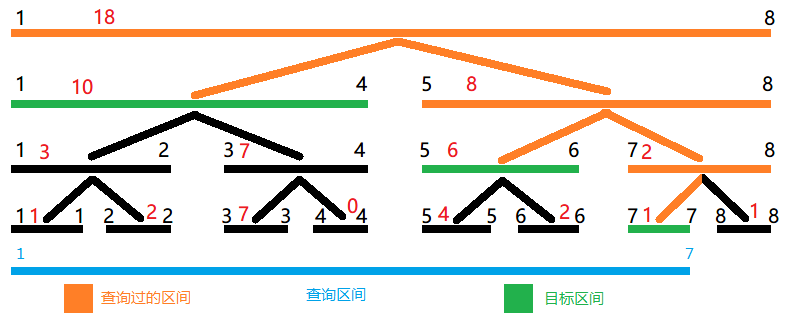
还是上面那棵线段树，如果我们需要查询区间 \([1,7]\) 的和，一种做法当然是从 \([1,1]\) 加到 \([7,7]\)（那你写线段树干嘛）。但是我们发现，从 \([1,1]\) 到 \([4,4]\) 的和就是 \([1,4]\) 的 sum 值。所以 \([1,7]\) 的和就等于 \([1,4],[5,6],[7,7]\) 的和。但是怎么判断查询区间可以分成几个小区间呢？考虑分类，我们从根节点向下递归（因为从上向下递归的，可以保证分割的区间数最少）：如果当前区间包含在查询区间内，那么直接返回该节点 sum 值；如果查询区间与当前区间的左儿子有交集，向左儿子递归；如果右儿子有交集，向右儿子递归。
int Sum (int root, int L, int R) {
if (l[root] >= L && r[root] <= R) return sum[root]; // 查询区间包含当前区间
if (r[root] < L || l[root] > R) return 0; // 无交集
int mid = (l[root] + r[root]) >> 1, s = 0;
if (L <= mid) s += Sum (root << 1, L, R); // 左儿子有交集
if (R > mid) s += Sum (root << 1 | 1, L, R); // 右儿子有交集
return s;
}
1.2.2.单点修改
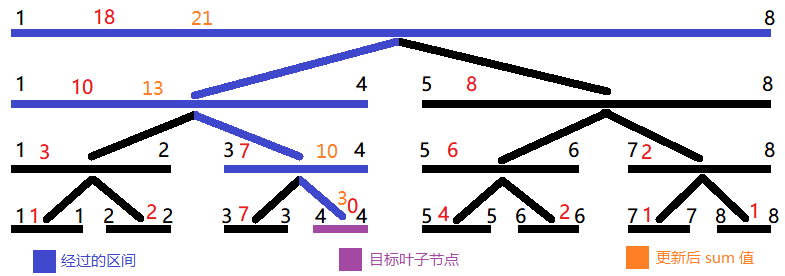
（比区间查询简单多了）只需要找到对应的叶子节点，在递归返回的时候向上更新就好了。
void change (int root, int x, int k) {
if (l[root] == r[root]) {sum[root] += k; return ;} // 到达叶子节点
if (l[root] > x || r[root] < x) return ;
int mid = (l[root] + r[root]) >> 1;
if (x <= mid) change (root << 1, x, k);
else if (x > mid) change (root << 1 | 1, x, k);
pushup (root); // 向上更新
}
1.3.单点查区间改
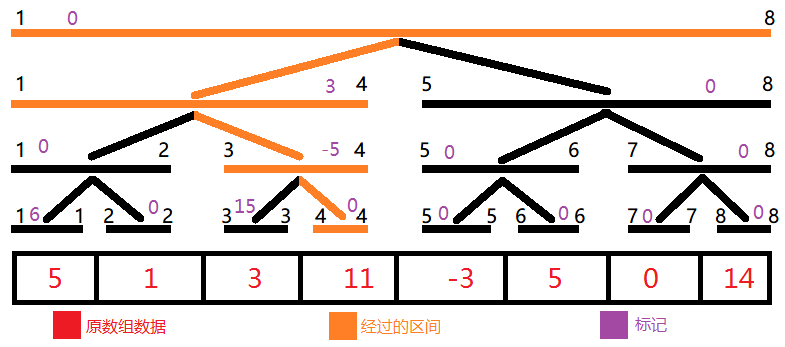
考虑换一种实现方式，我们构造一棵 sum 值全为 0 的线段树。区间修改时把包含的区间加上 \(k\) 的标记，单点查询时把沿路的标记加起来，再加上这个点原本的值即可。
1.4.区间查区间改
此时就不能像之前一样直接查询和修改了，我们考虑增加一个 lazytag：在区间加法的时候，如果次区间包含在被加区间中，那么我们不仅要将 sum 值加上 \(k\times\text{区间大小}\)，还要将该节点的 lazytag 加上 \(k\)，表示它的子树上的节点全部都要加 \(k\)。
然后每次递归到一个节点时，如果这个节点的 lazytag 不为 0，那么我们将 lazytag 下传，保证当前节点的儿子节点以上部分的 sum 值是正确的。
如何下传 lazytag 呢？首先将该节点的儿子节点的 lazytag 加上 \(k\)，再将儿子节点的 sum 值加上 \(\text{该节点的 lazytag 值}\times\text{儿子节点的范围}\) ，最后将该节点的 lazytag 置为 0 即可。
注意：在区间修改和区间查询时都需要进行下传操作。
code
void pushup (int root) {sum[root] = sum[root << 1] + sum[root << 1 | 1];}
void pushdown (int root, int L, int R) {
if (lz[root] == 0) return ; lz[root << 1] += lz[root]; lz[root << 1 | 1] += lz[root]; int mid = (L + R) >> 1; // 下传 lazytag
sum[root << 1] += lz[root] * (mid - L + 1); sum[root << 1 | 1] += lz[root] * (R - mid); lz[root] = 0; // 更新 sum
}
void add (int root, int L, int R, int x, int y, int k) {
if (L >= x && R <= y) {sum[root] += k * (R - L + 1); lz[root] += k; return ;} int mid = (L + R) >> 1; pushdown (root, L, R);
if (x <= mid) add (root << 1, L, mid, x, y, k); if (y > mid) add (root << 1 | 1, mid + 1, R, x, y, k); pushup (root);
}
int query (int root, int L, int R, int x, int y) {
if (L >= x && R <= y) return sum[root]; int mid = (L + R) >> 1, s = 0; pushdown (root, L, R);
if (x <= mid) s += query (root << 1, L, mid, x, y); if (y > mid) s += query (root << 1 | 1, mid + 1, R, x, y); return s;
}
1.5.维护区间最大子段和
考虑维护四个元素：区间和（sum），区间最大前缀和（pre），区间最大后缀和（nxt），区间最大子段和（ans）。接下来我们分别考虑每个如何维护：
区间和
emmm，就这样维护。
区间最大前缀和
对于一个区间，它的区间最大前缀和有两种可能：
- 超过中间：\(sum_{\text{左儿子}}+pre_{\text{右儿子}}\)
- 没超过中间：\(pre_{\text{左儿子}}\)
取 max 即可。
区间最大后缀和
类似与区间最大前缀和，取 \(sum_{\text{右儿子}}+nxt_{\text{左儿子}}\) 和 \(nxt_{右儿子}\) 的 max 即可。
区间最大子段和
分三类：
- 在左儿子：\(ans_{\text{左儿子}}\)
- 在右儿子：\(ans_{\text{右儿子}}\)
- 跨过中间：\(nxt_{\text{左儿子}}+pre_{\text{右儿子}}\)
取 max。
例题：SP1043 GSS1 - Can you answer these queries I
模板。
code
点击查看代码
#include <bits/stdc++.h>
#define Tp template<typename Ty>
#define Ts template<typename Ty,typename... Ar>
#define ll long long
#define CI const int
#define RI int
#define W while
#define gc getchar
#define ID(x) ((x)<=sm?id1[x]:id2[m/(x)])
#define max(x,y) ((x)>(y)?(x):(y))
#define min(x,y) ((x)<(y)?(x):(y))
#define ms(a,x) memset((a),(x),sizeof(a))
using namespace std;
namespace SlowIO {
void readc (char& c) {W (isspace (c = gc ()));}
Tp void read (Ty& x) {char c; int f = 1; x = 0; W (! isdigit (c = gc ())) f = c ^ '-' ? 1 : -1; W (x = (x * 10) + (c ^ 48), isdigit (c = gc ())); x *= f;}
Ts void read (Ty& x, Ar&... y) {read (x); read (y...);}
} using namespace SlowIO;
CI N = 5e4, N4 = 2e5, INF = 0x3f3f3f3f; int n, m, arr[N + 5];
namespace LineTree {
struct node {int sum; int pre; int nxt; int ans; node () {sum = 0; pre = nxt = ans = -INF;}} a[N4 + 5];
node merge (node x, node y) {
node res; res.sum = x.sum + y.sum; res.pre = max (x.pre, x.sum + y.pre); res.nxt = max (y.nxt, y.sum + x.nxt); res.ans = max (max (x.ans, y.ans), x.nxt + y.pre);
return res;
}
void build (int root, int L, int R) {
if (L == R) {a[root].sum = a[root].pre = a[root].nxt = a[root].ans = arr[L]; return ;} int mid = (L + R) >> 1;
build (root << 1, L, mid); build (root << 1 | 1, mid + 1, R); a[root] = merge (a[root << 1], a[root << 1 | 1]);
}
node query (int root, int L, int R, int x, int y) {
if (L >= x && R <= y) return a[root]; int mid = (L + R) >> 1; node l, r;
if (x <= mid) l = query (root << 1, L, mid, x, y); if (y > mid) r = query (root << 1 | 1, mid + 1, R, x, y);
return merge (l, r);
}
} using namespace LineTree;
int main () {
RI i, j; for (read (n), i = 1; i <= n; ++ i) read (arr[i]); build (1, 1, n); read (m); W (m --) {
int l, r; read (l, r); printf ("%d\n", query (1, 1, n, l, r).ans);
}
return 0;
}
2.线段树合并
权值线段树：权值线段树像桶一样，每个叶节点保存的是数字的个数，而不是数字本身。
动态开点线段树：指线段树上的节点有需要时再创建，而不像一般的线段树，建树时创建好所有的节点，所以一个节点的左右儿子需要额外存储其 id。
线段树合并，一般指权值线段树的合并。步骤非常的简单（我使用的是带返回值的合并）（两棵树的节点分别为A，B）
- 如果不是叶子节点，则将 B 的左儿子合并至 A 的左儿子，B 的右儿子合并至 A 的右儿子，最后 pushup 后返回 A 即可。
- 如果 A 为空或 B 为空（因为两棵权值线段树不一定是满的（因为是动态开点）），则返回另一个即可。
- 如果是叶子节点，则将 B 的信息合并到（如何合并看情况）A上，返回 A 即可。
code
int merge (int a, int b, int L, int R) {
if (! a || ! b) return a + b/*显然，如果一个是 0，加起来后就是另一个*/; if (L == R) {/*将 b 的信息并到 a 上，这里看情况*/return a;} int mid = (L + R) >> 1;
sl[a] = merge (sl[a], sl[b], L, mid); sr[a] = merge (sr[a], sr[b], mid + 1, R); pushup (a); return a;
}
当然，既然是线段树，单点修改不能少，给出动态开点权值线段树的单点加：
void update (int &root, int L, int R, int pos, int v) { // 加入 v 个 pos
if (! root) root = ++ ntot; if (L == R) {sum[root] += v; return ;} int mid = (L + R) >> 1;
if (pos <= mid) update (sl[root], L, mid, pos, v); else update (sr[root], mid + 1, R, pos, v); pushup (root);
}
2.1.例题
一堆例题
- CF600E Lomsat gelral 题解
- P3224 [HNOI2012]永无乡 题解
- P3521 [POI2011]ROT-Tree Rotations 题解
- P3605 [USACO17JAN]Promotion Counting P 题解
- P4556 [Vani有约会]雨天的尾巴 /【模板】线段树合并 题解
3.线段树分裂
线段树分裂可以将一颗线段树中一段范围中的值分裂到另一颗线段树上。在实现上：
我们新开一颗线段树，然后在原线段树上递归找出在指定范围中的线段，递归寻找时新线段树和它同步向左右儿子递归。到达在指定范围的线段时，将信息赋值到新线段树相同位置的线段，并清空原线段树的这条线段即可。
code
void split (int &a, int &b, int L, int R, int x, int y) {
if (! a) return ; if (L >= x && R <= y) {b = a; a = 0; return ;} if (! b) b = ++ ntot; int mid = (L + R) >> 1;
if (x <= mid) split (sl[a], sl[b], L, mid, x, y); if (y > mid) split (sr[a], sr[b], mid + 1, R, x, y); pushup (a); pushup (b);
}
3.1.例题
4.线段树优化建图
当一个点要向一个区间内的点连边或者一个区间内的点向一个点连边时，我们可以 \(\mathcal{O}(n)\) 建边，但是如果我们使用线段树优化，复杂度可以降到 \(\mathcal{O}(\log n)\)。
我们考虑建两颗线段树，一颗外向树和一颗内向树。线段树的叶子节点对应原图中的点，其余的点用来管理区间。
对于一个点要向一个区间内的点连边，我们考虑线段树的区间修改，找到在外向线段树区间内的节点，将这个点和这些节点连边，外向线段树将连通性向下传递，就可以连接点和区间（如图）：
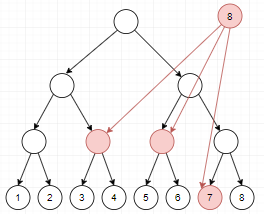
对于一个区间内的点向一个点同理，将内向线段树中对应的节点向这个点连边：
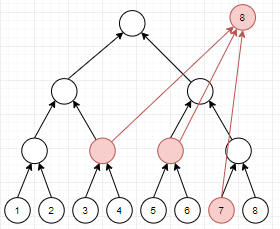
需要注意的是，内向线段树和外向线段树的叶子节点其实是同一个点，所以要在它们之间连边权为 \(0\) 的边：
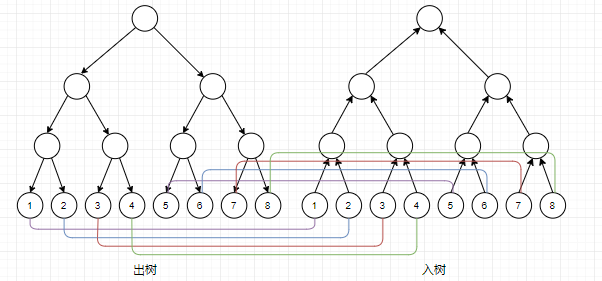
然后图就建好了，接下来可以最短路或者别的。
code
namespace LineTree {
int arr[N + 5];
void build (int root, int L, int R) {
if (L == R) {arr[L] = root; return ;} int mid = (L + R) >> 1; add (root, root << 1, 0); add (root, root << 1 | 1, 0);
add ((root << 1) + K, root + K, 0); add ((root << 1 | 1) + K, root + K, 0); build (root << 1, L, mid); build (root << 1 | 1, mid + 1, R);
}
void addin (int root, int L, int R, int pos, int v, int x, int y) {
if (L >= x && R <= y) {add (pos + K, root, v); return ;} int mid = (L + R) >> 1;
if (x <= mid) addin (root << 1, L, mid, pos, v, x, y); if (y > mid) addin (root << 1 | 1, mid + 1, R, pos, v, x, y);
}
void addout (int root, int L, int R, int pos, int v, int x, int y) {
if (L >= x && R <= y) {add (root + K, pos, v); return ;} int mid = (L + R) >> 1;
if (x <= mid) addout (root << 1, L, mid, pos, v, x, y); if (y > mid) addout (root << 1 | 1, mid + 1, R, pos, v, x, y);
}
} using namespace LineTree;
4.1.例题
5.可持久化线段树（主席树）
假设我们操作一次就经过一个时刻，我们现在需要访问某时刻下的线段树（就是历史版本的线段树）。
朴素做法显然是每一次操作后都将线段树复制一份，但是这样时空复杂度都太大了。
不难发现，当我们做一次单点修改后，线段树中实际只有从根节点到目标节点这条链中的 \(\log n\) 个点有变化，所以实际上我只需要多开 \(\log n\) 个点保存新的链，并将它挂到原来的线段树上即可，如图：
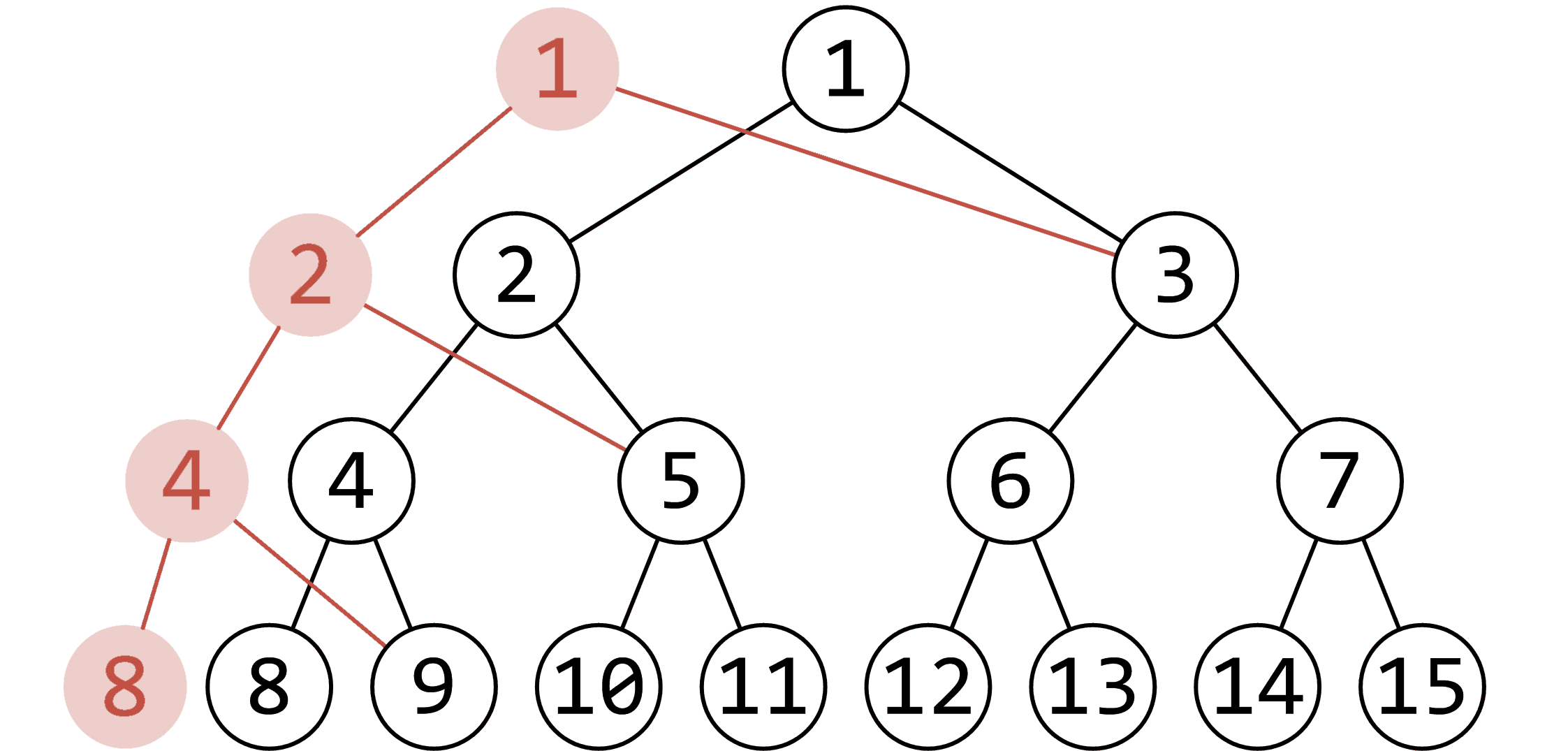
例题：P3919 【模板】可持久化线段树 1（可持久化数组）
code：
int val[N4 + 5], sl[N4 + 5], sr[N4 + 5], rt[N + 5], ntot = 0;
void build (int &root, int L, int R) {
root = ++ ntot; if (L == R) {val[root] = arr[L]; return ;} int mid = (L + R) >> 1;
build (sl[root], L, mid); build (sr[root], mid + 1, R);
}
void add (int &root, int lst, int L, int R, int pos, int v) {
root = ++ ntot; sl[root] = sl[lst]; sr[root] = sr[lst]; val[root] = val[lst]; if (L == R) {val[root] = v; return ;} int mid = (L + R) >> 1;
if (pos <= mid) add (sl[root], sl[lst], L, mid, pos, v); else add (sr[root], sr[lst], mid + 1, R, pos, v);
}
int query (int root, int L, int R, int pos) {
if (L == R) return val[root]; int mid = (L + R) >> 1;
if (pos <= mid) return query (sl[root], L, mid, pos); else return query (sr[root], mid + 1, R, pos);
}
